Να εξεταστεί αν υπάρχει σταθερά
 τέτοια ώστε η τιμή της
τέτοια ώστε η τιμή της  να 'ναι πρώτος για κάθε
να 'ναι πρώτος για κάθε  .
.Συντονιστής: nkatsipis
 τέτοια ώστε η τιμή της
τέτοια ώστε η τιμή της  να 'ναι πρώτος για κάθε
να 'ναι πρώτος για κάθε  .
.
 ;
;  αντί
αντί  με την απάντηση να είναι θετική. Βασίζεται στο γεγονός ότι πάντα υπάρχει πρώτος μεταξύ των
με την απάντηση να είναι θετική. Βασίζεται στο γεγονός ότι πάντα υπάρχει πρώτος μεταξύ των  και
και  . Για να αντικατασταθεί το
. Για να αντικατασταθεί το  με
με  σε αυτήν την απόδειξη θα πρέπει να γνωρίζουμε ότι πάντα υπάρχει πρώτος μεταξύ των
σε αυτήν την απόδειξη θα πρέπει να γνωρίζουμε ότι πάντα υπάρχει πρώτος μεταξύ των  και
και  το οποίο προς το παρόν είναι εικασία.
το οποίο προς το παρόν είναι εικασία. με
με  . Θα θελα να δω ένα επιχείρημα με τη παραπλήσια.
. Θα θελα να δω ένα επιχείρημα με τη παραπλήσια.
Νομίζω ότι και αυτό είναι εικασία. Έπεται από την Εικασία του Riemann, αλλά έχει αποδειχθεί μόνο για αρκετά μεγάλαDemetres έγραψε:
... πάντα υπάρχει πρώτος μεταξύ τωνκαι
.
 . Δείτε π.χ. εδώ. Αυτό αρκεί για την απόδειξη της ύπαρξης της σταθεράς
. Δείτε π.χ. εδώ. Αυτό αρκεί για την απόδειξη της ύπαρξης της σταθεράς  (που αναφέρεται στη βιβλιογραφία ως σταθερά του Mills).
(που αναφέρεται στη βιβλιογραφία ως σταθερά του Mills). τέτοιο ώστε
τέτοιο ώστε 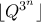 να 'ναι πρώτος για κάθε
να 'ναι πρώτος για κάθε  . Μήπως θέλει κάποιος να τη γράψει;
. Μήπως θέλει κάποιος να τη γράψει;
 είναι ο
είναι ο  -οστός πρώτος τότε
-οστός πρώτος τότε  όπου
όπου  ένας σταθερός θετικός ακέραιος.
ένας σταθερός θετικός ακέραιος. -οστό πρώτο αριθμό για τις διάφορες τιμές του
-οστό πρώτο αριθμό για τις διάφορες τιμές του  (υπάρχουν πολλοί κλειστοί ΚΑΙ αναδρομικοί τύποι σε αντίθεση με αυτό που γράφει το σχολικό βιβλίο στην Α Λυκείου στο εισαγωγικό κεφάλαιο των ακολουθιών ότι τέτοιοι τύποι δεν υπάρχουν. Είχα στείλει έγγραφο στο Υπουργείο πριν χρόνια - όταν ακόμη το κεφάλαιο των προόδων ήταν στη Β Λυκείου - για να κάνουν την αλλαγή αλλά τίποτα...). Μάλιστα παρουσιάζω και την απόδειξη ενός τύπου η οποία είναι σε όλη την έκτασή της κατανοητή από κάποιον που γνωρίζει στοιχειώδη θεωρία αριθμών (πλην ενός δύσκολου λήμματος που η απόδειξή του θέλει ισχυρότατα εργαλεία αναλυτικής θεωρίας αριθμών).
(υπάρχουν πολλοί κλειστοί ΚΑΙ αναδρομικοί τύποι σε αντίθεση με αυτό που γράφει το σχολικό βιβλίο στην Α Λυκείου στο εισαγωγικό κεφάλαιο των ακολουθιών ότι τέτοιοι τύποι δεν υπάρχουν. Είχα στείλει έγγραφο στο Υπουργείο πριν χρόνια - όταν ακόμη το κεφάλαιο των προόδων ήταν στη Β Λυκείου - για να κάνουν την αλλαγή αλλά τίποτα...). Μάλιστα παρουσιάζω και την απόδειξη ενός τύπου η οποία είναι σε όλη την έκτασή της κατανοητή από κάποιον που γνωρίζει στοιχειώδη θεωρία αριθμών (πλην ενός δύσκολου λήμματος που η απόδειξή του θέλει ισχυρότατα εργαλεία αναλυτικής θεωρίας αριθμών).Αν είχαμε αποδείξει το παρακάτω ισχυρότερο αποτέλεσμα τότε ίσως να είχαμε απάντηση.Tolaso J Kos έγραψε:Τη παρακάτω άσκηση τη πέτυχα σε βιβλίο. Δεν έχω λύση.
Να εξεταστεί αν υπάρχει σταθεράτέτοια ώστε η τιμή της
να 'ναι πρώτος για κάθε
.
 ,για κάποιον θετικό
,για κάποιον θετικό  .
.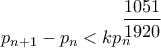 και η πηγή είναι αυτή:
και η πηγή είναι αυτή:Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες