 εκτός κύκλου
εκτός κύκλου  φέρουμε τέμνουσα
φέρουμε τέμνουσα  και εφαπτόμενο τμήμα
και εφαπτόμενο τμήμα 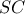 .
.Φέρουμε επίσης
 . Δείξτε ότι :
. Δείξτε ότι : 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 εκτός κύκλου
εκτός κύκλου  φέρουμε τέμνουσα
φέρουμε τέμνουσα  και εφαπτόμενο τμήμα
και εφαπτόμενο τμήμα 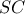 .
. . Δείξτε ότι :
. Δείξτε ότι : 
ΈστωKARKAR έγραψε:Νεότατος γεωμετρικός μέσος.pngΑπό σημείοεκτός κύκλου
φέρουμε τέμνουσα
και εφαπτόμενο τμήμα
.Φέρουμε επίσης
. Δείξτε ότι :
 και
και  .
.  Από το ορθογώνιο τρίγωνο
Από το ορθογώνιο τρίγωνο  ομοκυκλικά οπότε
ομοκυκλικά οπότε  .
. είναι η πολική του σημείου
είναι η πολική του σημείου  ως προς τον κύκλο
ως προς τον κύκλο  προκύπτει ότι η σειρά
προκύπτει ότι η σειρά  είναι αρμονική άρα και η δέσμη
είναι αρμονική άρα και η δέσμη  είναι αρμονική
είναι αρμονική  διχοτόμος της γωνίας
διχοτόμος της γωνίας  και
και  .
. Εξάλλου
Εξάλλου 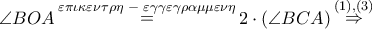
 .
.



 , στο αμέσως προηγούμενο σχήμα του Στάθη και
, στο αμέσως προηγούμενο σχήμα του Στάθη και 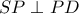 , προκύπτει ότι η
, προκύπτει ότι η  διχοτομεί την γωνία
διχοτομεί την γωνία  και άρα, ισχύει
και άρα, ισχύει  όπου
όπου  .
.
 γιατί η ευθεία
γιατί η ευθεία  περνάει από το κέντρο του κύκλου
περνάει από το κέντρο του κύκλου  .
.
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. Έστω
Έστω  , οι περίκυκλοι των τριγώνων
, οι περίκυκλοι των τριγώνων  και σύμφωνα με το παρακάτω Λήμμα , έχουμε ότι οι κύκλοι αυτοί εφάπτονται των
και σύμφωνα με το παρακάτω Λήμμα , έχουμε ότι οι κύκλοι αυτοί εφάπτονται των  αντιστοίχως, στο σημείο
αντιστοίχως, στο σημείο  και άρα, έχουμε
και άρα, έχουμε 
 και
και  προκύπτει
προκύπτει 


 όπου
όπου  και άρα, τα σημεία
και άρα, τα σημεία  είναι συμμετρικά ως προς την ευθεία
είναι συμμετρικά ως προς την ευθεία  και επομένως ισχύει
και επομένως ισχύει  Συμπεραίνεται έτσι,
Συμπεραίνεται έτσι, 
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. , εκτός δοσμένου κύκλου
, εκτός δοσμένου κύκλου  , φέρνουμε τυχούσα διατέμνουσα
, φέρνουμε τυχούσα διατέμνουσα  και την εφαπτομένη
και την εφαπτομένη 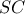 εκατέρωθεν της ευθείας
εκατέρωθεν της ευθείας  , όπου
, όπου  είναι το κέντρο του κύκλου
είναι το κέντρο του κύκλου  και ας είναι
και ας είναι  , η προβολή του σημείου
, η προβολή του σημείου  επί της ευθείας
επί της ευθείας  . Αποδείξτε ότι οι περίκυκλοι έστω
. Αποδείξτε ότι οι περίκυκλοι έστω  , των τριγώνων
, των τριγώνων  , εφάπτονται των
, εφάπτονται των  αντιστοίχως, στο σημείο
αντιστοίχως, στο σημείο  .
. . Πρώτη ύλη της άσκησης αυτό
. Πρώτη ύλη της άσκησης αυτό , εκτός δοσμένου κύκλου
, εκτός δοσμένου κύκλου  , φέρνουμε τυχούσα διατέμνουσα
, φέρνουμε τυχούσα διατέμνουσα  και την εφαπτομένη
και την εφαπτομένη 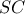 εκατέρωθεν της ευθείας
εκατέρωθεν της ευθείας  , όπου
, όπου  είναι το κέντρο του κύκλου
είναι το κέντρο του κύκλου  και ας είναι
και ας είναι  , η προβολή του σημείου
, η προβολή του σημείου  επί της ευθείας
επί της ευθείας  . Αποδείξτε ότι οι περίκυκλοι έστω
. Αποδείξτε ότι οι περίκυκλοι έστω  , των τριγώνων
, των τριγώνων  , εφάπτονται των
, εφάπτονται των  αντιστοίχως, στο σημείο
αντιστοίχως, στο σημείο  .
. Έστω τα σημεία
Έστω τα σημεία  και
και  , ως τα αντιδιαμετρικά σημεία του
, ως τα αντιδιαμετρικά σημεία του  στους κύκλος
στους κύκλος  αντιστοίχως, λόγω
αντιστοίχως, λόγω  και
και  .
. και
και  , όπου
, όπου  είναι τα κέντρα των κύκλων
είναι τα κέντρα των κύκλων  αντιστοίχως, έχουμε
αντιστοίχως, έχουμε  με
με  .
. με
με  έχουμε
έχουμε 
 και
και 

 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο σε κύκλο έστω
είναι εγγράψιμο σε κύκλο έστω  και άρα, ισχύει
και άρα, ισχύει  .
.
 Αλλά, από εγράψιμα
Αλλά, από εγράψιμα  έχουμε
έχουμε  και
και 


 τώρα, έχουμε
τώρα, έχουμε 


 και
και  , λόγω συμμετρίας των
, λόγω συμμετρίας των  ως προς την ευθεία
ως προς την ευθεία  , προκύπτει
, προκύπτει 
 προκύπτει ότι το τετράπλευρο
προκύπτει ότι το τετράπλευρο  είναι εγγράψιμο σε κύκλο έστω
είναι εγγράψιμο σε κύκλο έστω  και λόγω
και λόγω  συμπεραίνεται ότι είναι ισοσκελές τραπέζιο και επομένως ισχύει
συμπεραίνεται ότι είναι ισοσκελές τραπέζιο και επομένως ισχύει 


 λόγω
λόγω 
 Από
Από  συμπεραίνεται ότι ο κύκλος
συμπεραίνεται ότι ο κύκλος  εφάπτεται της
εφάπτεται της  στο σημείο
στο σημείο  .
. εφάπτεται της
εφάπτεται της 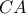 και το Λήμμα έχει αποδειχθεί.
και το Λήμμα έχει αποδειχθεί. είναι όμοια, λόγω
είναι όμοια, λόγω  και άρα ισχύει
και άρα ισχύει 

 και άρα, η ευθεία
και άρα, η ευθεία  διχοτομεί την γωνία
διχοτομεί την γωνία  .
.Καλησπέρα.KARKAR έγραψε:Νεότατος γεωμετρικός μέσος.pngΑπό σημείοεκτός κύκλου
φέρουμε τέμνουσα
και εφαπτόμενο τμήμα
.
Φέρουμε επίσης. Δείξτε ότι :
 και
και 
 ισχύει
ισχύει  κι ακόμη
κι ακόμη 
 εγγράψιμο οπότε
εγγράψιμο οπότε 
 επομένως
επομένως  εφαπτόμενη του περίκυκλου του
εφαπτόμενη του περίκυκλου του 
 οπότε
οπότε  και
και 
 και το ζητούμενο αποδείχτηκε
και το ζητούμενο αποδείχτηκεΜέλη σε αυτήν τη Δ. Συζήτηση: Bing [Bot] και 5 επισκέπτες