Πολυώνυμα - Συλλογή Ασκήσεων
Συντονιστές: achilleas, emouroukos, silouan
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Πολυώνυμα - Συλλογή Ασκήσεων
Μετά την ωραία συλλογή ασκήσεων στο τεύχος 14 του Εικοσιδωδεκαέδρου, ανοίγω καινούργιο θρεντ με νέες.
Τα κριτήριά μου για την επιλογή τους είναι
α) Να μην είναι πολύ απλές (π.χ. εισαγωγικές) στο θέμα αλλά κάπως πιο δύσκολες.
β) Σε καμία περίπτωση να μην είναι δύσκολες, πέραν του "θεμιτού". Απαιτητικές μπορεί να είναι, αλλά η ιδέα είναι να μπορεί να τις λύσει ένας μαθητής που θα αφιερώσει την κατάλληλη σκέψη και εργασία. Στόχος είναι να πάρει εφόδια ο μαθητής και να κάνει προπόνηση στον δρόμο του για προβλήματα σε πιο δύσκολους διαγωνισμούς.
Προαπαιτούμενες γνώσεις: Τα σχολικά αλλά λίγο παραπάνω (π.χ. Vieta κλπ).
Σε λίγο θα βάλω την πρώτη. Υπομονή.
Τα κριτήριά μου για την επιλογή τους είναι
α) Να μην είναι πολύ απλές (π.χ. εισαγωγικές) στο θέμα αλλά κάπως πιο δύσκολες.
β) Σε καμία περίπτωση να μην είναι δύσκολες, πέραν του "θεμιτού". Απαιτητικές μπορεί να είναι, αλλά η ιδέα είναι να μπορεί να τις λύσει ένας μαθητής που θα αφιερώσει την κατάλληλη σκέψη και εργασία. Στόχος είναι να πάρει εφόδια ο μαθητής και να κάνει προπόνηση στον δρόμο του για προβλήματα σε πιο δύσκολους διαγωνισμούς.
Προαπαιτούμενες γνώσεις: Τα σχολικά αλλά λίγο παραπάνω (π.χ. Vieta κλπ).
Σε λίγο θα βάλω την πρώτη. Υπομονή.
Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
ΑΣΚΗΣΗ 1
Έστω ότι η έχει ρίζες
έχει ρίζες  .
.
Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις .
.
Με χρήση των αποτελέσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η εξίσωση να έχει δύο ρίζες ίσες (δηλαδή μία διπλή) είναι
να έχει δύο ρίζες ίσες (δηλαδή μία διπλή) είναι  .
.
Σχόλιο: Το αποτέλεσμα αυτό είναι γνωστότατο και βρίσκεται σε όλα τα βιβλία με τίτλο Theory of Equations, και τα παρεμφερή. Την τοποθετώ εδώ γιατί οι μαθητές μας μπορεί να μην έχουν πρόσβαση στην βιβλιογραφία και γιατί οδηγώ σε διαφορετική απόδειξη από την συνηθισμένη στα βιβλία. Άλλωστε ήθελα να ξεκινήσω με μία κάπως απλή άσκηση. Αργότερα θα βάλω και δυσκολότερες.
Παρακαλώ να αφήσουμε τουλάχιστον την σημερινή ημέρα, Κυριακή 27/11/16, σε προσπάθειες των μαθητών μας.
Έστω ότι η
 έχει ρίζες
έχει ρίζες  .
. Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις
 .
.Με χρήση των αποτελέσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η εξίσωση
 να έχει δύο ρίζες ίσες (δηλαδή μία διπλή) είναι
να έχει δύο ρίζες ίσες (δηλαδή μία διπλή) είναι  .
.Σχόλιο: Το αποτέλεσμα αυτό είναι γνωστότατο και βρίσκεται σε όλα τα βιβλία με τίτλο Theory of Equations, και τα παρεμφερή. Την τοποθετώ εδώ γιατί οι μαθητές μας μπορεί να μην έχουν πρόσβαση στην βιβλιογραφία και γιατί οδηγώ σε διαφορετική απόδειξη από την συνηθισμένη στα βιβλία. Άλλωστε ήθελα να ξεκινήσω με μία κάπως απλή άσκηση. Αργότερα θα βάλω και δυσκολότερες.
Παρακαλώ να αφήσουμε τουλάχιστον την σημερινή ημέρα, Κυριακή 27/11/16, σε προσπάθειες των μαθητών μας.
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Μπορεί να είναι αυτονόητο, αλλά οι ρίζεςMihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 1
Έστω ότι ηέχει ρίζες
.
Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις.
Με χρήση των αποτελέσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η εξίσωσηνα έχει δύο ρίζες ίσες (δηλαδή μία διπλή) είναι
.
Σχόλιο: Το αποτέλεσμα αυτό είναι γνωστότατο και βρίσκεται σε όλα τα βιβλία με τίτλο Theory of Equations, και τα παρεμφερή. Την τοποθετώ εδώ γιατί οι μαθητές μας μπορεί να μην έχουν πρόσβαση στην βιβλιογραφία και γιατί οδηγώ σε διαφορετική απόδειξη από την συνηθισμένη στα βιβλία. Άλλωστε ήθελα να ξεκινήσω με μία κάπως απλή άσκηση. Αργότερα θα βάλω και δυσκολότερες.
Παρακαλώ να αφήσουμε τουλάχιστον την σημερινή ημέρα, Κυριακή 27/11/16, σε προσπάθειες των μαθητών μας.
 είναι όλες πραγματικές ή έχουμε και φανταστικούς αριθμούς;
είναι όλες πραγματικές ή έχουμε και φανταστικούς αριθμούς;Bye :')
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Θα μπορούσαν να είναι και φανταστικές αλλά δέχομαι λύση μόνο για πραγματικούς.JimNt. έγραψε: Μπορεί να είναι αυτονόητο, αλλά οι ρίζεςείναι όλες πραγματικές ή έχουμε και φανταστικούς αριθμούς;
Ας προσθέσω ότι οι τύποι Vieta ισχύουν και για μιγαδικές ρίζες (χωρίς αλλαγή στην απόδειξη) οπότε μπορείς άφοβα να ασχοληθείς με όποια περίπτωση νοιώθεις μεγαλύτερη οικειότητα.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Νομίζω ότι μπορούμε τώρα να ανοίξουμε την άσκηση και για τα μεγάλα παιδιά.
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Καλησπέρα στους φίλουςMihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 1
Έστω ότι ηέχει ρίζες
.
Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις.
Με χρήση των αποτελέσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η εξίσωσηνα έχει δύο ρίζες ίσες (δηλαδή μία διπλή) είναι
.
Σχόλιο: Το αποτέλεσμα αυτό είναι γνωστότατο και βρίσκεται σε όλα τα βιβλία με τίτλο Theory of Equations, και τα παρεμφερή. Την τοποθετώ εδώ γιατί οι μαθητές μας μπορεί να μην έχουν πρόσβαση στην βιβλιογραφία και γιατί οδηγώ σε διαφορετική απόδειξη από την συνηθισμένη στα βιβλία. Άλλωστε ήθελα να ξεκινήσω με μία κάπως απλή άσκηση. Αργότερα θα βάλω και δυσκολότερες.
Παρακαλώ να αφήσουμε τουλάχιστον την σημερινή ημέρα, Κυριακή 27/11/16, σε προσπάθειες των μαθητών μας.
Για ευκολία ονομάζουμε τις συμμετρικές παραστάσεις των
 ως εξής:
ως εξής:


Από τους τύπους Vieta παίρνουμε ότι

Επίσης λόγω της ταυτότητας
 παραγωγίζοντας παίρνουμε
παραγωγίζοντας παίρνουμε
Θέτοντας:



και βάζοντας στην
 διαδοχικά όπου
διαδοχικά όπου  τα
τα  , παίρνουμε την
, παίρνουμε την  και κυκλικά τις υπόλοιπες.
και κυκλικά τις υπόλοιπες.Αν
 οι αντίστοιχες με τις πάνω συμμετρικές παραστάσεις των
οι αντίστοιχες με τις πάνω συμμετρικές παραστάσεις των  τότε αυτές θα είναι ρίζες της εξίσωσης
τότε αυτές θα είναι ρίζες της εξίσωσης  . Συνεπώς αναζητούμε τα
. Συνεπώς αναζητούμε τα  ως συνάρτηση των
ως συνάρτηση των  .
.Κάνοντας (πολύ απλές) πράξεις (με το χέρι) παίρνουμε:

![\begin{aligned}S_2' &= a^2b^2+b^2c^2+c^2a^2 = (ab+bc+ca)^2-2abc(a+b+c)\stackrel{a+b+c=0}{=}(ab+bc+ca)^2 \\ &= \left[3(r_1^2+r_2^2+r_3^2)+3p\right]^2=\left[3(S_1^2-2S_2)+3p\right]^2=9p^2 \ \ (2)\end{aligned} \begin{aligned}S_2' &= a^2b^2+b^2c^2+c^2a^2 = (ab+bc+ca)^2-2abc(a+b+c)\stackrel{a+b+c=0}{=}(ab+bc+ca)^2 \\ &= \left[3(r_1^2+r_2^2+r_3^2)+3p\right]^2=\left[3(S_1^2-2S_2)+3p\right]^2=9p^2 \ \ (2)\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/56fe98d5697d527f9ed5fa7258cc95e1.png)
![\begin{aligned}S_3' &= a^2b^2c^2=(ab)(bc)(ca)=-(3r_1^2+p)(3r_2^2+p)(3r_3^2+p) \\ &= -\left[27r_1^2r_2^2r_3^2+9p(r_1^2r_2^2+r_2^2r_3^2+r_3^2r_1^2)+3p^2(r_1^2+r_2^2+r_3^2)+p^3\right] \\ &= -\left[27S_3^2+9p(S_2^2-2S_1S_3)+3p^2(S_1^2-2S_2)+p^3\right)]=-\left(4p^3+27q^2\right)\end{aligned} \begin{aligned}S_3' &= a^2b^2c^2=(ab)(bc)(ca)=-(3r_1^2+p)(3r_2^2+p)(3r_3^2+p) \\ &= -\left[27r_1^2r_2^2r_3^2+9p(r_1^2r_2^2+r_2^2r_3^2+r_3^2r_1^2)+3p^2(r_1^2+r_2^2+r_3^2)+p^3\right] \\ &= -\left[27S_3^2+9p(S_2^2-2S_1S_3)+3p^2(S_1^2-2S_2)+p^3\right)]=-\left(4p^3+27q^2\right)\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/1c41774df4998c3891bb4d8dc6852aa9.png)
Άρα τελικά οι
 είναι ρίζες της εξίσωσης
είναι ρίζες της εξίσωσης 
Επιπλέον δύο εκ των
 είναι ίσες αν και μόνο αν ισχύει
είναι ίσες αν και μόνο αν ισχύει  δηλαδή αν και μόνο αν
δηλαδή αν και μόνο αν  δηλαδή αν και μόνο αν
δηλαδή αν και μόνο αν  που δίνει την τελική συνθήκη
που δίνει την τελική συνθήκη  .
.Ελπίζω να μην έκανα κάποιο λάθος στις πράξεις.
Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
ΑΣΚΗΣΗ 2
Έστω ότι η έχει μη μηδενικές ρίζες
έχει μη μηδενικές ρίζες  .
.
Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις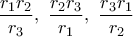 .
.
Με χρήση των αποτελεσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η αρχική εξίσωση να έχει μία ρίζα ίση με το γινόμενο των άλλων δύο είναι
 .
.
Σχόλιο: Η παραπάνω άσκηση μαζί και η προηγούμενη μας δίνει μία τεχνική να βρίσκουμε ικανές και αναγκαίες συνθήκες ώστε τα ισχύει κάποια ταυτότητα μεταξύ των ριζών. Ανάλογα με την περίπτωση, κατασκευάζουμε μία εξίσωση με κατάλληλες ρίζες.
Έστω ότι η
 έχει μη μηδενικές ρίζες
έχει μη μηδενικές ρίζες  .
. Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις
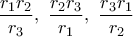 .
.Με χρήση των αποτελεσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η αρχική εξίσωση να έχει μία ρίζα ίση με το γινόμενο των άλλων δύο είναι
 .
.Σχόλιο: Η παραπάνω άσκηση μαζί και η προηγούμενη μας δίνει μία τεχνική να βρίσκουμε ικανές και αναγκαίες συνθήκες ώστε τα ισχύει κάποια ταυτότητα μεταξύ των ριζών. Ανάλογα με την περίπτωση, κατασκευάζουμε μία εξίσωση με κατάλληλες ρίζες.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Δίνω μία διαφορετική λύση της Άσκησης 1, η οποία συγχρόνως υπονοεί μία ωραία τεχνική για τέτοιες ασκήσεις.Mihalis_Lambrou έγραψε:ΑΣΚΗΣΗ 1
Έστω ότι ηέχει ρίζες
.
Βρείτε την τριτοβάθμια εξίσωση που έχει ρίζες τις.
Με χρήση των αποτελέσμάτων σας δείξτε ότι η ικανή και αναγκαία συνθήκη η εξίσωσηνα έχει δύο ρίζες ίσες (δηλαδή μία διπλή) είναι
.
Θέτουμε
 . Θα το εκφράσουμε πρώτα συναρτήσει του
. Θα το εκφράσουμε πρώτα συναρτήσει του 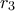 κάνοντας χρήση των
κάνοντας χρήση των  και φυσικά της
και φυσικά της  . Είναι
. Είναι  οπότε
οπότε 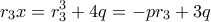 και άρα
και άρα 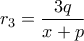
Θέτοντας αυτήν στην
 έπεται
έπεται 
Απλοποιώντας παίρνουμε

Αν αρχίζαμε με άλλη ρίζα στην θέση της
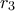 θα καταλήγαμε, εννοείται, στην ίδια. Ας προσεχθεί ότι διαίρεσα με το
θα καταλήγαμε, εννοείται, στην ίδια. Ας προσεχθεί ότι διαίρεσα με το  το οποίο είναι μη μηδενικό επειδή τα
το οποίο είναι μη μηδενικό επειδή τα  είναι μη μηδενικά.
είναι μη μηδενικά.Για το δεύτερο μέρος, η υπόθεση λέει ότι η εξίσωση που βρήκαμε έχει ρίζα την
 , οπότε αμέσως
, οπότε αμέσως 
Φιλικά,
Μιχάλης
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Άσκηση 3
Έστω ακέραιοι.
ακέραιοι.
Θέτουμε
και
1)Για να δειχθεί ότι το
να δειχθεί ότι το  είναι ανάγωγο στο
είναι ανάγωγο στο ![\mathbb{Z}[x] \mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/3488c589add2af2c7b28970f948e3f96.png)
2))Για να δειχθεί ότι το
να δειχθεί ότι το  είναι ανάγωγο στο
είναι ανάγωγο στο ![\mathbb{Z}[x] \mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/3488c589add2af2c7b28970f948e3f96.png)
Υπενθυμίζω.
Το πολυώνυμο με ακέραιους συντελεστές είναι ανάγωγο στο
με ακέραιους συντελεστές είναι ανάγωγο στο ![\mathbb{Z}[x] \mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/3488c589add2af2c7b28970f948e3f96.png)
όταν δεν μπορεί να γραφεί στην μορφή με
με 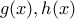 πολυώνυμα με ακέραιους συντελεστές
πολυώνυμα με ακέραιους συντελεστές
που ο βαθμός τους είναι τουλάχιστον
Έστω
 ακέραιοι.
ακέραιοι.Θέτουμε

και

1)Για
 να δειχθεί ότι το
να δειχθεί ότι το  είναι ανάγωγο στο
είναι ανάγωγο στο ![\mathbb{Z}[x] \mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/3488c589add2af2c7b28970f948e3f96.png)
2))Για
 να δειχθεί ότι το
να δειχθεί ότι το  είναι ανάγωγο στο
είναι ανάγωγο στο ![\mathbb{Z}[x] \mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/3488c589add2af2c7b28970f948e3f96.png)
Υπενθυμίζω.
Το πολυώνυμο
 με ακέραιους συντελεστές είναι ανάγωγο στο
με ακέραιους συντελεστές είναι ανάγωγο στο ![\mathbb{Z}[x] \mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/3488c589add2af2c7b28970f948e3f96.png)
όταν δεν μπορεί να γραφεί στην μορφή
 με
με 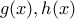 πολυώνυμα με ακέραιους συντελεστές
πολυώνυμα με ακέραιους συντελεστέςπου ο βαθμός τους είναι τουλάχιστον

-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Ενδιαφέρον. Όμως μάλλον πολύ δύσκολο θέμα (ιδίως το δεύτερο ερώτημα) γι αυτό το θρεντ, που το προόριζα για πιο απλές ασκήσεις από ότι οι Ολυμπιάδες. Για εδώ θέλουμε ασκήσεις που ναι με θέλουν κάποια δουλειά, αλλά όχι βαριά τεχνάσματα.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Άσκηση 3
Έστωακέραιοι.
Θέτουμε
και
1)Γιανα δειχθεί ότι το
είναι ανάγωγο στο
2))Γιανα δειχθεί ότι το
είναι ανάγωγο στο
α) Έστω ότι υπάρχουν πολυώνυμα
 με ακέραιους συντελεστές με
με ακέραιους συντελεστές με 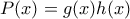 και το καθένα βαθμού μικρότερου του
και το καθένα βαθμού μικρότερου του  . Χωρίς βλάβη ο πρώτος τους συντελεστής είναι
. Χωρίς βλάβη ο πρώτος τους συντελεστής είναι  . Τότε για
. Τότε για 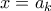 έχουμε
έχουμε
που σημαίνει ότι τα
 είναι το ένα
είναι το ένα  και το άλλο
και το άλλο  .
.Άρα το (μη μηδενικό) πολυώνυμο
 μηδενίζεται σε
μηδενίζεται σε  τιμές, τις
τιμές, τις  , αν και έχει βαθμό μικρότερο του
, αν και έχει βαθμό μικρότερο του  . Άτοπο.
. Άτοπο.β) Πρώτα από όλα το
 είναι απαραίτητο καθώς, π.χ.
είναι απαραίτητο καθώς, π.χ. 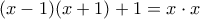 και
και  .
.Για
 έστω
έστω 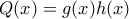 , όπου
, όπου  ως άνω. Έπεται
ως άνω. Έπεται 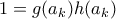
οπότε τα
 είναι είτε και τα δύο
είναι είτε και τα δύο  είτε και τα δύο
είτε και τα δύο  .
. Άρα το
 μηδενίζεται σε
μηδενίζεται σε  τιμές, τις
τιμές, τις  . Αυτό σημαίνει ότι
. Αυτό σημαίνει ότι  και άρα το
και άρα το  έχει άρτιο βαθμό
έχει άρτιο βαθμό  . (Ειδικά δείξαμε το ζητούμενα αν αρχικά είχε περιττό βαθμό.)
. (Ειδικά δείξαμε το ζητούμενα αν αρχικά είχε περιττό βαθμό.)Είναι δηλαδή
 .
. Άρα

Ειδικά οι ρίζες των
 είναι
είναι  (τις μισές το ένα, τις άλλες μισές το άλλο). Oπότε κάποια αναδιάταξη
(τις μισές το ένα, τις άλλες μισές το άλλο). Oπότε κάποια αναδιάταξη  των
των  είναι
είναι 
Αλλά τότε για τις
 τιμές
τιμές  έχουμε
έχουμε  , οπότε
, οπότε  και όμοια γιά τα
και όμοια γιά τα  . 'Ετσι γράφουμε το
. 'Ετσι γράφουμε το  με πολλούς τρόπους ως γινόμενο δύο παραγόντων, ενώ ξέρουμε ότι υπάρχουν μόνο τέσσερις:
με πολλούς τρόπους ως γινόμενο δύο παραγόντων, ενώ ξέρουμε ότι υπάρχουν μόνο τέσσερις:  . Άτοπο.
. Άτοπο.-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Μιχάλη τις θεώρησα απλές για αυτό τις έβαλα.
Αυτές και κάποιες άλλες (δύσκολες) τις ξέρω από τότε που ήμουν μαθητής Λυκείου.
Για την 2) υπάρχει και διαφορετικό τελείωμα.
Εχουμε
Αν θέσουμε τότε το αριστερό μέλος είναι αρνητικό και κατά απόλυτη τιμή μεγαλύτερο
τότε το αριστερό μέλος είναι αρνητικό και κατά απόλυτη τιμή μεγαλύτερο
από
που μας δίνει το ΑΤΟΠΟ.
Αυτές και κάποιες άλλες (δύσκολες) τις ξέρω από τότε που ήμουν μαθητής Λυκείου.
Για την 2) υπάρχει και διαφορετικό τελείωμα.
Εχουμε

Αν θέσουμε
 τότε το αριστερό μέλος είναι αρνητικό και κατά απόλυτη τιμή μεγαλύτερο
τότε το αριστερό μέλος είναι αρνητικό και κατά απόλυτη τιμή μεγαλύτερο από

που μας δίνει το ΑΤΟΠΟ.
-
stranton
- Επιμελητής
- Δημοσιεύσεις: 679
- Εγγραφή: Πέμ Ιουν 25, 2009 5:00 pm
- Τοποθεσία: Σπάρτη
- Επικοινωνία:
Re: Πολυώνυμα - Συλλογή Ασκήσεων
ΑΣΚΗΣΗ 4
Θεωρούμε το πολυώνυμο με ακέραιους συντελεστές,
με ακέραιους συντελεστές,
για το οποίο δίνεται ότι .
.
Να αποδείξετε ότι δεν υπάρχει ακέραιος ώστε
ώστε  .
.
Θεωρούμε το πολυώνυμο
 με ακέραιους συντελεστές,
με ακέραιους συντελεστές, για το οποίο δίνεται ότι
 .
. Να αποδείξετε ότι δεν υπάρχει ακέραιος
 ώστε
ώστε  .
.Στράτης Αντωνέας
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Μας αρκούν πολύ λιγότερες υποθέσεις. Π.χ. μόνο μεstranton έγραψε:ΑΣΚΗΣΗ 4
Θεωρούμε το πολυώνυμομε ακέραιους συντελεστές,
για το οποίο δίνεται ότι.
Να αποδείξετε ότι δεν υπάρχει ακέραιοςώστε
.

ή μόνο
 για κάποιους διαφορετικούς ανά δύο ακέραιους. Ας δούμε το πρώτο, παρόμοια το δεύτερο.
για κάποιους διαφορετικούς ανά δύο ακέραιους. Ας δούμε το πρώτο, παρόμοια το δεύτερο.Από υπόθεση το
 έχει τα
έχει τα  ως ρίζες, άρα υπάρχει πολυώνυμο
ως ρίζες, άρα υπάρχει πολυώνυμο  με ακέραιους συντελεστές τέτοιο ώστε
με ακέραιους συντελεστές τέτοιο ώστε  .
. Αν
 για κάποιον ακέραιο
για κάποιον ακέραιο  τότε
τότε  . Άτοπο γιατί ο
. Άτοπο γιατί ο  δεν έχει διαιρέτες που διαφέρουν κατά
δεν έχει διαιρέτες που διαφέρουν κατά  όπως είναι οι
όπως είναι οι  .
.-
panagiotis99
- Δημοσιεύσεις: 133
- Εγγραφή: Δευ Φεβ 04, 2013 8:24 pm
- Τοποθεσία: Αθηνα
Re: Πολυώνυμα - Συλλογή Ασκήσεων
ΑΣΚΗΣΗ 5
Καλησπέρα, προτείνω το παρακάτω:
Να βρεθούν όλα τα μη-σταθερά πραγματικά πολυώνυμα ώστε για κάθε
ώστε για κάθε  ισχύει:
ισχύει:

Καλησπέρα, προτείνω το παρακάτω:
Να βρεθούν όλα τα μη-σταθερά πραγματικά πολυώνυμα
 ώστε για κάθε
ώστε για κάθε  ισχύει:
ισχύει:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Μία λύση είναι η προφανής,panagiotis99 έγραψε:ΑΣΚΗΣΗ 5
Να βρεθούν όλα τα μη-σταθερά πραγματικά πολυώνυμαώστε για κάθε
ισχύει:
 . Θα δούμε ότι δεν υπάρχουν άλλες.
. Θα δούμε ότι δεν υπάρχουν άλλες.Γράφουμε
 .
. Θέτωντας
 στην δοθείσα έπεται
στην δοθείσα έπεται  , άρα
, άρα  οπότε
οπότε  , δηλαδή
, δηλαδή  (το άθροισμα αρχίζει από το
(το άθροισμα αρχίζει από το  )
)Από την δοθείσα έχουμε για κάθε
 ότι
ότι ![\displaystyle{ \sum _{k=1}^n a_k \left [(\sin x+\cos x)^k - \sin ^k x - \cos ^k x \right ]=0} \displaystyle{ \sum _{k=1}^n a_k \left [(\sin x+\cos x)^k - \sin ^k x - \cos ^k x \right ]=0}](/forum/ext/geomar/texintegr/latexrender/pictures/ffcb6a3ea6bed37be60b79a7d5b244db.png)
Παρατηρούμε ότι ο όρος για
 μέσα στην αγκύλη μηδενίζεται, οπότε η προηγούμενη γράφεται τελικά
μέσα στην αγκύλη μηδενίζεται, οπότε η προηγούμενη γράφεται τελικά ![\displaystyle{ \sum _{k=2}^n a_k \left [(\sin x+\cos x)^k - \sin ^k x - \cos ^k x \right ]=0} \, (*) \displaystyle{ \sum _{k=2}^n a_k \left [(\sin x+\cos x)^k - \sin ^k x - \cos ^k x \right ]=0} \, (*)](/forum/ext/geomar/texintegr/latexrender/pictures/8028242ec20751ff4277bb3e064727b6.png) (το άθροισμα αρχίζει από το
(το άθροισμα αρχίζει από το  )
)Θέτουμε τώρα
 .
.Για τυπογραφική ευκολία θα συμβολίζω τα
 ως
ως  αντίστοιχα. Ειδικά
αντίστοιχα. Ειδικά  . Εύκολα βλέπουμε επαγωγικά ότι για
. Εύκολα βλέπουμε επαγωγικά ότι για 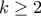 οι παραστάσεις
οι παραστάσεις  είναι πολυώνυμα βαθμού
είναι πολυώνυμα βαθμού  ως προς
ως προς  . Η αρχή γίνεται από το
. Η αρχή γίνεται από το
ενώ για τον γενικό όρο
 μπορούμε να χρησιμοποιήσουμε το ανάπτυγμα του διωνύμου και να ζευγαρώσουμε συμμετρικούς όρους
μπορούμε να χρησιμοποιήσουμε το ανάπτυγμα του διωνύμου και να ζευγαρώσουμε συμμετρικούς όρους  . Αφού το κάνουμε, τον κοινό παράγοντα
. Αφού το κάνουμε, τον κοινό παράγοντα  τον γράφουμε
τον γράφουμε  , και λοιπά.
, και λοιπά. Τελικά, ως προς τα πολυώνυμα
 η
η  γράφεται
γράφεται 
Επειδή η ισότητα αυτή ισχύει για άπειρα
 , συμπεραίνουμε ότι
, συμπεραίνουμε ότι  , και άρα το ζητούμενο πολυώνυμο είναι πρώτου βαθμού (χωρίς σταθερό όρο).
, και άρα το ζητούμενο πολυώνυμο είναι πρώτου βαθμού (χωρίς σταθερό όρο).Σχόλιο: Η άσκηση μάλλον ξεφεύγει από τους στόχους που είχα κατά νου γι' αυτό το θρεντ ως δύσκολη, εκτός αν δεν βλέπω κάτι.
-
stranton
- Επιμελητής
- Δημοσιεύσεις: 679
- Εγγραφή: Πέμ Ιουν 25, 2009 5:00 pm
- Τοποθεσία: Σπάρτη
- Επικοινωνία:
Re: Πολυώνυμα - Συλλογή Ασκήσεων
ΑΣΚΗΣΗ 6
Έστω πολυώνυμο βαθμού
πολυώνυμο βαθμού  , για το οποίο δίνεται ότι
, για το οποίο δίνεται ότι  για
για  .
.
Να βρείτε το .
.
Έστω
 πολυώνυμο βαθμού
πολυώνυμο βαθμού  , για το οποίο δίνεται ότι
, για το οποίο δίνεται ότι  για
για  .
. Να βρείτε το
 .
.Στράτης Αντωνέας
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Ακόμα καλύτερα μπορούμε να βρούμε το ίδιο το πολυώνυμο:stranton έγραψε:ΑΣΚΗΣΗ 6
Έστωπολυώνυμο βαθμού
, για το οποίο δίνεται ότι
για
.
Να βρείτε το.
Από την υπόθεση έπεται ότι το πολυώνυμο
 βαθμού
βαθμού  έχει τις
έχει τις  ρίζες , τις
ρίζες , τις  . Άρα
. Άρα 
Θέτωντας
 βρίσκουμε
βρίσκουμε  . Άρα
. Άρα 
Ας παρατηρήσουμε ότι ο σταθερός όρος της παράστασης μέσα στην μεγάλη παρένθεση είναι μηδέν, οπότε μετά την απλοποίηση του παρονομαστή
 , βλέπουμε πολυώνυμο στο δεξί μέλος.
, βλέπουμε πολυώνυμο στο δεξί μέλος.Τέλος
 .
.-
VASILIS_VLH
- Δημοσιεύσεις: 7
- Εγγραφή: Τετ Νοέμ 30, 2011 10:19 pm
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Αν το πολυώνυμο  δεν έχει ρίζες και ισχύει ότι
δεν έχει ρίζες και ισχύει ότι  , να βρεθεί το πρόσημο του
, να βρεθεί το πρόσημο του  .
.
 δεν έχει ρίζες και ισχύει ότι
δεν έχει ρίζες και ισχύει ότι  , να βρεθεί το πρόσημο του
, να βρεθεί το πρόσημο του  .
.Βλαχοβασίλης Βασίλειος
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Πολυώνυμα - Συλλογή Ασκήσεων
ΑρχικάVASILIS_VLH έγραψε:Αν το πολυώνυμοδεν έχει ρίζες και ισχύει ότι
, να βρεθεί το πρόσημο του
.
 διότι διαφορετικά το
διότι διαφορετικά το  θα ήταν ρίζα του πολυωνύμου.
θα ήταν ρίζα του πολυωνύμου.Η δοσμένη σχέση
 είναι ισοδύναμη της
είναι ισοδύναμη της  .
. Αν ήταν
 δηλαδή
δηλαδή  , τότε λόγω συνέχειας της
, τότε λόγω συνέχειας της  , ισχύουν οι προϋποθέσεις του θεωρήματος Bolzano στο
, ισχύουν οι προϋποθέσεις του θεωρήματος Bolzano στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) δηλαδή η εξίσωση
δηλαδή η εξίσωση  έχει τουλάχιστον μία ρίζα στο
έχει τουλάχιστον μία ρίζα στο  , άτοπο.
, άτοπο.Άρα
 .
.Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Πολυώνυμα - Συλλογή Ασκήσεων
Επαναφέρω την ΑΣΚΗΣΗ 2.
Επίσης
Επίσης
Ας την ονομάσουμε ΑΣΚΗΣΗ 7, για να έχουν ρέουσα αρίθμηση.VASILIS_VLH έγραψε:Αν το πολυώνυμοδεν έχει ρίζες και ισχύει ότι
, να βρεθεί το πρόσημο του
.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 0 επισκέπτες
