Ας το δούμε και με μιγαδική ανάλυση:
Έστω πολυώνυμο

ώστε

για κάθε

με

. Έστω

οι ρίζες του

μέσα στον μοναδιαίο δίσκο και

οι ρίζες του

έξω από τον μοναδιαίο δίσκο. (Με πολλαπλότητα.)
Τότε
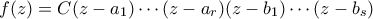
για κάποιο

. Θεωρώ το πολυώνυμο

.
Παρατηρώ ότι το

δεν έχει ρίζα μέσα στον μοναδιαίο δίσκο. Επίσης

για κάθε

με

.
Από το maximum modulus principle, είναι

Από το minimum modulus principle (αφού η

δεν μηδενίζεται στον μοναδιαίο δίσκο) είναι

Άρα για κάθε

με

έχουμε

. Επομένως μέσα στον μοναδιαίο δίσκο μπορούμε να ορίσουμε την συνάρτηση

. Αυτή η συνάρτηση θα έχει σταθερό πραγματικό μέρος και επομένως (π.χ. από τις εξισώσεις Cauchy-Riemann) θα έχουμε ότι στον μοναδιαίο δίσκο η

είναι σταθερή. Άρα και η

είναι σταθερή στον μοναδιαίο δίσκο.
Από εδώ λαμβάνουμε
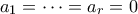
και επιπλέον

. Άρα

όπως θέλαμε να δείξουμε.

Ουσιαστικά η ίδια απόδειξη δείχνει ότι το ίδιο συμπέρασμα ισχύει ακόμη και αν η

είναι οποιαδήποτε μιγαδικώς παραγωγίσιμη συνάρτηση. Το μόνο επιπλέον στοιχείο που χρειάζεται είναι ότι κάθε τέτοια συνάρτηση έχει πεπερασμένο πλήθος ριζών (μετρώντας και την πολλαπλότητα) μέσα στον μοναδιαίο δίσκο.
 , όπου
, όπου  , ισχύει η
, ισχύει η  για κάθε
για κάθε  τέτοιο ώστε
τέτοιο ώστε  , τότε
, τότε  και
και  .
. ισχύει, με
ισχύει, με  και
και  , η
, η  , καθότι ισχύουν οι
, καθότι ισχύουν οι  και
και  . Ύστερα από τις πράξεις προκύπτει η ισότητα
. Ύστερα από τις πράξεις προκύπτει η ισότητα
 πάντοτε. Θέτοντας
πάντοτε. Θέτοντας  και
και  προκύπτουν οι ισότητες
προκύπτουν οι ισότητες και
και 
 και, λόγω της
και, λόγω της  ,
,  . Αλλά η
. Αλλά η  δίνει
δίνει  , και, λόγω της
, και, λόγω της  και πάλι,
και πάλι, 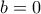 .
. ,
, 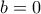 και την αρχική συνθήκη προκύπτει η
και την αρχική συνθήκη προκύπτει η  για
για  , οπότε
, οπότε  .
.
 για κάθε
για κάθε  τότε
τότε  ,
,  για
για  (προβολή Fourier).
(προβολή Fourier). μπορούμε να εκφράσουμε το
μπορούμε να εκφράσουμε το  με αυτόν τον τρόπο και, επειδή
με αυτόν τον τρόπο και, επειδή  , από το λήμμα ο σταθερός όρος του
, από το λήμμα ο σταθερός όρος του  μηδενίζεται. Τα υπόλοιπα είναι επαγωγή.
μηδενίζεται. Τα υπόλοιπα είναι επαγωγή. είναι ένα τριγωνομετρικό πολυώνυμο
είναι ένα τριγωνομετρικό πολυώνυμο )
)![x\in [0,2\pi ]\Rightarrow T(x)=0 x\in [0,2\pi ]\Rightarrow T(x)=0](/forum/ext/geomar/texintegr/latexrender/pictures/78767291cb503d50b66cd6bb89a1aede.png)

 για
για  και
και 
 , οπότε, με δεδομένη την
, οπότε, με δεδομένη την  και
και  .
. ...]
...] ώστε
ώστε  για κάθε
για κάθε  . Έστω
. Έστω  οι ρίζες του
οι ρίζες του  οι ρίζες του
οι ρίζες του 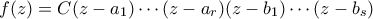 για κάποιο
για κάποιο  . Θεωρώ το πολυώνυμο
. Θεωρώ το πολυώνυμο  .
. δεν έχει ρίζα μέσα στον μοναδιαίο δίσκο. Επίσης
δεν έχει ρίζα μέσα στον μοναδιαίο δίσκο. Επίσης  για κάθε
για κάθε 

 έχουμε
έχουμε  . Αυτή η συνάρτηση θα έχει σταθερό πραγματικό μέρος και επομένως (π.χ. από τις εξισώσεις Cauchy-Riemann) θα έχουμε ότι στον μοναδιαίο δίσκο η
. Αυτή η συνάρτηση θα έχει σταθερό πραγματικό μέρος και επομένως (π.χ. από τις εξισώσεις Cauchy-Riemann) θα έχουμε ότι στον μοναδιαίο δίσκο η  είναι σταθερή. Άρα και η
είναι σταθερή. Άρα και η  είναι σταθερή στον μοναδιαίο δίσκο.
είναι σταθερή στον μοναδιαίο δίσκο.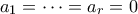 και επιπλέον
και επιπλέον  . Άρα
. Άρα  όπως θέλαμε να δείξουμε.
όπως θέλαμε να δείξουμε.
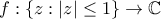


 και
και 



 στο
στο