 με
με 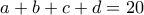 .
.Συντονιστές: Demetres, socrates, silouan
Θα πρέπει όλα τα ψηφία να είναι απόJimNt. έγραψε:Να βρείτε το πλήθος των θετικών ακεραίωνμε
.
 έως
έως  εκτός από το
εκτός από το  που πρέπει να είναι από
που πρέπει να είναι από  έως
έως  .
.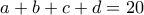 . Ισοδύναμα θα βρούμε το πλήθος των διατάξεων ενός δυαδικού αριθμού με
. Ισοδύναμα θα βρούμε το πλήθος των διατάξεων ενός δυαδικού αριθμού με  άσσους και
άσσους και  μηδενικά (που λειτουργούν ως διαχωριστικά των
μηδενικά (που λειτουργούν ως διαχωριστικά των  ,
,  ,
,  και
και  . Έχουμε δηλαδή:
. Έχουμε δηλαδή: λύσεις.
λύσεις. ,
,  ,
,  και
και  να είναι
να είναι 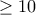 . Θα πάμε με PIE:
. Θα πάμε με PIE: τότε θέτουμε
τότε θέτουμε  με
με 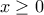 και η εξίσωση γίνεται:
και η εξίσωση γίνεται:
 λύσεις.
λύσεις. και
και  τότε θέτουμε
τότε θέτουμε  και
και  με
με 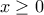 και
και  και η εξίσωση γίνεται:
και η εξίσωση γίνεται:
 λύση.
λύση. από
από  ,
,  ,
,  και
και  να είναι
να είναι 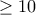 , τότε δεν υπάρχει καμία λύση.
, τότε δεν υπάρχει καμία λύση. ,
,  ,
,  και
και  να είναι
να είναι 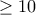 είναι:
είναι:
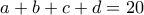 , ώστε τα
, ώστε τα  ,
,  ,
,  και
και  να είναι
να είναι  , είναι:
, είναι: 
 .
.  , ώστε τα
, ώστε τα  ,
,  και
και  να είναι
να είναι  .
. ,
,  και
και  με
με  και η εξίσωση γίνεται:
και η εξίσωση γίνεται:
 ισχύει έτσι και αλλιώς, επομένως αρκεί να βρούμε το πλήθος των μη αρνητικών λύσεων της εξίσωσης. Έχουμε δηλαδή:
ισχύει έτσι και αλλιώς, επομένως αρκεί να βρούμε το πλήθος των μη αρνητικών λύσεων της εξίσωσης. Έχουμε δηλαδή: λύσεις.
λύσεις. λύσεις.
λύσεις. , ώστε τα
, ώστε τα  ,
,  και
και  να είναι
να είναι  .
. ,
,  και
και  με
με  και η εξίσωση γίνεται:
και η εξίσωση γίνεται:
 ισχύει έτσι και αλλιώς, επομένως αρκεί να βρούμε το πλήθος των μη αρνητικών λύσεων της εξίσωσης.
ισχύει έτσι και αλλιώς, επομένως αρκεί να βρούμε το πλήθος των μη αρνητικών λύσεων της εξίσωσης.  είναι λύση χωρίς να πληρεί τον περιορισμό.
είναι λύση χωρίς να πληρεί τον περιορισμό.Κύριε Σταύρο μάλλον δεν ήταν σαφές αυτό που έγραψα!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Δεν είναι σωστό.Διονύσιος Αδαμόπουλος έγραψε: Θα βρούμε το πλήθος των μη αρνητικών λύσεων της εξίσωσης, ώστε τα
,
και
να είναι
.
Θέτουμε,
και
με
και η εξίσωση γίνεται:
Όμως στην εξίσωση που φτάσαμε ο περιορισμόςισχύει έτσι και αλλιώς, επομένως αρκεί να βρούμε το πλήθος των μη αρνητικών λύσεων της εξίσωσης.
π.χείναι λύση χωρίς να πληρεί τον περιορισμό.
Εκανες κύκλο.
 , ώστε τα
, ώστε τα  .
. , ώστε τα
, ώστε τα  .
.Κώδικας: Επιλογή όλων
int main()
{
int x, y, z, p=0;
for (x=0; x<=9; x++)
for (y=0; y<=9; y++)
for (z=0; z<=9; z++)
if (x+y+z==20)
p++;
printf("%d\n",p);
return 0;
}
Κώδικας: Επιλογή όλων
int main()
{
int x, y, z, p=0;
for (x=0; x<=9; x++)
for (y=0; y<=9; y++)
for (z=0; z<=9; z++)
if (x+y+z==7)
p++;
printf("%d\n",p);
return 0;
}
 .
. (αφού κανένα από αυτά δεν πρόκειται να βγει πάνω από
(αφού κανένα από αυτά δεν πρόκειται να βγει πάνω από  ) και μπορεί να λυθεί εύκολα πλέον με το γνωστό λήμμα της συνδυαστικής, δίνοντας
) και μπορεί να λυθεί εύκολα πλέον με το γνωστό λήμμα της συνδυαστικής, δίνοντας  λύσεις, όσες μου δίνουν και τα δύο παραπάνω προγράμματα.
λύσεις, όσες μου δίνουν και τα δύο παραπάνω προγράμματα.Κώδικας: Επιλογή όλων
int main()
{
int a, b, c, d, p=0;
for (a=1; a<=9; a++)
for (b=0; b<=9; b++)
for (c=0; c<=9; c++)
for (d=0; d<=9; d++)
if (a+b+c+d==20)
p++;
printf("%d\n",p);
return 0;
}
 , όσες δηλαδή βρήκα στην αρχική λύση μου.
, όσες δηλαδή βρήκα στην αρχική λύση μου.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες