Μεγιστοποίηση γωνίας

#1

Ένας συνάδελφος φυσικός θέλει να του λύσουμε το εξής πρόβλημα :

Μέσα σε ένα κύκλο με κέντρο Ο έχουμε ένα σημείο Α. Στο κύκλο κινείται ένα σημείο Μ. Θέλουμε να μεγιστοποιήσουμε τη γωνία OMA

.Πώς θα το πεtύχουμε ;

Μπ.

#2

Μπάμπης Στεργίου έγραψε:Ένας συνάδελφος φυσικός θέλει να του λύσουμε το εξής πρόβλημα :

Μέσα σε ένα κύκλο με κέντρο Ο έχουμε ένα σημείο Α. Στο κύκλο κινείται ένα σημείο Μ. Θέλουμε να μεγιστοποιήσουμε τη γωνία .Πώς θα το πεtύχουμε ;

Μπ.

Γεια σου Μπάμπη!

Νομίζω όταν $\displaystyle{OA \bot AM}$ (δεν το έχω αποδείξει).

Al.Koutsouridis · #3

Μπάμπης Στεργίου έγραψε:Ένας συνάδελφος φυσικός θέλει να του λύσουμε το εξής πρόβλημα :

Μέσα σε ένα κύκλο με κέντρο Ο έχουμε ένα σημείο Α. Στο κύκλο κινείται ένα σημείο Μ. Θέλουμε να μεγιστοποιήσουμε τη γωνία .Πώς θα το πεtύχουμε ;

Μπ.

Χωρίς να το έχω κοιτάξει διεξοδικά...

Αντί να κινούμε το σημείο

λόγο της συμμετρίας του κύκλου μπορούμε να θεωρήσουμε το

σταθερό και να κινούμε το

. Τότε το

κινείται σε κύκλο ακτίνας

και η μέγιστη γωνία επιτυγχάνεται όταν

είναι εφαπτομένη σε αυτό τον κύκλο.

Για την κατασκευή, αρκεί να φέρουμε την κάθετη στο

στο

και τα σημεία τομής της με το κύκλο δίνουν τα ζητούμενα

.

#4

: Babis.png (11.05 KiB) Προβλήθηκε 1920 φορές

$\displaystyle{\sin \omega = \frac{{OE}}{R} \le \frac{{OA}}{R} = \sin \theta \Leftrightarrow \omega \le \theta }$ ( $\omega, \theta$ οξείες)

#5

: Μέγιστο γωνίας για συνάδελφο.png (33.84 KiB) Προβλήθηκε 1898 φορές

Για δείτε κι αυτό. Σε λίγο και δυο λόγια .

Ας είναι

το κέντρο του κύκλου (M,O,A)

και

η ακτίνα του . Προφανώς το

ανήκει στη σταθερή μεσοκάθετο

του

. Επειδή $2r \geqslant R$ και $\widehat \theta = \widehat \omega$ η ακτίνα

γίνεται ελάχιστη όταν οι κύκλοι εφάπτονται και $r = \dfrac{R}{2}$ τότε ο λόγος $\dfrac{{NA}}{r}$ γίνεται

μέγιστος και αφού στο διάστημα $[0,\dfrac{\pi }{2}]$ η $y = \sin x$ γνήσια αύξουσα θα έχουμε τη

μέγιστη γωνία $\widehat \theta$ . Προφανώς τότε $MA \bot OA$ .

#6

Η μέθοδος λύσης είναι ακριβώς η ίδια με του προβλήματος Regiomontanus που είδαμε π.χ.

εδώ

Λεπτομερέστερα, γράφουμε τον κύκλο που διέρχεται από τα

και

και ο οποίος εφάπτεται
του κύκλου. Το σημείο επαφής είναι το ζητούμενο. Η απόδειξη είναι ακριβώς ίδια με του αρχικού προβλήματος Regiomontanus όπου το

κινείται σε ευθεία αντί στον κύκλο.

Ας σημειώσω ότι δεν είναι σύμπτωση ότι τα δύο προβλήματα έχουν ακριβώς την ίδια λύση. Πραγματικά, αν κάνουμε αντιστροφή ανάγουμε το ένα πρόβλημα στο άλλο.

#7

Σας ευχαριστώ πολύ !!!

Στο μεταξύ, από τη στιγμή που έβαλα το πρόβλημα και ασχολήθηκα σε ένα κενό μια και έλειπε η γ' Λυκείου, κατέληξα στο ίδιο αποτέλεσμα ως εξής: Βρήκα ψάχνοντας - όπως ο Νίκος - ότι το ζητούμενο σημείο είναι εκεί που εφάπτεται ο κύκλος που περνάει από τα O,A

με τον αρχικό κύκλο, μια και για τα άλλα σημεία του κύκλου η γωνία

είναι εσωτερική ενός τριγώνου και έτσι μικρότερη από την εξωτερική, που ως εγγραμμένη είναι ίση με τον ''οριακή'' γωνία στο σημείο επαφής.
Για την κατασκευή του κύκλου αυτού, αρκεί να φέρουμε χορδή

του μεγάλου κύκλου παράλληλη με την

και με μήκος 2OA

.Το ζητούμενο σημείο

είναι η τομή των BA,CO

, κάτι που εξασφαλίζεται με μια απλή ομοιοθεσία. Σίγουρα έχω κάνει περισσότερα από όσα χρειάζονται, τα αναφέρω όμως μόνο για αρχειακούς λόγους.

Μιχάλη, αν και ήξερα -από το βιβλίο που έχεις επιμεληθεί(νομίζω στα τριγωνομετρικά λυκούμια ή στο άλλο με το e) - για το πρόβλημα του Johannes Mueller με το άγαλμα, δεν ήξερα ότι αυτό με τον κύκλο είναι το ανάλογο , μάλλον το ίδιο ! Και πράγματι είναι !Υπέροχα πράγματα από την ιστορία των μαθηματικών, που είναι γεμάτη συγκινήσεις.

Επεχείρησα και τη μέθοδο του Γιώργου, έφτιαξα το τρίγωνο, κάτι μου φάνηκε πως δεν βγαίνει και κατέληξα στον κύκλο που και αυτό μάλλον δείχνει ένας φυσιολογικός δρόμος(εκ των υστέρων πάντα !)

Χρόνια πολλά σε όλους και Χριστός ανέστη !!!

#8

Καλησπέρα σε όλους. Εφόσον βρισκόμαστε σε φάκελο καθηγητή μπορούμε να πειραματιζόμαστε με διάφορα εργαλεία των Μαθηματικών. Ασφαλώς και υπάρχουν οι ταχύτερες και κομψότερες λύσεις των εκλεκτών φίλων στις προηγούμενες αναρτήσεις.

Η περιέργεια για το αν μπορεί να γίνει διερεύνηση του προβλήματος, ξεκινώντας από Καρτεσιανό σύστημα συντεταγμένων, με οδήγησε σε μια ευχάριστη (υποκειμενική άποψη, εννοείται) περιήγηση. Την μοιράζομαι με όποιον θα ήθελε να διαβεί την ίδια διαδρομή:

: 27-04-2017 Γεωμετρία.png (19.75 KiB) Προβλήθηκε 1801 φορές

Έστω

κύκλος κέντρου O(0,0)

και σημείο A(a, b), 0 < a^2+b^2<1

.

Παίρνουμε σημείο $\displaystyle M\left( {{x_0},\;{y_0}} \right),\;\;x_0^2 + y_0^2 = 1$ , οπότε $\displaystyle \mathop {{\rm M}{\rm O}}\limits^ \to = \left( { - {x_0},\; - {y_0}} \right),\;\;\mathop {{\rm M}A}\limits^ \to = \left( {a - {x_0},b\; - {y_0}} \right)$

Έστω $\displaystyle \varphi = \widehat {{\rm O}{\rm M}{\rm A}}$ , οπότε $\displaystyle \sigma \upsilon \nu \varphi = \frac{{\mathop {{\rm M}{\rm O}}\limits^ \to \cdot \mathop {{\rm M}{\rm A}}\limits^ \to }}{{\left| {\mathop {{\rm M}{\rm O}}\limits^ \to } \right| \cdot \left| {\mathop {{\rm M}{\rm A}}\limits^ \to } \right|}} = \frac{{\left( { - {x_0},\; - {y_0}} \right)\left( {a - {x_0},b\; - {y_0}} \right)}}{{1 \cdot \;\sqrt {{{\left( {a - {x_0}} \right)}^2} + {{\left( {b\; - {y_0}} \right)}^2}} }} =$

$\displaystyle = \frac{{ - a{x_0} + x_0^2 - b{y_0} + y_0^2}}{{\;\sqrt {{a^2} - 2a{x_0} + x_0^2 + {b^2} - 2b{y_0} + y_0^2} }} = \frac{{1 - a{x_0} - b{y_0}}}{{\;\sqrt {{a^2} - 2a{x_0} + 1 + {b^2} - 2b{y_0}} }} =$
$\displaystyle = \frac{{1 - \left( {a{x_0} + b{y_0}} \right)}}{{\sqrt {{a^2} + {b^2} + 1 - 2\left( {a{x_0} + b{y_0}} \right)} }}.$

Είναι $\displaystyle \mathop {OM}\limits^ \to = \left( {{x_0},\;{y_0}} \right),\;\;\mathop {OA}\limits^ \to = \left( {a,\;b} \right)$ άρα

$\displaystyle a{x_0} + \;b{y_0} = \mathop {OM}\limits^ \to \, \cdot \mathop {OA}\limits^ \to = \left| {\mathop {OM}\limits^ \to \,} \right| \cdot \left| {\mathop {OA}\limits^ \to } \right| \cdot \sigma \upsilon \nu \theta = 1 \cdot \sqrt {{a^2} + {b^2}} \cdot \sigma \upsilon \nu \theta = \lambda \sigma \upsilon \nu \theta ,$

όπου $\displaystyle \left| {\mathop {OA}\limits^ \to } \right| = \;\sqrt {{a^2} + {b^2}} = \lambda ,\;\;\widehat {{\rm A}{\rm O}{\rm M}} = \theta ,\;\;0 \le \theta \le \pi$ .

Τότε $\displaystyle \sigma \upsilon \nu \varphi = \frac{{1 - \lambda \sigma \upsilon \nu \theta }}{{\sqrt {{\lambda ^2} + 1 - 2\lambda \sigma \upsilon \nu \theta } }}.$

Η συνάρτηση $\displaystyle f\left( x \right) = \frac{{1 - \lambda \sigma \upsilon \nu x}}{{\sqrt {{\lambda ^2} + 1 - 2\lambda \sigma \upsilon \nu x} }}$ ορίζεται για κάθε $\displaystyle x \in \left[ {0,\;\pi } \right]$ , αφού

$\displaystyle \left| {\sigma \upsilon \nu x} \right| \le 1 \Leftrightarrow \left| {2\lambda \sigma \upsilon \nu x} \right| \le 2\lambda < {\lambda ^2} + 1$ , για κάθε $\displaystyle \lambda \in \left( {0,\;1} \right)$ .

Έχει παράγωγο $\displaystyle f'\left( x \right) = \frac{{\lambda \eta \mu x \cdot \sqrt {{\lambda ^2} + 1 - 2\lambda \sigma \upsilon \nu x} - \left( {1 - \lambda \sigma \upsilon \nu x} \right)\frac{{\lambda \eta \mu x}}{{\sqrt {{\lambda ^2} + 1 - 2\lambda \sigma \upsilon \nu x} }}}}{{\left( {{\lambda ^2} + 1 - 2\lambda \sigma \upsilon \nu x} \right)}} =$

$\displaystyle = \frac{{{\lambda ^2}\eta \mu x \cdot \left( {\lambda - \sigma \upsilon \nu x} \right)}}{{\left( {{\lambda ^2} + 1 - 2\lambda \sigma \upsilon \nu x} \right)\sqrt {{\lambda ^2} + 1 - 2\lambda \sigma \upsilon \nu x} }}$ και μηδενίζεται όταν $\displaystyle x = 0\;\;\; \vee \;\;\;\sigma \upsilon \nu x = \lambda \;\;\; \vee \;\;x = \pi$ .

Μελετώντας το πρόσημο της παραγώγου της, βλέπουμε ότι η συνάρτηση

παρουσιάζει ελάχιστο όταν $\displaystyle \sigma \upsilon \nu x = \lambda$ . Όταν το συνημίτονο πάρει την ελάχιστη τιμή του έχουμε τη μέγιστη γωνία.

Για την τιμή $\displaystyle \sigma \upsilon \nu \theta = \lambda = \left( {{\rm O}{\rm A}} \right)$ , στο τρίγωνο MAO

είναι $\displaystyle {\rm A}{{\rm M}^2} = {\rm O}{{\rm A}^2} + {\rm O}{{\rm M}^2} - 2{\rm O}{\rm A} \cdot {\rm O}{\rm M}\sigma \upsilon \nu \theta$

$\displaystyle \Leftrightarrow {\rm A}{{\rm M}^2} = 1 + {\lambda ^2} - 2{\lambda ^2} = 1 - {\lambda ^2} = {\rm O}{{\rm M}^2} - {\rm O}{{\rm A}^2}$

άρα ισχύει το Πυθαγόρειο Θεώρημα, οπότε είναι ορθογώνιο με $\displaystyle \widehat {{\rm M}{\rm A}{\rm O}} = 90^\circ$ .

S.E.Louridas · #9

Μετά τις εκπληκτικές παρεμβάσεις των συναδέλφων και φίλων, ας δούμε και μία μέθοδο κατασκευαστικής επίλυσης που λειτουργεί τελικά για δύο τυχόντα σημεία O,A

που όμως και τα δύο να είναι εσωτερικά του κύκλου ή και τα δύο να είναι εξωτερικά του κύκλου. Πάντα και σταθερά μόνο για λόγους πολυφωνίας εδώ στο mathematica.

Θεωρούμε τυχόντα κύκλο ${c_1}$ που διέρχεται από τα A,O

και τέμνει τον δεδομένο κύκλο

στα σημεία V,{V{'}}.

Η τομή των ευθειών

και

δίνει το ριζικό κέντρο

της δέσμης των κύκλων που διέρχονται από τα σημεία A,O.

Είναι πλέον καθαρό ότι για τον τυχόντα κύκλο

που διέρχεται από τα A,O

η εφαπτόμενη του

ισούται με την εφαπτόμενη

του κύκλου

Tο τρίγωνο SML

είναι ισοσκελές και επειδή οι παρά τη βάση του γωνίες είναι ίσες και οξείες, το κέντρο του {K{'}}

επί της μεσοκαθέτου του

θα απέχει μεγαλύτερη απόσταση από το

(μέσο του

) από την απόσταση του κέντρου

του εφαπτόμενου κύκλου

στον

. Άρα $KM \leqslant L{K{'}}$ . Άρα ο κύκλος με την ελάχιστη ακτίνα που διέρχεται από τα σημεία A,O

είναι ο εφαπτόμενος

στον

και στο σημείο

και αυτό απαντά στο ερώτημα, καθότι τότε η αντίστοιχη επίκεντρη γωνία $\angle AKO$ , στον εφαπτόμενο κύκλο

καθίσταται μέγιστη.

(*) Ο κύκλος

είναι ο με τη μικρότερη ακτίνα από τους δύο εφαπτόμενους στον δεδομένο κύκλο

αν αυτοί είναι άνισων ακτίνων, που διέρχονται από τα σημεία O,A.

(**) Για τη κατασκευή του

με την ιδιότητα που μας ζητούν, μόλις προσδιορίσουμε το

με το να θεωρήσουμε τον τυχόντα κύκλο c_1

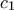όπως είδαμε, αρκεί να φέρουμε την εφαπτόμενη

στον δεδομένο κύκλο

και να πάρουμε την γωνία $\angle AMO.$

(***) Εδώ στην ειδική περίπτωση που είδαμε και επειδή το

είναι κέντρο, προκύπτει ότι το τρίγωνο MAO

είναι ορθογώνιο στην κορυφή

(****) Αν τα σημεία είναι O,A

είναι σε θέση, ώστε το ένα να είναι εντός του κύκλου

και το άλλο εκτός αυτού, τότε το

προσδιορίζεται ως τομή της ευθείας

με τον κύκλο

, όπου ως ευκλείδεια γωνία (κυρτή) αυτή μεγιστοποιείται όταν είναι $\pi$ . To

στη περίπτωση αυτή είναι εσωτερικό σημείο του ευθύγραμμου τμήματος OA.

Μεγιστοποίηση γωνίας

Μεγιστοποίηση γωνίας

Re: Μεγιστοποίηση γωνίας

Re: Μεγιστοποίηση γωνίας

Re: Μεγιστοποίηση γωνίας

Re: Μεγιστοποίηση γωνίας

Re: Μεγιστοποίηση γωνίας

Re: Μεγιστοποίηση γωνίας

Re: Μεγιστοποίηση γωνίας

Re: Μεγιστοποίηση γωνίας

Μέλη σε σύνδεση