 θετικοί ακέραιοι. Η διαφορά μεταξύ κάθε δύο διαδοχικών αριθμών ισούται με τον μέγιστο κοινό διαιρέτη τους. Να βρεθεί το μέγιστο
θετικοί ακέραιοι. Η διαφορά μεταξύ κάθε δύο διαδοχικών αριθμών ισούται με τον μέγιστο κοινό διαιρέτη τους. Να βρεθεί το μέγιστο  ώστε ο
ώστε ο  να διαιρεί το γινόμενο των
να διαιρεί το γινόμενο των  αριθμών ανεξάρτητα από το ποιοι είναι αυτοί οι αριθμοί
αριθμών ανεξάρτητα από το ποιοι είναι αυτοί οι αριθμοίΣυντονιστές: cretanman, silouan, rek2
 θετικοί ακέραιοι. Η διαφορά μεταξύ κάθε δύο διαδοχικών αριθμών ισούται με τον μέγιστο κοινό διαιρέτη τους. Να βρεθεί το μέγιστο
θετικοί ακέραιοι. Η διαφορά μεταξύ κάθε δύο διαδοχικών αριθμών ισούται με τον μέγιστο κοινό διαιρέτη τους. Να βρεθεί το μέγιστο  ώστε ο
ώστε ο  να διαιρεί το γινόμενο των
να διαιρεί το γινόμενο των  αριθμών ανεξάρτητα από το ποιοι είναι αυτοί οι αριθμοί
αριθμών ανεξάρτητα από το ποιοι είναι αυτοί οι αριθμοί σημεία στην περιφέρεια του κύκλου.
σημεία στην περιφέρεια του κύκλου. .
. (μ'αυτή τη σειρά) στην περιφέρεια του κύκλου.Το γινόμενό τους είναι
(μ'αυτή τη σειρά) στην περιφέρεια του κύκλου.Το γινόμενό τους είναι  .
. (μ'αυτή τη σειρά) στην περιφέρεια του κύκλου.Το γινόμενό τους είναι
(μ'αυτή τη σειρά) στην περιφέρεια του κύκλου.Το γινόμενό τους είναι  .
. .
. διαιρεί πάντα το γινόμενο των αριθμών στην περιφέρεια του κύκλου,οπότε θα είναι και το ζητούμενο (λόγω της προηγούμενης).
διαιρεί πάντα το γινόμενο των αριθμών στην περιφέρεια του κύκλου,οπότε θα είναι και το ζητούμενο (λόγω της προηγούμενης). .Αν όχι,τότε τα πιθανά υπόλοιπα είναι
.Αν όχι,τότε τα πιθανά υπόλοιπα είναι 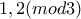 .Από την αρχική παρατήρηση αυτά πρέπει να εμφανίζονται εναλλάξ.Όμως,επειδή το πλήθος των αριθμών είναι περιττό,αυτό είναι αδύνατο,συνεπώς κάποιος διαιρείται με το
.Από την αρχική παρατήρηση αυτά πρέπει να εμφανίζονται εναλλάξ.Όμως,επειδή το πλήθος των αριθμών είναι περιττό,αυτό είναι αδύνατο,συνεπώς κάποιος διαιρείται με το  .
. αριθμοί θα πρέπει να είναι άρτιοι(αλλιώς θα εμφανίζονταν διαδοχικοί περιττοί).Επιπλέον,θα υπάρχουν δύο διαδοχικοί που θα είναι και οι δύο άρτιοι(αφού είναι τουλάχιστον
αριθμοί θα πρέπει να είναι άρτιοι(αλλιώς θα εμφανίζονταν διαδοχικοί περιττοί).Επιπλέον,θα υπάρχουν δύο διαδοχικοί που θα είναι και οι δύο άρτιοι(αφού είναι τουλάχιστον  το πλήθος),άρα κάποιος απ αυτούς τους δύο θα διαιρείται με το
το πλήθος),άρα κάποιος απ αυτούς τους δύο θα διαιρείται με το  (διαφορετικά η διαφορά τους θα διαιρούνταν με το 4 ενώ οι αριθμοί όχι).Μετρώντας,τώρα,τα δυάρια βρίσκουμε τουλάχιστον
(διαφορετικά η διαφορά τους θα διαιρούνταν με το 4 ενώ οι αριθμοί όχι).Μετρώντας,τώρα,τα δυάρια βρίσκουμε τουλάχιστον  ,άρα το γινόμενο είναι διαιρετό με
,άρα το γινόμενο είναι διαιρετό με  .
.Εδώ υπάρχει ένα λαθάκι. Δεν μπορούν δυο μη πολλαπλάσια του 3 να αφήνουν το ίδιο υπόλοιπο διαιρούμενοι με τοAntonis_Z έγραψε: δε γίνεται δύο διαδοχικοί αριθμοί(της περιφέρειας) να είναι και οι δύο περιττοί ή και οι δύο να αφήνουν το ίδιο υπόλοιπο διαιρούμενοι με το.
 . Αργότερα βέβαια το χρησιμοποιείς σωστά.
. Αργότερα βέβαια το χρησιμοποιείς σωστά.  πιάνεται είναι η διάταξη
πιάνεται είναι η διάταξη  . Το γινόμενο εδώ είναι ακριβώς
. Το γινόμενο εδώ είναι ακριβώς  .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες