JBMO 2017
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
Re: JBMO 2017
ΑΠΟΤΕΛΕΣΜΑΤΑ
ΝΤΟΚΑΣ ΧΑΛΚΙΝΟ
ΛΙΓΝΟΣ ΧΑΛΚΙΝΟ
ΑΔΑΜΟΠΟΥΛΟΣ ΧΑΛΚΙΝΟ
ΜΑΡΓΑΡΙΤΗΣ ΧΑΛΚΙΝΟ
ΣΚΟΥΛΑΡΙΚΗΣ ΧΑΛΚΙΝΟ
ΣΥΓΧΑΡΗΤΗΡΙΑ ΣΕ ΟΛΑ ΤΑ ΠΑΙΔΙΑ
ΝΤΟΚΑΣ ΧΑΛΚΙΝΟ
ΛΙΓΝΟΣ ΧΑΛΚΙΝΟ
ΑΔΑΜΟΠΟΥΛΟΣ ΧΑΛΚΙΝΟ
ΜΑΡΓΑΡΙΤΗΣ ΧΑΛΚΙΝΟ
ΣΚΟΥΛΑΡΙΚΗΣ ΧΑΛΚΙΝΟ
ΣΥΓΧΑΡΗΤΗΡΙΑ ΣΕ ΟΛΑ ΤΑ ΠΑΙΔΙΑ
Re: JBMO 2017
thanos59 έγραψε:ΑΠΟΤΕΛΕΣΜΑΤΑ
ΝΤΟΚΑΣ ΧΑΛΚΙΝΟ
ΛΙΓΝΟΣ ΧΑΛΚΙΝΟ
ΑΔΑΜΟΠΟΥΛΟΣ ΧΑΛΚΙΝΟ
ΜΑΡΓΑΡΙΤΗΣ ΧΑΛΚΙΝΟ
ΣΚΟΥΛΑΡΙΚΗΣ ΧΑΛΚΙΝΟ
ΣΥΓΧΑΡΗΤΗΡΙΑ ΣΕ ΟΛΑ ΤΑ ΠΑΙΔΙΑ
Re: JBMO 2017
Τα αποτελέσματα της αποστολής της Κύπρου είναι:
Θεοχάρους Στέφανος (Αργυρό μετάλλιο)
Χαραλάμπους Ιωάννης (Χάλκινο μετάλλιο)
Θεοδούλου Αχιλλέας-Αλέξανδρος (Χάλκινο μετάλλιο)
Seyed Datis Amir Kalali
Γεωργίου Χαράλαμπος
Παπαχριστοδούλου Γιώργος
Συγχαρητήρια παιδιά για αυτή την ωραία εμφάνιση. Θέλω να ευχαριστήσω ιδιαίτερα τους Ματθαίου Κυριάκο (Αρχηγός) και Ευαγόρου Αναστάσιο (Υπαρχηγό), οι οποίοι (αν και "πρωτάρηδες" σε JBMO) έκαναν εξαιρετική δουλειά, αλλά και όλους τους συναδέλφους της Κυπριακής Μαθηματικής Εταιρείας που προετοίμασαν τα παιδιά για τον διαγωνισμό αυτό.
Επίσης, θέλω να συγχαρώ την αποστολή της Ελλάδας για τα 5 χάλκινα μετάλλια που κατάφεραν τα παιδιά να μας χαρίσουν, καθώς επίσης και τους Συγκελάκη Αλέξανδρο (Αρχηγό) και Πούλο Ανδρέα (Υπαρχηγό) για την εξαιρετική δουλειά με τα παιδιά.
Να σας ενημερώσω ότι τα cut offs για τα μετάλλια ήταν 35 για το Χρυσό, 19 για το Αργυρό και 9 για το Χάλκινο. Είμαι βέβαιος ότι θα ακολουθήσει ανάρτηση του φίλτατου Αλέξανδρου με περισσότερες λεπτομέρειες.
Ξανά πολλά μπράβο σε όλους. Μας κάνατε περήφανους!!!
Θεοχάρους Στέφανος (Αργυρό μετάλλιο)
Χαραλάμπους Ιωάννης (Χάλκινο μετάλλιο)
Θεοδούλου Αχιλλέας-Αλέξανδρος (Χάλκινο μετάλλιο)
Seyed Datis Amir Kalali
Γεωργίου Χαράλαμπος
Παπαχριστοδούλου Γιώργος
Συγχαρητήρια παιδιά για αυτή την ωραία εμφάνιση. Θέλω να ευχαριστήσω ιδιαίτερα τους Ματθαίου Κυριάκο (Αρχηγός) και Ευαγόρου Αναστάσιο (Υπαρχηγό), οι οποίοι (αν και "πρωτάρηδες" σε JBMO) έκαναν εξαιρετική δουλειά, αλλά και όλους τους συναδέλφους της Κυπριακής Μαθηματικής Εταιρείας που προετοίμασαν τα παιδιά για τον διαγωνισμό αυτό.
Επίσης, θέλω να συγχαρώ την αποστολή της Ελλάδας για τα 5 χάλκινα μετάλλια που κατάφεραν τα παιδιά να μας χαρίσουν, καθώς επίσης και τους Συγκελάκη Αλέξανδρο (Αρχηγό) και Πούλο Ανδρέα (Υπαρχηγό) για την εξαιρετική δουλειά με τα παιδιά.
Να σας ενημερώσω ότι τα cut offs για τα μετάλλια ήταν 35 για το Χρυσό, 19 για το Αργυρό και 9 για το Χάλκινο. Είμαι βέβαιος ότι θα ακολουθήσει ανάρτηση του φίλτατου Αλέξανδρου με περισσότερες λεπτομέρειες.
Ξανά πολλά μπράβο σε όλους. Μας κάνατε περήφανους!!!
Σωτήρης Λοϊζιάς
-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: JBMO 2017
Συγχαρητήρια στα παιδιά! Θα τους έφαγε η γεωμετρία τους δικούς μας με το σχήμα.
Γιάννης Μπορμπαντωνάκης
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: JBMO 2017
Πολλά ειλικρινή συγχαρητήρια στους Έλληνες και τους αδελφούς Κύπριους και καλή επάνοδο.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ
- Επιμελητής
- Δημοσιεύσεις: 1172
- Εγγραφή: Τετ Δεκ 31, 2008 8:07 pm
- Τοποθεσία: ΗΡΑΚΛΕΙΟ ΚΡΗΤΗΣ
Re: JBMO 2017
Πολλά συγχαρητήρια στις ομάδες μας Ελλάδας και Κύπρου για τις μεγάλες επιτυχίες σε μία δύσκολη μάχη!
-
Panagiotis11
- Δημοσιεύσεις: 73
- Εγγραφή: Κυρ Απρ 09, 2017 7:33 pm
- Τοποθεσία: Πάτρα
Re: JBMO 2017
Συγχαρητήρια στα παιδιά της ελληνικής και κυπριακής αποστολής αλλα κυρίως στον Ορέστη Λιγνό και τον Διονύσιο Αδαμόπουλο που είναι μέλη του 
Μπορεί να απογοητευθείς αν αποτύχεις, αλλά είσαι χαμένος αν δεν προσπαθήσεις.
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: JBMO 2017
Καλησπέρα σε όλους από τη Βάρνα!!
Σήμερα ήταν η συνεδρίαση των αρχηγών για την αποδοχή της βαθμολογίας που έγινε σήμερα το πρωί και για την κατανομή των μεταλλίων!
Η Ελληνική Αποστολή κατέκτησε 5 χάλκινα μετάλλια, όπως ήδη σημειώθηκε, και η Κυπριακή 1 αργυρό και 2 χάλκινα!
Θέλω να δώσω ΠΟΛΛΑ συγχαρητήρια σε όλους τους μαθητές Ελλάδας και Κύπρου που αντεπεξήλθαν σε τόσο δύσκολα θέματα και κατάφεραν να κατακτήσουν μετάλλιο, αλλά και στον Στέργιο Μάστορη (και στα αντίστοιχα παιδιά της Κύπρου) που δεν κατάφερε τελικά να είναι ανάμεσα σε εκείνους που θα βραβευθούν αύριο. Παρόλα αυτά είμαι σίγουρος για το λαμπρό του μέλλον!! Πολλοί σπουδαίοι επιστήμονες (είτε στα μαθηματικά είτε σε άλλους τομείς) δεν μπορούν εύκολα να αποδώσουν το μέγιστο των δυνατοτήτων τους υπό την πίεση χρόνου!
Οι σκέψεις, οι ιδέες και τα πρόχειρα των μαθητών μας κατά τη διάρκεια του διαγωνισμού ήταν πάρα πολλά και τα θέματα δύσκολα και πρωτότυπα.
Χάρηκα ιδιαίτερα που ήμουν αρχηγός αυτής της αποστολής καθώς όλα τα παιδιά που γνώρισα ήταν εξαιρετικά (όχι μόνο στα μαθηματικά αλλά και στους τρόπους, στη συμπεριφορά, στο ήθος τους...) Να τα χαίρονται οι γονείς τους!!
Ευχαριστώ πολύ και τον αγαπητό συνάδελφο και φίλο Ανδρέα Πούλο για την άψογη συνεργασία που είχαμε καθ'όλη τη διάρκεια της διοργάνωσης!
Τελειώνω με μία ελαφρά τροποποιημένη λύση του Ευθύμη Ντόκα (την οποία έγραψε κατά τη διάρκεια του διαγωνισμού) στην ανισότητα η οποία (παρά το ότι είχε αρκετές πράξεις και περιπτώσεις) μου άρεσε.
 κι επειδή είναι ακέραιοι, άρα
κι επειδή είναι ακέραιοι, άρα 
Η ανισότητα γράφεται

και διαιρώντας με παίρνουμε
παίρνουμε

Διακρίνουμε τώρα τις εξής περιπτώσεις:
Α) Αν και
και  (το ότι ισχύει
(το ότι ισχύει  προκύπτει από την
προκύπτει από την  )
)
τότε λόγω της ανισότητας και προσθέτοντας όλες τις κυκλικές που προκύπτουν καταλήγουμε στη ζητούμενη
και προσθέτοντας όλες τις κυκλικές που προκύπτουν καταλήγουμε στη ζητούμενη 
B) Αν δεν ισχύει η Α) τότε έχουμε είτε
είτε  .
.
a) Αν τότε αντικαθιστώντας στην αρχική και κάνοντας πράξεις καταλήγουμε στην
τότε αντικαθιστώντας στην αρχική και κάνοντας πράξεις καταλήγουμε στην
 και αφού
και αφού  άρα θέτοντας
άρα θέτοντας  παίρνουμε:
παίρνουμε:
 που ισχύει. Η ισότητα ισχύει αν και μόνο αν
που ισχύει. Η ισότητα ισχύει αν και μόνο αν  δηλαδή
δηλαδή  άρα όταν
άρα όταν 
b) Αν τότε αντικαθιστώντας στην αρχική και κάνοντας πράξεις καταλήγουμε στην
τότε αντικαθιστώντας στην αρχική και κάνοντας πράξεις καταλήγουμε στην
 και αφού
και αφού  άρα θέτοντας
άρα θέτοντας  παίρνουμε
παίρνουμε  που ισχύει. Η ισότητα ισχύει αν και μόνο αν
που ισχύει. Η ισότητα ισχύει αν και μόνο αν  δηλαδή
δηλαδή  άρα όταν
άρα όταν 
******************************************************
Παιδιά σας εύχομαι τα καλύτερα! Και του χρόνου...
Αλέξανδρος
Σήμερα ήταν η συνεδρίαση των αρχηγών για την αποδοχή της βαθμολογίας που έγινε σήμερα το πρωί και για την κατανομή των μεταλλίων!
Η Ελληνική Αποστολή κατέκτησε 5 χάλκινα μετάλλια, όπως ήδη σημειώθηκε, και η Κυπριακή 1 αργυρό και 2 χάλκινα!
Θέλω να δώσω ΠΟΛΛΑ συγχαρητήρια σε όλους τους μαθητές Ελλάδας και Κύπρου που αντεπεξήλθαν σε τόσο δύσκολα θέματα και κατάφεραν να κατακτήσουν μετάλλιο, αλλά και στον Στέργιο Μάστορη (και στα αντίστοιχα παιδιά της Κύπρου) που δεν κατάφερε τελικά να είναι ανάμεσα σε εκείνους που θα βραβευθούν αύριο. Παρόλα αυτά είμαι σίγουρος για το λαμπρό του μέλλον!! Πολλοί σπουδαίοι επιστήμονες (είτε στα μαθηματικά είτε σε άλλους τομείς) δεν μπορούν εύκολα να αποδώσουν το μέγιστο των δυνατοτήτων τους υπό την πίεση χρόνου!
Οι σκέψεις, οι ιδέες και τα πρόχειρα των μαθητών μας κατά τη διάρκεια του διαγωνισμού ήταν πάρα πολλά και τα θέματα δύσκολα και πρωτότυπα.
Χάρηκα ιδιαίτερα που ήμουν αρχηγός αυτής της αποστολής καθώς όλα τα παιδιά που γνώρισα ήταν εξαιρετικά (όχι μόνο στα μαθηματικά αλλά και στους τρόπους, στη συμπεριφορά, στο ήθος τους...) Να τα χαίρονται οι γονείς τους!!
Ευχαριστώ πολύ και τον αγαπητό συνάδελφο και φίλο Ανδρέα Πούλο για την άψογη συνεργασία που είχαμε καθ'όλη τη διάρκεια της διοργάνωσης!
Τελειώνω με μία ελαφρά τροποποιημένη λύση του Ευθύμη Ντόκα (την οποία έγραψε κατά τη διάρκεια του διαγωνισμού) στην ανισότητα η οποία (παρά το ότι είχε αρκετές πράξεις και περιπτώσεις) μου άρεσε.
Λόγω συμμετρίας μπορούμε να υποθέσουμε ότιthanos59 έγραψε:
Πρόβλημα 2: Έστωθετικοί ακέραιοι τέτοιο ώστε
. Να δείξετε ότι
 κι επειδή είναι ακέραιοι, άρα
κι επειδή είναι ακέραιοι, άρα 
Η ανισότητα γράφεται

και διαιρώντας με
 παίρνουμε
παίρνουμε 
Διακρίνουμε τώρα τις εξής περιπτώσεις:
Α) Αν
 και
και  (το ότι ισχύει
(το ότι ισχύει  προκύπτει από την
προκύπτει από την  )
)τότε λόγω της ανισότητας
 και προσθέτοντας όλες τις κυκλικές που προκύπτουν καταλήγουμε στη ζητούμενη
και προσθέτοντας όλες τις κυκλικές που προκύπτουν καταλήγουμε στη ζητούμενη 
B) Αν δεν ισχύει η Α) τότε έχουμε
 είτε
είτε  .
. a) Αν
 τότε αντικαθιστώντας στην αρχική και κάνοντας πράξεις καταλήγουμε στην
τότε αντικαθιστώντας στην αρχική και κάνοντας πράξεις καταλήγουμε στην  και αφού
και αφού  άρα θέτοντας
άρα θέτοντας  παίρνουμε:
παίρνουμε: που ισχύει. Η ισότητα ισχύει αν και μόνο αν
που ισχύει. Η ισότητα ισχύει αν και μόνο αν  δηλαδή
δηλαδή  άρα όταν
άρα όταν 
b) Αν
 τότε αντικαθιστώντας στην αρχική και κάνοντας πράξεις καταλήγουμε στην
τότε αντικαθιστώντας στην αρχική και κάνοντας πράξεις καταλήγουμε στην  και αφού
και αφού  άρα θέτοντας
άρα θέτοντας  παίρνουμε
παίρνουμε  που ισχύει. Η ισότητα ισχύει αν και μόνο αν
που ισχύει. Η ισότητα ισχύει αν και μόνο αν  δηλαδή
δηλαδή  άρα όταν
άρα όταν 
******************************************************
Παιδιά σας εύχομαι τα καλύτερα! Και του χρόνου...
Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: JBMO 2017
Συγχαρητήρα στα παιδιά, στους συνοδούς, στους γονείς τους, στους δασκάλους τους και σε όλους, όσοι συνέβαλαν σε αυτή την ωραία εμφάνιση !!!
Εύχομαι στους μικρότερους να διαπρέψουν και του χρόνου, ενώ σε όσους θα έρθουν στο Λύκειο, να μπούνε στην ομάδα ΙΜΟ !!!
Συγχαρητήρια και ευχές για διακρίσεις δίνω και στην ομάδα της Κύπρου !!!
Καλό καλοκαίρι και καλή ξεκούραση !!!
Εύχομαι στους μικρότερους να διαπρέψουν και του χρόνου, ενώ σε όσους θα έρθουν στο Λύκειο, να μπούνε στην ομάδα ΙΜΟ !!!
Συγχαρητήρια και ευχές για διακρίσεις δίνω και στην ομάδα της Κύπρου !!!
Καλό καλοκαίρι και καλή ξεκούραση !!!
-
Κατερινόπουλος Νικόλας
- Δημοσιεύσεις: 659
- Εγγραφή: Κυρ Μαρ 05, 2017 3:24 pm
- Τοποθεσία: Καλαμάτα, Μεσσηνία
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: JBMO 2017
Συγχαρητήρια στα παιδιά και της Ελλάδας και της Κύπρου. Ελπίζω και εύχομαι τις επόμενες χρονιές να έχουν ακόμα καλύτερα αποτελέσματα.
«Είναι φυσικό να χαίρεσαι με την επιτυχία στις ολυμπιάδες ακόμη κα να αισθάνεσαι περήφανος. Η μη επιτυχία δε, δεν πρέπει να μας αναστατώνει υπερβολικά»…
«Για να επιτύχεις στις ολυμπιάδες, χρειάζονται μερικά ειδικού τύπου χαρίσματα, τα οποία δεν είναι κατά ανάγκη απαραίτητα για την επιτυχή ερευνητική εργασία (επιστημονική μελέτη). Ήδη η καθαυτή παρουσία του χρονικού περιορισμού για να λύσεις τα προβλήματα πολλούς τους καθιστά εντελώς ανήμπορους. Αλλά υπάρχουν επίσης μαθηματικά προβλήματα τα οποία μπορούν να λυθούν μόνο ως αποτέλεσμα πολύ μεγάλης σε διάρκεια σκέψης και διατύπωσης νεών εννοιών. Πολλά τέτοια προβλήματα είχαν λυθεί από τον αξιόλογο σοβιετικό τοπολογιστή Αλεξάντροβ. Και όχι τυχαία ο Πάβελ Σεργκέϊβιτς (Αλεξάντροβ) έλεγε ότι αν υπήρχαν ολυμπιάδες όταν ήταν νέος, πιθανόν να μη γινόταν μαθηματικός: τα κύρια επιτεύγματά του στα μαθηματικά δεν ήταν καρπός γρήγορης ευφυΐας, αλλά αποτέλεσμα μακρούς και σε βάθος διαλογισμού (σκέψης)»
Για να ενισχύσουμε τα παραπάνω λόγια του Αλέξανδρου, με επίκληση στην αυθεντία όπως θα έλεγε το βιβλίο της έκθεσης. Περισσότερο για τα παιδιά που δεν φθάνουν καν σε αυτό το επίπεδο και ίσως να απογοητεύονται. Παραθέτω ένα κομμάτι από την εισαγωγή του βιβλίου Μαθηματικές Ολυμπιάδες Μόσχας 1993-2005. Προλογίζει ο Τιχομίροβ και αναφέρει τα παρακάτω λόγια του Κολμογκόροβ.cretanman έγραψε:Πολλοί σπουδαίοι επιστήμονες (είτε στα μαθηματικά είτε σε άλλους τομείς) δεν μπορούν εύκολα να αποδώσουν το μέγιστο των δυνατοτήτων τους υπό την πίεση χρόνου!
«Είναι φυσικό να χαίρεσαι με την επιτυχία στις ολυμπιάδες ακόμη κα να αισθάνεσαι περήφανος. Η μη επιτυχία δε, δεν πρέπει να μας αναστατώνει υπερβολικά»…
«Για να επιτύχεις στις ολυμπιάδες, χρειάζονται μερικά ειδικού τύπου χαρίσματα, τα οποία δεν είναι κατά ανάγκη απαραίτητα για την επιτυχή ερευνητική εργασία (επιστημονική μελέτη). Ήδη η καθαυτή παρουσία του χρονικού περιορισμού για να λύσεις τα προβλήματα πολλούς τους καθιστά εντελώς ανήμπορους. Αλλά υπάρχουν επίσης μαθηματικά προβλήματα τα οποία μπορούν να λυθούν μόνο ως αποτέλεσμα πολύ μεγάλης σε διάρκεια σκέψης και διατύπωσης νεών εννοιών. Πολλά τέτοια προβλήματα είχαν λυθεί από τον αξιόλογο σοβιετικό τοπολογιστή Αλεξάντροβ. Και όχι τυχαία ο Πάβελ Σεργκέϊβιτς (Αλεξάντροβ) έλεγε ότι αν υπήρχαν ολυμπιάδες όταν ήταν νέος, πιθανόν να μη γινόταν μαθηματικός: τα κύρια επιτεύγματά του στα μαθηματικά δεν ήταν καρπός γρήγορης ευφυΐας, αλλά αποτέλεσμα μακρούς και σε βάθος διαλογισμού (σκέψης)»
Re: JBMO 2017
Εναλλακτικά για την ανισότητα:Λόγω της συμμετρίας υποθέτουμε
 .
.
 Άν ισχύει η ανισότητα για μια τριάδα
Άν ισχύει η ανισότητα για μια τριάδα  τότε αποδεικνύω ότι ισχύει και για την
τότε αποδεικνύω ότι ισχύει και για την  και επομένως και για όλες της τριάδες
και επομένως και για όλες της τριάδες  .Για το παραπάνω αρκεί
.Για το παραπάνω αρκεί  ή
ή  το οποίο ισχύει λόγω του ότι
το οποίο ισχύει λόγω του ότι  .
.
 Έπειτα αποδεικνύουμε ότι η ανισότητα ισχύει για όλες τις τριάδες
Έπειτα αποδεικνύουμε ότι η ανισότητα ισχύει για όλες τις τριάδες  και λόγω και του παραπάνω αποτελέσματος θα ισχύει για όλα τα
και λόγω και του παραπάνω αποτελέσματος θα ισχύει για όλα τα  .Το τελευταίο αποδεικνύεται και επαγωγικά(παρόμοια με το πρώτο αποτέλεσμα μόνο που τώρα μειώνουμε το
.Το τελευταίο αποδεικνύεται και επαγωγικά(παρόμοια με το πρώτο αποτέλεσμα μόνο που τώρα μειώνουμε το 
):Αρχικά είναι εύκολο να βρεθεί ότι ισχύει η ανισότητα(ισότητα) για όλες της τριάδες .
.
 Υποθέτοντας ότι ισχύει για μια τριάδα
Υποθέτοντας ότι ισχύει για μια τριάδα  για να δείξουμε ότι ισχύει και για την
για να δείξουμε ότι ισχύει και για την  (χρησιμοποιώντας κλασικά την υπόθεση βγαίνει ότι αρκεί
(χρησιμοποιώντας κλασικά την υπόθεση βγαίνει ότι αρκεί  το οποίο ισχύει. (αν έχουν γίνει σωστά η πράξεις)).Άρα θα ισχύει η ανισότητα για κάθε τριάδα
το οποίο ισχύει. (αν έχουν γίνει σωστά η πράξεις)).Άρα θα ισχύει η ανισότητα για κάθε τριάδα 
Μέσω παραδείγματος, αν είναι να αποδείξουμε ότι η ανισότητα ισχύει πχ για την τριάδα ,εργαζόμαστε ως εξής:Η ισότητα γνωρίζουμε ότι ισχύει για την
,εργαζόμαστε ως εξής:Η ισότητα γνωρίζουμε ότι ισχύει για την  ενώ από το
ενώ από το  θα ισχύει και για την
θα ισχύει και για την  .Τέλος,αν αυξήσουμε τον μεγαλύτερο αριθμό η ανισότητα θα συνεχίσει να ισχύει
.Τέλος,αν αυξήσουμε τον μεγαλύτερο αριθμό η ανισότητα θα συνεχίσει να ισχύει  οπότε θα ισχύει και για την τριάδα
οπότε θα ισχύει και για την τριάδα  ...
...
 .
. Άν ισχύει η ανισότητα για μια τριάδα
Άν ισχύει η ανισότητα για μια τριάδα  τότε αποδεικνύω ότι ισχύει και για την
τότε αποδεικνύω ότι ισχύει και για την  και επομένως και για όλες της τριάδες
και επομένως και για όλες της τριάδες  .Για το παραπάνω αρκεί
.Για το παραπάνω αρκεί  ή
ή  το οποίο ισχύει λόγω του ότι
το οποίο ισχύει λόγω του ότι  .
. Έπειτα αποδεικνύουμε ότι η ανισότητα ισχύει για όλες τις τριάδες
Έπειτα αποδεικνύουμε ότι η ανισότητα ισχύει για όλες τις τριάδες  και λόγω και του παραπάνω αποτελέσματος θα ισχύει για όλα τα
και λόγω και του παραπάνω αποτελέσματος θα ισχύει για όλα τα  .Το τελευταίο αποδεικνύεται και επαγωγικά(παρόμοια με το πρώτο αποτέλεσμα μόνο που τώρα μειώνουμε το
.Το τελευταίο αποδεικνύεται και επαγωγικά(παρόμοια με το πρώτο αποτέλεσμα μόνο που τώρα μειώνουμε το 
):Αρχικά είναι εύκολο να βρεθεί ότι ισχύει η ανισότητα(ισότητα) για όλες της τριάδες
 .
. Υποθέτοντας ότι ισχύει για μια τριάδα
Υποθέτοντας ότι ισχύει για μια τριάδα  για να δείξουμε ότι ισχύει και για την
για να δείξουμε ότι ισχύει και για την  (χρησιμοποιώντας κλασικά την υπόθεση βγαίνει ότι αρκεί
(χρησιμοποιώντας κλασικά την υπόθεση βγαίνει ότι αρκεί  το οποίο ισχύει. (αν έχουν γίνει σωστά η πράξεις)).Άρα θα ισχύει η ανισότητα για κάθε τριάδα
το οποίο ισχύει. (αν έχουν γίνει σωστά η πράξεις)).Άρα θα ισχύει η ανισότητα για κάθε τριάδα 
Μέσω παραδείγματος, αν είναι να αποδείξουμε ότι η ανισότητα ισχύει πχ για την τριάδα
 ,εργαζόμαστε ως εξής:Η ισότητα γνωρίζουμε ότι ισχύει για την
,εργαζόμαστε ως εξής:Η ισότητα γνωρίζουμε ότι ισχύει για την  ενώ από το
ενώ από το  θα ισχύει και για την
θα ισχύει και για την  .Τέλος,αν αυξήσουμε τον μεγαλύτερο αριθμό η ανισότητα θα συνεχίσει να ισχύει
.Τέλος,αν αυξήσουμε τον μεγαλύτερο αριθμό η ανισότητα θα συνεχίσει να ισχύει  οπότε θα ισχύει και για την τριάδα
οπότε θα ισχύει και για την τριάδα  ...
...-
Datis-Kalali
- Δημοσιεύσεις: 117
- Εγγραφή: Δευ Δεκ 12, 2016 5:33 pm
- Τοποθεσία: Λευκωσία
Ανισότητα, ισχυεί η όχι;
Βαλκανίαδα Νέων 2017, Πρόβλημα
Έστω θετικοί ακέραιοι τέτοιο ώστε
θετικοί ακέραιοι τέτοιο ώστε 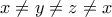 . Να δείξετε ότι
. Να δείξετε ότι

Πότε ισχύει η ισότητα;
Το λύση μου στον διαγωνισμό
Χώρις βλαβή τις γενναιότητας θέτουμε
Τωρά αν έχουμε
έχουμε  : (1)
: (1)
και η ανισότητα γράφεται
Απο την ανισότητα AM/GM
Αρκεί να δείξουμε ότι
που είναι φανερός.
Η ισότητα ισχυεί αν και μόνον αν , δηλαδή όταν
, δηλαδή όταν  και
και  είναι διαδοχικοί.
είναι διαδοχικοί.
Μπορείτε να μου βοηθήσετε και να το διορθώσετε παρακαλώ;
Έστω
 θετικοί ακέραιοι τέτοιο ώστε
θετικοί ακέραιοι τέτοιο ώστε 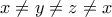 . Να δείξετε ότι
. Να δείξετε ότι
Πότε ισχύει η ισότητα;
Το λύση μου στον διαγωνισμό
Χώρις βλαβή τις γενναιότητας θέτουμε

Τωρά αν
 έχουμε
έχουμε  : (1)
: (1)και η ανισότητα γράφεται

Απο την ανισότητα AM/GM

Αρκεί να δείξουμε ότι

που είναι φανερός.
Η ισότητα ισχυεί αν και μόνον αν
 , δηλαδή όταν
, δηλαδή όταν  και
και  είναι διαδοχικοί.
είναι διαδοχικοί.Μπορείτε να μου βοηθήσετε και να το διορθώσετε παρακαλώ;
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Ανισότητα, ισχυεί η όχι;
Δεν βλέπω πρόβλημα. Όλα σωστά μου φαίνονται.Datis-Kalali έγραψε: έχουμε: (1)
...
Αρκεί να δείξουμε ότι
που είναι φανερός.
Η ισότητα ισχυεί αν και μόνον αν, δηλαδή όταν
και
είναι διαδοχικοί.
Μπορείτε να μου βοηθήσετε και να το διορθώσετε παρακαλώ;
Αν πάλι θέλεις μικρό συμπλήρωμα στην γραφή, τότε λέμε ότι το αποδεικτέο γράφεται
 .
. H ισότητα είναι τώρα φανερή (με χρήση και του
 ).
).- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Ανισότητα, ισχυεί η όχι;
Δεν βλέπω πως προκύπτει αυτό. Ίσως να έχεις κάποια τυπογραφικά ή/και να έκανες κάποιες ενδιάμεσες πράξεις. (Μάλλον τοDatis-Kalali έγραψε: Αρκεί να δείξουμε ότι
 έπρεπε να είναι
έπρεπε να είναι  .) Εγώ βλέπω ότι αρκεί να δείξουμε ότι:
.) Εγώ βλέπω ότι αρκεί να δείξουμε ότι:
Το συγκεκριμένο είναι επίσης φανερό αφού:
 και
και  .
.ΥΓ: Θα μεταφέρω σύντομα το θέμα στην συζήτηση της JBMO.
-
Datis-Kalali
- Δημοσιεύσεις: 117
- Εγγραφή: Δευ Δεκ 12, 2016 5:33 pm
- Τοποθεσία: Λευκωσία
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες
