
∫ ολοκληρωτικού λογισμού
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: ∫ ολοκληρωτικού λογισμού




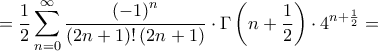





όπου χρησιμοποιήθηκαν οι τύποι
 (μετασχηματισμός Laplace) και
(μετασχηματισμός Laplace) και  http://mathworld.wolfram.com/GammaFunction.html (σχέση 50)
http://mathworld.wolfram.com/GammaFunction.html (σχέση 50)Πρώτη εναλλακτική συνέχεια :


χμ .. δεν βλέπω πως μπορεί να υπολογιστεί συμβατικά το τελευταίο ολοκλήρωμα.
Δεύτερη εναλλακτική συνέχεια, με υπεργεωμετρικές συναρτήσεις:
Η υπεργεωμετρική συνάρτηση ορίζεται ως

και αποτελεί λύση κάποιας μορφής υπεργεωμετρικής Διαφορικής εξίσωσης (δεν είναι του παρόντος).
Ο συμβολισμός
 είναι το σύμβολο του Pochhammer
είναι το σύμβολο του Pochhammer Τότε


και τελικά


Παρεμπιπτόντως

Δεν μπορώ να βρω πως μπορούμε να φτάσουμε σε περισσότερο συμβατικό αποτέλεσμα (αν υπάρχει βέβαια).
Σεραφείμ Τσιπέλης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 27 επισκέπτες
