Datis-Kalali έγραψε:1)Έχουμε

θέσεις

και

(

) με πεπεράσμενο πλήθο κάρτες. Σε κάθε βήμα μπορούμε να κάνουμε ένα απο τα εξής βήματα:
i. Αν στην θέση

έχουμε τουλάχιστον 3 κάρτες, τότε μπορούμε να πάρουμε 3 κάτρες απο αυτή την θέση και να προσθέτουμε μία κάρτα σε κάθε απο της θέσεις

,

και

. (Θεωρούμε

και

)
ii. Αν στην θέση

έχουμε τουλάχιστον

κάρτες, τότε μπορούμε να πάρουμε

κάτρες απο αυτή την θέση και να προσθέτουμε μία κάρτα σε κάθε απο της

θέσεις

,

,...,

.
Να δείξετε ότι αν έχουμε τουλάχιστον

κάρτες συνολίκα, τότε μέτα απο ένα πεπερασμένο πλήθο βήματων, μπορούμε να να έχουμε τουλάχιστον

σε κάθε θέση.
(Πήγη: Περσική ιστοσελίδα μαθηματικών)
Αρχικά επαναλαμβάνουμε το βήμα (i) για όσα περισσότερα βήματα μπορούμε. Αυτή η διαδικασία θα τελειώσει επειδή το άθροισμα των καρτών στα

μειώνεται κάθε φορά που εκτελούμε το βήμα (i).
Μπορούμε λοιπόν να καταλήξουμε σε μια κατάσταση όπου σε κάθε θέση

θα έχουμε από

μέχρι

κάρτες. Τώρα επαναλαμβάνουμε το βήμα (ii) μέχρις ούτω να συμβεί ένα από τα πιο κάτω
(α) Σε κάθε θέση

υπάρχουν τουλάχιστον

κάρτες.
(β) Δεν μπορούμε πλέον να επαναλάβουμε το βήμα (ii) επειδή δεν υπάρχουν αρκετές κάρτες στην θέση

.
Ισχυρίζομαι ότι αυτό που θα συμβεί είναι το (α), πιθανώς ταυτόχρονα με το (β). Πράγματι αν δεν συμβεί το (α), τότε θα υπάρχει

ώστε σε κάθε θέση

να έχω από

μέχρι

κάρτες, ενώ στην θέση

να έχω το πολύ

κάρτες. Τότε όμως συνολικά θα είχα το πολύ

κάρτες, άτοπο.
Είμαι τώρα σε μια κατάσταση όπου
(Α) Κάθε θέση

έχει από

έως

κάρτες.
(Β) Υπάρχει τουλάχιστον μια θέση

με ακριβώς

κάρτες.
Βρίσκω τώρα, αν υπάρχει, ακολουθία θέσεων

ώστε
(1) Στα

υπάρχουν από

κάρτες.
(2) Στα

υπάρχουν από τουλάχιστον

κάρτες.
(3) Δεν υπάρχουν

κάρτες ούτε στο

ούτε στο

.
Τότε εκτελώ το βήμα (i) διαδοχικά στις θέσεις

. Τότε στις θέσεις

θα μειωθεί το πλήθος των καρτών κατά

, στις θέσεις

θα μειωθεί το πλήθος των καρτών κατά

, και στις θέσεις

θα αυξηθεί το πλήθος των καρτών κατά

. Άρα πάλι θα είμαστε σε μια κατάσταση όπου τα (Α) και (Β) ισχύουν. [Πρέπει να ελέγξουμε τι συμβαίνει αν

διότι τότε το πλήθος των καρτών σε αυτήν την θέση θα αυξηθεί κατά

. Αλλά σε αυτήν την περίπτωση αυτή η θέση θα είχε αρχικά

κάρτες λόγω του (Β).
Επειδή όποτε εκτελώ το πιο πάνω, το πλήθος των καρτών στις θέσεις

μειώνεται, εν τέλει θα καταλήξω σε μια κατάσταση όπου ισχύουν τα (Α) και (Β) αλλά δεν υπάρχει ακολουθία θέσεων

ώστε να ισχύουν τα (1),(2),(3).
Αυτό σημαίνει ότι το πλήθος των θέσεων με

κάρτες είναι μεγαλύτερο ή ίσο από το πλήθος των θέσεων με

κάρτες. Αυτό ισχύει διότι κάθε φορά που έχω μια θέση με

κάρτες, η αμέσως επόμενη θέση που δεν έχει

κάρτες θα πρέπει να έχει

κάρτες. (Χρησιμοποιούμε επίσης ότι υπάρχει τουλάχιστον μια θέση με

κάρτες.)
Άρα το συνολικό πλήθος καρτών στις θέσεις

είναι το πολύ

. Αλλά τότε στην θέση

υπάρχουν τουλάχιστον

κάρτες. Άρα το ζητούμενο αποδείχθηκε.
 θέσεις
θέσεις  και
και  (
( ) με πεπεράσμενο πλήθο κάρτες. Σε κάθε βήμα μπορούμε να κάνουμε ένα απο τα εξής βήματα:
) με πεπεράσμενο πλήθο κάρτες. Σε κάθε βήμα μπορούμε να κάνουμε ένα απο τα εξής βήματα: έχουμε τουλάχιστον 3 κάρτες, τότε μπορούμε να πάρουμε 3 κάτρες απο αυτή την θέση και να προσθέτουμε μία κάρτα σε κάθε απο της θέσεις
έχουμε τουλάχιστον 3 κάρτες, τότε μπορούμε να πάρουμε 3 κάτρες απο αυτή την θέση και να προσθέτουμε μία κάρτα σε κάθε απο της θέσεις  ,
,  και
και  . (Θεωρούμε
. (Θεωρούμε  και
και  )
) έχουμε τουλάχιστον
έχουμε τουλάχιστον  κάρτες, τότε μπορούμε να πάρουμε
κάρτες, τότε μπορούμε να πάρουμε  κάτρες απο αυτή την θέση και να προσθέτουμε μία κάρτα σε κάθε απο της
κάτρες απο αυτή την θέση και να προσθέτουμε μία κάρτα σε κάθε απο της  θέσεις
θέσεις  ,
,  ,...,
,...,  .
.  κάρτες συνολίκα, τότε μέτα απο ένα πεπερασμένο πλήθο βήματων, μπορούμε να να έχουμε τουλάχιστον
κάρτες συνολίκα, τότε μέτα απο ένα πεπερασμένο πλήθο βήματων, μπορούμε να να έχουμε τουλάχιστον  σε κάθε θέση.
σε κάθε θέση.  , έτσι ώστε:
, έτσι ώστε:

 μειώνεται κάθε φορά που εκτελούμε το βήμα (i).
μειώνεται κάθε φορά που εκτελούμε το βήμα (i). μέχρι
μέχρι  κάρτες. Τώρα επαναλαμβάνουμε το βήμα (ii) μέχρις ούτω να συμβεί ένα από τα πιο κάτω
κάρτες. Τώρα επαναλαμβάνουμε το βήμα (ii) μέχρις ούτω να συμβεί ένα από τα πιο κάτω ώστε σε κάθε θέση
ώστε σε κάθε θέση  μέχρι
μέχρι  κάρτες, ενώ στην θέση
κάρτες, ενώ στην θέση  κάρτες. Τότε όμως συνολικά θα είχα το πολύ
κάρτες. Τότε όμως συνολικά θα είχα το πολύ
 κάρτες.
κάρτες. ώστε
ώστε υπάρχουν από
υπάρχουν από  υπάρχουν από τουλάχιστον
υπάρχουν από τουλάχιστον  κάρτες.
κάρτες. .
.  θα μειωθεί το πλήθος των καρτών κατά
θα μειωθεί το πλήθος των καρτών κατά  , και στις θέσεις
, και στις θέσεις  θα αυξηθεί το πλήθος των καρτών κατά
θα αυξηθεί το πλήθος των καρτών κατά  διότι τότε το πλήθος των καρτών σε αυτήν την θέση θα αυξηθεί κατά
διότι τότε το πλήθος των καρτών σε αυτήν την θέση θα αυξηθεί κατά  . Αλλά τότε στην θέση
. Αλλά τότε στην θέση  στον υπολογιστή σου που είναι κάπως πιο δύσκολο στο ξεκίνημα. Από εκείνον τον σύνδεσμο αγνόησε οτιδήποτε μιλάει για packages και \usepackage. Πολλά από αυτά τα «πακέτα» είναι ήδη φορτωμένα στο
στον υπολογιστή σου που είναι κάπως πιο δύσκολο στο ξεκίνημα. Από εκείνον τον σύνδεσμο αγνόησε οτιδήποτε μιλάει για packages και \usepackage. Πολλά από αυτά τα «πακέτα» είναι ήδη φορτωμένα στο  που θέλουμε είναι με την χρήση του EqEditor. Αυτός εμφανίζεται (σε ξεχωριστό παράθυρο) όταν πατάμε το κουμπί EqEditor που βρίσκεται στην μπάρα του παραθύρου δημοσίευσης.
που θέλουμε είναι με την χρήση του EqEditor. Αυτός εμφανίζεται (σε ξεχωριστό παράθυρο) όταν πατάμε το κουμπί EqEditor που βρίσκεται στην μπάρα του παραθύρου δημοσίευσης.

![1000\alpha+100\beta+10\gamma +\delta=\left ( 10\alpha +\gamma +1 \right )\cdot \left ( 10\beta +\delta+1)
\Leftrightarrow
10\alpha \cdot \left [ 99-\left ( 10\beta +\delta \right ) \right ]+10\beta \cdot (9-\gamma )+\gamma\cdot \left ( 9-\delta \right )= 1 1000\alpha+100\beta+10\gamma +\delta=\left ( 10\alpha +\gamma +1 \right )\cdot \left ( 10\beta +\delta+1)
\Leftrightarrow
10\alpha \cdot \left [ 99-\left ( 10\beta +\delta \right ) \right ]+10\beta \cdot (9-\gamma )+\gamma\cdot \left ( 9-\delta \right )= 1](/forum/ext/geomar/texintegr/latexrender/pictures/79dc661cbaa006c6d80dc57112b54acd.png)
![\displaystyle 10\alpha\left [ 99-\left ( 10\beta +\delta \right ) \right ]+10\beta (9-\gamma ) \displaystyle 10\alpha\left [ 99-\left ( 10\beta +\delta \right ) \right ]+10\beta (9-\gamma )](/forum/ext/geomar/texintegr/latexrender/pictures/3da70c728cf821bf7c98a7e567478c0b.png)
 και μη αρνητικό. Το
και μη αρνητικό. Το  είναι μη αρνητικό.
είναι μη αρνητικό.![\displaystyle 10\alpha\left [ 99-\left ( 10\beta +\delta \right ) \right ]+10\beta (9-\gamma ) = 0 \displaystyle 10\alpha\left [ 99-\left ( 10\beta +\delta \right ) \right ]+10\beta (9-\gamma ) = 0](/forum/ext/geomar/texintegr/latexrender/pictures/f0a0f7111beb090e8129d6a362876195.png)

 από την δεύτερη ισότητα, και μετά
από την δεύτερη ισότητα, και μετά  από την πρώτη.
από την πρώτη.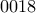 . Το κατά πόσο είναι επιτρεπτή ή όχι εξαρτάται και από την εκφώνηση. Εφόσον μιλάει για τετραψήφιους, κανονικά πρέπει να την απορρίψουμε.
. Το κατά πόσο είναι επιτρεπτή ή όχι εξαρτάται και από την εκφώνηση. Εφόσον μιλάει για τετραψήφιους, κανονικά πρέπει να την απορρίψουμε.