 , ώστε ο αριθμός:
, ώστε ο αριθμός: να διαιρείται με το
να διαιρείται με το  .
.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 , ώστε ο αριθμός:
, ώστε ο αριθμός: να διαιρείται με το
να διαιρείται με το  .
.Για να κλείνει.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Σάβ Σεπ 30, 2017 9:45 pmΑΣΚΗΣΗ 1368: Να εξετάσετε αν υπάρχει φυσικός αριθμός, ώστε ο αριθμός:
να διαιρείται με το
.
 τότε θα διαιρείται και με το
τότε θα διαιρείται και με το  . Γράφοντας διαδοχικά
. Γράφοντας διαδοχικά  , θα διαπιστώνουμε ότι ο
, θα διαπιστώνουμε ότι ο  είναι αντίστοιχα της μορφής
είναι αντίστοιχα της μορφής  (άμεσο με πράξεις). To μόνο πολλαπλάσιο του
(άμεσο με πράξεις). To μόνο πολλαπλάσιο του  προέρχεται από τον
προέρχεται από τον  , οπότε επικεντρωνόμαστε σε αυτόν.
, οπότε επικεντρωνόμαστε σε αυτόν.  έχουμε
έχουμε 
 .
. δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  .
.

Ευκολάκι!ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Κυρ Νοέμ 19, 2017 5:13 pmΑΣΚΗΣΗ 1369 Να λυθεί το σύστημα:
(Η άσκηση είναι από παλιό μαθηματικό διαγωνισμό ξένου Κράτους)

















 , ώστε ο αριθμός:
, ώστε ο αριθμός: , να είναι ρητός.
, να είναι ρητός. δεν είναι διαιρέτες του
δεν είναι διαιρέτες του  ;
; , του οποίου η βάση είναι
, του οποίου η βάση είναι  , οι δύο ίσες πλευρές
, οι δύο ίσες πλευρές  , και το ύψος
, και το ύψος  από την κορυφή
από την κορυφή  .
. , να υπολογίσετε τις γωνίες του τριγώνου.
, να υπολογίσετε τις γωνίες του τριγώνου. ικανοποιούν την
ικανοποιούν την ,
, .
.Τετραγωνίζοντας τη δοθείσα , παίρνουμε :Ορέστης Λιγνός έγραψε: ↑Κυρ Ιαν 14, 2018 2:24 pmΑΣΚΗΣΗ 1372
Θεωρούμε ισοσκελές τρίγωνο, του οποίου η βάση είναι
, οι δύο ίσες πλευρές
, και το ύψος
από την κορυφή
.
Αν, να υπολογίσετε τις γωνίες του τριγώνου.
 (*)
(*) το ύψος προς την
το ύψος προς την  . Φυσικά είναι :
. Φυσικά είναι :  . Έτσι
. Έτσι . Αλλά ( βλέπε τρίγωνο
. Αλλά ( βλέπε τρίγωνο 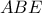 ) είναι :
) είναι :  , τελικά
, τελικά  ,
, να είναι ορθή και οι άλλες
να είναι ορθή και οι άλλες 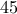 -άρες
-άρεςΟρέστη καλησπέραΟρέστης Λιγνός έγραψε: ↑Κυρ Ιαν 14, 2018 2:38 pmΑΣΚΗΣΗ 1373
Αν οιικανοποιούν την
,
να δείξετε ότι
.
 προκύπτει
προκύπτει




 προκύπτει το ζητούμενο. Για να μην γράψω όλες τις πράξεις παρατηρώ ότι
προκύπτει το ζητούμενο. Για να μην γράψω όλες τις πράξεις παρατηρώ ότι
Γεια σου Ορέστη.Ορέστης Λιγνός έγραψε: ↑Κυρ Ιαν 14, 2018 2:21 pmΑΣΚΗΣΗ 1371
Πόσοι διαιρέτες του αριθμούδεν είναι διαιρέτες του
;
 και
και 
 που δεν είναι διαιρέτες του
που δεν είναι διαιρέτες του  , θα πρέπει να έχουν μία από τις πιο κάτω μορφές:
, θα πρέπει να έχουν μία από τις πιο κάτω μορφές: , με
, με 
 , με
, με 
 , με
, με 
 , με
, με 
 , με
, με 


ΣΗΜ: Διόρθωσα στην τελευταία ομάδα διαιρετών , αντίΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Δευ Ιαν 15, 2018 1:19 pmΓεια σου Ορέστη.Ορέστης Λιγνός έγραψε: ↑Κυρ Ιαν 14, 2018 2:21 pmΑΣΚΗΣΗ 1371
Πόσοι διαιρέτες του αριθμούδεν είναι διαιρέτες του
;
και
Οι διαιρέτες τουπου δεν είναι διαιρέτες του
, θα πρέπει να έχουν μία από τις πιο κάτω μορφές:
, με
, με
, με
, με
, με
Συνεπώς το ζητούμενο πλήθος είναι
 , θέλει
, θέλει 
Ας δούμε και μια διαφορετική λύση με Τριγωνομετρία. Χρησιμοποιώ το σχήμα του Θανάση.Ορέστης Λιγνός έγραψε: ↑Κυρ Ιαν 14, 2018 2:24 pmΑΣΚΗΣΗ 1372
Θεωρούμε ισοσκελές τρίγωνο, του οποίου η βάση είναι
, οι δύο ίσες πλευρές
, και το ύψος
από την κορυφή
.
Αν, να υπολογίσετε τις γωνίες του τριγώνου.
 , με
, με  .
.
 ,
, .
.Πολλαπλασιάζω τη δοθείσα μεΟρέστης Λιγνός έγραψε: ↑Κυρ Ιαν 14, 2018 2:38 pmΑΣΚΗΣΗ 1373
Αν οιικανοποιούν την
,
να δείξετε ότι
.
 , τότε
, τότε  .
.  .
.

 που επαληθεύουν την εξίσωση
που επαληθεύουν την εξίσωση  .
. και
και  .
.  και
και 
 και
και  είναι
είναι  ή
ή  και
και  ή
ή 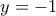 .
.
Θα δείξουμε ότιΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Τετ Ιαν 17, 2018 7:16 pmΑΣΚΗΣΗ 1374: Έστω
Να αποδείξετε ότι
ΠΗΓΗ: (Ρουμάνικο βιβλίο για διαγωνισμούς)
 .
.
 (η ισότητα ισχύει όταν
(η ισότητα ισχύει όταν  ).
). να αποδειχθεί ότι
να αποδειχθεί ότι
Αρκεί
 .
. και τα κυκλικά.
και τα κυκλικά. .
. . Προσθέτοντας τις κυκλικές μ'αυτήν έχουμε τη ζητούμενη.
. Προσθέτοντας τις κυκλικές μ'αυτήν έχουμε τη ζητούμενη.Ωραία η λύση του Ορέστη!Ορέστης Λιγνός έγραψε: ↑Τρί Μαρ 12, 2019 11:46 pmΑρκεί.
Όμως,και τα κυκλικά.
Οπότε αρκεί.
Από AM-GM, είναι. Προσθέτοντας τις κυκλικές μ'αυτήν έχουμε τη ζητούμενη.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης