
διαφορετικοί ανά δύο ακέραιοι.
Θέτουμε

Δείξτε ότι για

το πολυώνυμο είναι ανάγωγο στους ακεραίους.
Συντονιστής: Demetres



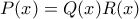 με
με ![Q, R \in \mathbb{Z}[x] Q, R \in \mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/24b8cac34c4587e353413984861e3e11.png) πολυώνυμα βαθμού μικρότερου του
πολυώνυμα βαθμού μικρότερου του  .
.  για κάθε
για κάθε 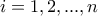 . Αφού το πολυώνυμο
. Αφού το πολυώνυμο  μηδενίζεται σε
μηδενίζεται σε  σημεία και δεν έχει βαθμό μεγαλύτερο ή ίσο του
σημεία και δεν έχει βαθμό μεγαλύτερο ή ίσο του  , είναι το μηδενικό. Έτσι τα δύο πολυώνυμα ταυτίζονται και έχουμε
, είναι το μηδενικό. Έτσι τα δύο πολυώνυμα ταυτίζονται και έχουμε  .
. και
και  . Αφού
. Αφού  , ισχύει ότι
, ισχύει ότι  οπότε
οπότε  και έχουμε άτοπο.
και έχουμε άτοπο.Αφού ταΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Νοέμ 01, 2017 1:52 pmΕίναι και τα(εννοείται ότι είναι εύκολα αλλά ξεχάστηκαν)
 ταυτίζονται, το
ταυτίζονται, το  πρέπει να είναι άρτιο.
πρέπει να είναι άρτιο.Έχουμε βέβαια και τις περιπτώσεις
 ,
,  .
.  λαμβάνουμε
λαμβάνουμε  ,
,  , άρα
, άρα  με
με 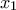 τυχόντα ακέραιο.
τυχόντα ακέραιο. λαμβάνουμε
λαμβάνουμε  ,
,  , όπου
, όπου  οι συμμετρικές παραστάσεις των
οι συμμετρικές παραστάσεις των  : λίγο δύσκολο να ισχύουν όλες αυτές οι σχέσεις ταυτόχρονα, και μάλιστα για ακεραίους, αλλά ... προς το παρόν δεν βλέπω κάποιον γρήγορο τρόπο αποκλεισμού αυτής της πιθανότητας... (Για
: λίγο δύσκολο να ισχύουν όλες αυτές οι σχέσεις ταυτόχρονα, και μάλιστα για ακεραίους, αλλά ... προς το παρόν δεν βλέπω κάποιον γρήγορο τρόπο αποκλεισμού αυτής της πιθανότητας... (Για  , για παράδειγμα, οι σχέσεις ισχύουν ... αλλά οι
, για παράδειγμα, οι σχέσεις ισχύουν ... αλλά οι  δεν είναι ακέραιοι.)
δεν είναι ακέραιοι.) η αναγωγή δεν χρειάζεται να είναι στη μορφή
η αναγωγή δεν χρειάζεται να είναι στη μορφή  . Αρκεί η μορφή
. Αρκεί η μορφή  . Έτσι, για παράδειγμα, έχουμε
. Έτσι, για παράδειγμα, έχουμε
Πολύ σωστά, και αυτό λύνει το πρόβλημα πλήρως, καθώς αρκεί να παραγοντοποιείται σε γινόμενο πρωτοβάθμιων όρων (και να έχει ακέραιες ρίζες) το πολυώνυμο

 και
και  για ακέραιους
για ακέραιους  άρα
άρα  με μόνες πιθανές λύσεις τις
με μόνες πιθανές λύσεις τις  . Σε όλες τις περιπτώσεις καταλήγουμε στην εξίσωση
. Σε όλες τις περιπτώσεις καταλήγουμε στην εξίσωση  , η γενική λύση της οποίας είναι
, η γενική λύση της οποίας είναι
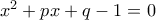 και
και 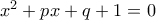 είναι τώρα είτε της μορφής
είναι τώρα είτε της μορφής  και
και  (περίπτωση
(περίπτωση  ) είτε της μορφής
) είτε της μορφής  και
και  (περίπτωση
(περίπτωση  ). Οι αντίστοιχες ταυτότητες είναι
). Οι αντίστοιχες ταυτότητες είναι 
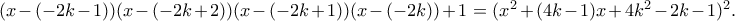
 είναι μη ανάγωγο στους ακέραιους (ακριβέστερα τετράγωνο τριωνύμου χωρίς ακέραιες ρίζες*) αν και μόνον αν οι
είναι μη ανάγωγο στους ακέραιους (ακριβέστερα τετράγωνο τριωνύμου χωρίς ακέραιες ρίζες*) αν και μόνον αν οι  είναι διαδοχικοί ακέραιοι. (Και ως απλό πόρισμα λαμβάνουμε ένα γνωστό και βεβαίως πολύ ευκολότερο αποτέλεσμα: το γινόμενο τεσσάρων διαδοχικών ακεραίων συν ένα είναι τέλειο τετράγωνο (του γινομένου του πρώτου επί τον τελευταίο συν ένα).)
είναι διαδοχικοί ακέραιοι. (Και ως απλό πόρισμα λαμβάνουμε ένα γνωστό και βεβαίως πολύ ευκολότερο αποτέλεσμα: το γινόμενο τεσσάρων διαδοχικών ακεραίων συν ένα είναι τέλειο τετράγωνο (του γινομένου του πρώτου επί τον τελευταίο συν ένα).) ισούται προς
ισούται προς 
Για μία πραλλαγή της λύσης βλέπε την Άσκηση 3 εδώ.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Νοέμ 01, 2017 12:11 amΕστω
διαφορετικοί ανά δύο ακέραιοι.
Θέτουμε
Δείξτε ότι για
το πολυώνυμο είναι ανάγωγο στους ακεραίους.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες