Πρόβλημα 1
Δύο φίλοι, οι
 και
και  , έχουν από μια υπολογιστική μηχανή και αρχίζουν να κάνουν πράξεις ταυτόχρονα. Ο
, έχουν από μια υπολογιστική μηχανή και αρχίζουν να κάνουν πράξεις ταυτόχρονα. Ο  ξεκινά με τον αριθμό
ξεκινά με τον αριθμό  και σε κάθε βήμα προσθέτει
και σε κάθε βήμα προσθέτει  , ενώ ο
, ενώ ο  ξεκινά με τον αριθμό
ξεκινά με τον αριθμό 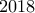 και σε κάθε βήμα αφαιρεί
και σε κάθε βήμα αφαιρεί  . Ύστερα από
. Ύστερα από  βήματα, οι δύο φίλοι καταλήγουν στο ίδιο αποτέλεσμα.
βήματα, οι δύο φίλοι καταλήγουν στο ίδιο αποτέλεσμα.(α) Να βρείτε την τιμή του
 .
.(β) Ποιο είναι το κοινό αποτέλεσμα στο οποίο καταλήγουν οι δύο φίλοι;
Πρόβλημα 2
Στο πιο κάτω σχήμα δίνεται τρίγωνο
 . Το
. Το  είναι ύψος του τριγώνου
είναι ύψος του τριγώνου  , το
, το  είναι το μέσο του
είναι το μέσο του  και το
και το  είναι σημείο του
είναι σημείο του  , ώστε το μήκος του
, ώστε το μήκος του  να είναι διπλάσιο από το μήκος του
να είναι διπλάσιο από το μήκος του  . Αν το εμβαδόν του τριγώνου
. Αν το εμβαδόν του τριγώνου  είναι
είναι  και το εμβαδόν του τετραπλεύρου
και το εμβαδόν του τετραπλεύρου  είναι
είναι  , να υπολογίσετε το εμβαδόν του τριγώνου
, να υπολογίσετε το εμβαδόν του τριγώνου  .
.Πρόβλημα 3
Τρία δοχεία, τα
 και
και  , περιέχουν διάλυμα νερού με οξύ. Το δοχείο
, περιέχουν διάλυμα νερού με οξύ. Το δοχείο  περιέχει
περιέχει  διάλυμα με περιεκτικότητα
διάλυμα με περιεκτικότητα  σε οξύ. Το δοχείο
σε οξύ. Το δοχείο  περιέχει
περιέχει  διάλυμα με περιεκτικότητα
διάλυμα με περιεκτικότητα  σε οξύ. Το δοχείο
σε οξύ. Το δοχείο  περιέχει
περιέχει  διάλυμα με άγνωστη περιεκτικότητα σε οξύ. Αδειάζουμε όλη την ποσότητα διαλύματος του δοχείου
διάλυμα με άγνωστη περιεκτικότητα σε οξύ. Αδειάζουμε όλη την ποσότητα διαλύματος του δοχείου  στα δύο πρώτα δοχεία, ώστε και τα δύο να έχουν τώρα διάλυμα με περιεκτικότητα
στα δύο πρώτα δοχεία, ώστε και τα δύο να έχουν τώρα διάλυμα με περιεκτικότητα  σε οξύ το καθένα. Να υπολογίσετε την ποσότητα (σε
σε οξύ το καθένα. Να υπολογίσετε την ποσότητα (σε  ) από διάλυμα που προσθέσαμε στο δοχείο
) από διάλυμα που προσθέσαμε στο δοχείο  .
.Πρόβλημα 4
Να βρείτε όλους τους φυσικούς αριθμούς που είναι μικρότεροι του
 και οι οποίοι όταν διαιρεθούν με τους αριθμούς
και οι οποίοι όταν διαιρεθούν με τους αριθμούς  και
και  αφήνουν υπόλοιπα
αφήνουν υπόλοιπα  και
και  , αντίστοιχα.
, αντίστοιχα.
 και στο πρώτο βήμα προσθέτει
και στο πρώτο βήμα προσθέτει  , στο δεύτερο βήμα
, στο δεύτερο βήμα  , στο τρίτο βήμα
, στο τρίτο βήμα  . Με πόσους διαφορετικούς τρόπους μπορεί ο Γιώργος να ξεπληρώσει το χρέος του, χρησιμοποιώντας κέρματα του €
. Με πόσους διαφορετικούς τρόπους μπορεί ο Γιώργος να ξεπληρώσει το χρέος του, χρησιμοποιώντας κέρματα του € και €
και € ;
; κέρματα του €
κέρματα του € ισχύει ότι:
ισχύει ότι: 
 θετικοί πραγματικοί αριθμοί, για τους οποίους ισχύει ότι
θετικοί πραγματικοί αριθμοί, για τους οποίους ισχύει ότι  .
. .
. είναι ακέραιος αριθμός.
είναι ακέραιος αριθμός. τέτοιοι, ώστε ο αριθμός
τέτοιοι, ώστε ο αριθμός  να είναι ακέραιος και να ισχύει ότι:
να είναι ακέραιος και να ισχύει ότι: 
 είναι τετράγωνο πλευράς
είναι τετράγωνο πλευράς  και το
και το  είναι τόξο με κέντρο το
είναι τόξο με κέντρο το 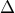 και ακτίνα
και ακτίνα  και ακτίνα
και ακτίνα  εφάπτεται στις πλευρές
εφάπτεται στις πλευρές  και στο τόξο
και στο τόξο  .
.
 ακέραιοι αριθμοί, για τους οποίους ισχύει ότι
ακέραιοι αριθμοί, για τους οποίους ισχύει ότι  .
. είναι τέλειο τετράγωνο ακέραιου αριθμού.
είναι τέλειο τετράγωνο ακέραιου αριθμού. οπότε έχουμε διαδοχικά
οπότε έχουμε διαδοχικά








 οπότε
οπότε  .
. τέτοιους ώστε
τέτοιους ώστε  οπότε και θα ισχύει
οπότε και θα ισχύει  .
. 




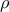 η ακτίνα του κύκλου. Με Πυθαγόρειο βρίσκω ότι
η ακτίνα του κύκλου. Με Πυθαγόρειο βρίσκω ότι  και
και 



 το ζητούμενο εμβαδόν,
το ζητούμενο εμβαδόν,  το εμβαδόν του τεταρτοκυκλίου και
το εμβαδόν του τεταρτοκυκλίου και  το εμβαδόν του κύκλου.
το εμβαδόν του κύκλου.

 είναι διπλάσιο από το μήκος του
είναι διπλάσιο από το μήκος του  , το
, το
 . Γνωρίζουμε ότι
. Γνωρίζουμε ότι  είναι το μέσο του
είναι το μέσο του  επομένως
επομένως 




