Τσιαλας Νικολαος έγραψε: ↑Σάβ Μαρ 03, 2018 2:47 pmΠρόβλημα 1.
Να εξετάσετε αν υπάρχει πραγματικός αριθμός, τέτοιος ώστε οι αριθμοί
και
να είναι και οι δύο ρητοί όπου
.
Πρόβλημα 3.
Θεωρούμε τους θετικούς ακεραίουςέτσι ώστε ο αριθμός
, όπου
να είναι ακέραιος. Αν
είναι περιττός, να βρεθούν οι ακέραιοι
. Αν ο
άρτιος μπορούμε;
Θέματα μεγάλων
Πρόβλημα 1.
Να λυθεί η εξίσωσηπου προκύπτει.
Πρόβλημα 4.
α) Βρείτε ένα κάτω φράγμα για το.
β) Το πλήθος των τριγώνων εμβαδού 1 με κορυφές απόσημεία (όχι αναγκαστικά μη συνευθειακά) είναι μικρότερο από
.
ΑΡΧΙΜΗΔΗΣ 2017-2018
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Για να δούμε και κάποια ερωτήματα bonus.
Σιλουανός Μπραζιτίκος
Λέξεις Κλειδιά:
- S.E.Louridas
- Δημοσιεύσεις: 5954
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Καλημέρα.
Άλλος ένας διαγωνισμός «Αρχιμήδης» τελείωσε. Τέτοιοι διαγωνισμοί ως υψηλοί θεσμοί ανίχνευσης ταλέντων, δεν θα πρέπει με τίποτα να προσφέρονται για να επενδύουμε κοινωνικά, δεν πρόκειται με τίποτα για αυτό. Μέγας ουσιαστικός επιτυχών σε ένα τέτοιο διαγωνισμό είναι κάθε διαγωνιζόμενος σε αυτόν και λόγω του οδοιπορικού του μέχρι εκεί. Η συμμετοχή στον «Αρχιμήδη» είναι κορυφαίο γεγονός και αποτελεί από μόνη της την απόδειξη ότι ο συμμετέχων μετρά στον τομέα της Μαθηματικής και όχι μόνο απόδοσης. Έχω δει τεράστιες Μαθηματικές οντότητες που έφτασαν μέχρι τον «Αρχιμήδη» και για κάποιον λόγο δεν συνέχισαν και όμως αυτή τη στιγμή ως Μαθηματικοί ή θετικοί επιστήμονες μεσουρανούν. Τέτοιοι διαγωνισμοί εκτός των άλλων διδάσκουν με έμφαση την συνέχιση της μάχης με πείσμα, και με τίποτα δεν διδάσκουν τη παραίτηση σε πιθανή πρόσκαιρη αποτυχία. Προφανώς και αξίζουν σεβασμό και θαυμασμό οι συμμετέχοντες στον «Αρχιμήδη». Σίγουρα αυτοί που ξεχώρισαν στον διαγωνισμό αυτό και συνεχίζουν αξίζουν ιδιαίτερα εύσημα, αλλά και επιπλέον κίνητρα και επένδυση από την επίσημη πολιτεία, και σίγουρα όλοι μας ευχόμαστε να συνεχίσουν με Υγεία και Πρόοδο την επιστημονική αυτή πορεία τους.
Επιτρέψτε μου να εκφράσω τον θαυμασμό μου και τον σεβασμό μου για τους συμμετέχοντες στον διαγωνισμό «Αρχιμήδης». Να ευχηθώ ιδιαίτερα στους επιτυχόντες καλή συνέχεια και επιτυχία στους επόμενους διαγωνισμούς και να ξέρουν ότι οι Έλληνες συμπατριώτες παρακολουθούν την πορεία τους αυτή με αγάπη, επιπλέον θαυμασμό αλλά και σεβασμό, αφού αποτελούν για όλους φάρους ζωής.
Άλλος ένας διαγωνισμός «Αρχιμήδης» τελείωσε. Τέτοιοι διαγωνισμοί ως υψηλοί θεσμοί ανίχνευσης ταλέντων, δεν θα πρέπει με τίποτα να προσφέρονται για να επενδύουμε κοινωνικά, δεν πρόκειται με τίποτα για αυτό. Μέγας ουσιαστικός επιτυχών σε ένα τέτοιο διαγωνισμό είναι κάθε διαγωνιζόμενος σε αυτόν και λόγω του οδοιπορικού του μέχρι εκεί. Η συμμετοχή στον «Αρχιμήδη» είναι κορυφαίο γεγονός και αποτελεί από μόνη της την απόδειξη ότι ο συμμετέχων μετρά στον τομέα της Μαθηματικής και όχι μόνο απόδοσης. Έχω δει τεράστιες Μαθηματικές οντότητες που έφτασαν μέχρι τον «Αρχιμήδη» και για κάποιον λόγο δεν συνέχισαν και όμως αυτή τη στιγμή ως Μαθηματικοί ή θετικοί επιστήμονες μεσουρανούν. Τέτοιοι διαγωνισμοί εκτός των άλλων διδάσκουν με έμφαση την συνέχιση της μάχης με πείσμα, και με τίποτα δεν διδάσκουν τη παραίτηση σε πιθανή πρόσκαιρη αποτυχία. Προφανώς και αξίζουν σεβασμό και θαυμασμό οι συμμετέχοντες στον «Αρχιμήδη». Σίγουρα αυτοί που ξεχώρισαν στον διαγωνισμό αυτό και συνεχίζουν αξίζουν ιδιαίτερα εύσημα, αλλά και επιπλέον κίνητρα και επένδυση από την επίσημη πολιτεία, και σίγουρα όλοι μας ευχόμαστε να συνεχίσουν με Υγεία και Πρόοδο την επιστημονική αυτή πορεία τους.
Επιτρέψτε μου να εκφράσω τον θαυμασμό μου και τον σεβασμό μου για τους συμμετέχοντες στον διαγωνισμό «Αρχιμήδης». Να ευχηθώ ιδιαίτερα στους επιτυχόντες καλή συνέχεια και επιτυχία στους επόμενους διαγωνισμούς και να ξέρουν ότι οι Έλληνες συμπατριώτες παρακολουθούν την πορεία τους αυτή με αγάπη, επιπλέον θαυμασμό αλλά και σεβασμό, αφού αποτελούν για όλους φάρους ζωής.
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
Γιάννης Μπόρμπας
- Δημοσιεύσεις: 217
- Εγγραφή: Τρί Δεκ 13, 2016 10:41 pm
- Τοποθεσία: Χανιά
Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Για τα θέματα των μεγάλων μπορείτε να δείτε και διαφορετικές (ίσως) λύσεις εδώ:
Πρόβλημα 1
Πρόβλημα 2
Πρόβλημα 3
Πρόβλημα 4
Πρόβλημα 1
Πρόβλημα 2
Πρόβλημα 3
Πρόβλημα 4
Γιάννης Μπορμπαντωνάκης
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Επανέρχομαι διότι η απόδειξη που είχα δώσει ήταν λανθασμένη.Τσιαλας Νικολαος έγραψε: ↑Σάβ Μαρ 03, 2018 2:47 pmΘέματα μικρών
Πρόβλημα 2.
Θεωρούμε τετράγωνοπλευράς
, το οποίο υποδιαιρούμε με ευθείες παράλληλες προς τις πλευρές του σε
μικρά τετράγωνα πλευράς
. Χρωματίζουμε
μικρά τετράγωνα μαύρα, ενώ όλα τα υπόλοιπα
τετράγωνα είναι λευκά. Υποθέτουμε ότι υπάρχει θετικός ακέραιος
, τέτοιος ώστε, ανεξάρτητα από την θέση των
μαύρων μικρών τετραγώνων, υπάρχει ορθογώνιο εμβαδού
με πλευρές παράλληλες στις πλευρές του
και με όλα τα μικρά τετράγωνα από τα οποία αποτελείται να είναι λευκά, που μπορεί να αποκοπεί από το τετράγωνο
. Να βρεθεί η μέγιστη δυνατή τιμή του
.
Το πιο κάτω σχήμα δείχνει ότι
 .
.![\begin{tikzpicture}[scale=0.6,line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.6,-0.56) rectangle (9.04,8.52);
\fill[line width=2.pt,fill=black,fill opacity=1.0] (2.,2.) -- (2.,1.) -- (3.,1.) -- (3.,2.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (1.,5.) -- (1.,4.) -- (2.,4.) -- (2.,5.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (2.,7.) -- (2.,6.) -- (3.,6.) -- (3.,7.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (4.,4.) -- (4.,3.) -- (5.,3.) -- (5.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,2.) -- (5.,1.) -- (6.,1.) -- (6.,2.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (6.,5.) -- (6.,4.) -- (7.,4.) -- (7.,5.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,7.) -- (5.,6.) -- (6.,6.) -- (6.,7.) -- cycle;
\draw [line width=2.pt] (0.,8.)-- (0.,0.);
\draw [line width=2.pt] (0.,0.)-- (8.,0.);
\draw [line width=2.pt] (0.,1.)-- (8.,1.);
\draw [line width=2.pt] (0.,2.)-- (8.,2.);
\draw [line width=2.pt] (8.,3.)-- (0.,3.);
\draw [line width=2.pt] (0.,4.)-- (8.,4.);
\draw [line width=2.pt] (8.,5.)-- (0.,5.);
\draw [line width=2.pt] (0.,6.)-- (8.,6.);
\draw [line width=2.pt] (8.,7.)-- (0.,7.);
\draw [line width=2.pt] (0.,8.)-- (8.,8.);
\draw [line width=2.pt] (8.,8.)-- (8.,0.);
\draw [line width=2.pt] (1.,0.)-- (1.,8.);
\draw [line width=2.pt] (2.,8.)-- (2.,0.);
\draw [line width=2.pt] (3.,0.)-- (3.,8.);
\draw [line width=2.pt] (4.,8.)-- (4.,0.);
\draw [line width=2.pt] (5.,0.)-- (5.,8.);
\draw [line width=2.pt] (6.,8.)-- (6.,0.);
\draw [line width=2.pt] (7.,0.)-- (7.,8.);
\draw [line width=2.pt] (2.,2.)-- (2.,1.);
\draw [line width=2.pt] (2.,1.)-- (3.,1.);
\draw [line width=2.pt] (3.,1.)-- (3.,2.);
\draw [line width=2.pt] (3.,2.)-- (2.,2.);
\draw [line width=2.pt] (1.,5.)-- (1.,4.);
\draw [line width=2.pt] (1.,4.)-- (2.,4.);
\draw [line width=2.pt] (2.,4.)-- (2.,5.);
\draw [line width=2.pt] (2.,5.)-- (1.,5.);
\draw [line width=2.pt] (2.,7.)-- (2.,6.);
\draw [line width=2.pt] (2.,6.)-- (3.,6.);
\draw [line width=2.pt] (3.,6.)-- (3.,7.);
\draw [line width=2.pt] (3.,7.)-- (2.,7.);
\draw [line width=2.pt] (4.,4.)-- (4.,3.);
\draw [line width=2.pt] (4.,3.)-- (5.,3.);
\draw [line width=2.pt] (5.,3.)-- (5.,4.);
\draw [line width=2.pt] (5.,4.)-- (4.,4.);
\draw [line width=2.pt] (5.,2.)-- (5.,1.);
\draw [line width=2.pt] (5.,1.)-- (6.,1.);
\draw [line width=2.pt] (6.,1.)-- (6.,2.);
\draw [line width=2.pt] (6.,2.)-- (5.,2.);
\draw [line width=2.pt] (6.,5.)-- (6.,4.);
\draw [line width=2.pt] (6.,4.)-- (7.,4.);
\draw [line width=2.pt] (7.,4.)-- (7.,5.);
\draw [line width=2.pt] (7.,5.)-- (6.,5.);
\draw [line width=2.pt] (5.,7.)-- (5.,6.);
\draw [line width=2.pt] (5.,6.)-- (6.,6.);
\draw [line width=2.pt] (6.,6.)-- (6.,7.);
\draw [line width=2.pt] (6.,7.)-- (5.,7.);
\end{tikzpicture} \begin{tikzpicture}[scale=0.6,line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.6,-0.56) rectangle (9.04,8.52);
\fill[line width=2.pt,fill=black,fill opacity=1.0] (2.,2.) -- (2.,1.) -- (3.,1.) -- (3.,2.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (1.,5.) -- (1.,4.) -- (2.,4.) -- (2.,5.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (2.,7.) -- (2.,6.) -- (3.,6.) -- (3.,7.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (4.,4.) -- (4.,3.) -- (5.,3.) -- (5.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,2.) -- (5.,1.) -- (6.,1.) -- (6.,2.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (6.,5.) -- (6.,4.) -- (7.,4.) -- (7.,5.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,7.) -- (5.,6.) -- (6.,6.) -- (6.,7.) -- cycle;
\draw [line width=2.pt] (0.,8.)-- (0.,0.);
\draw [line width=2.pt] (0.,0.)-- (8.,0.);
\draw [line width=2.pt] (0.,1.)-- (8.,1.);
\draw [line width=2.pt] (0.,2.)-- (8.,2.);
\draw [line width=2.pt] (8.,3.)-- (0.,3.);
\draw [line width=2.pt] (0.,4.)-- (8.,4.);
\draw [line width=2.pt] (8.,5.)-- (0.,5.);
\draw [line width=2.pt] (0.,6.)-- (8.,6.);
\draw [line width=2.pt] (8.,7.)-- (0.,7.);
\draw [line width=2.pt] (0.,8.)-- (8.,8.);
\draw [line width=2.pt] (8.,8.)-- (8.,0.);
\draw [line width=2.pt] (1.,0.)-- (1.,8.);
\draw [line width=2.pt] (2.,8.)-- (2.,0.);
\draw [line width=2.pt] (3.,0.)-- (3.,8.);
\draw [line width=2.pt] (4.,8.)-- (4.,0.);
\draw [line width=2.pt] (5.,0.)-- (5.,8.);
\draw [line width=2.pt] (6.,8.)-- (6.,0.);
\draw [line width=2.pt] (7.,0.)-- (7.,8.);
\draw [line width=2.pt] (2.,2.)-- (2.,1.);
\draw [line width=2.pt] (2.,1.)-- (3.,1.);
\draw [line width=2.pt] (3.,1.)-- (3.,2.);
\draw [line width=2.pt] (3.,2.)-- (2.,2.);
\draw [line width=2.pt] (1.,5.)-- (1.,4.);
\draw [line width=2.pt] (1.,4.)-- (2.,4.);
\draw [line width=2.pt] (2.,4.)-- (2.,5.);
\draw [line width=2.pt] (2.,5.)-- (1.,5.);
\draw [line width=2.pt] (2.,7.)-- (2.,6.);
\draw [line width=2.pt] (2.,6.)-- (3.,6.);
\draw [line width=2.pt] (3.,6.)-- (3.,7.);
\draw [line width=2.pt] (3.,7.)-- (2.,7.);
\draw [line width=2.pt] (4.,4.)-- (4.,3.);
\draw [line width=2.pt] (4.,3.)-- (5.,3.);
\draw [line width=2.pt] (5.,3.)-- (5.,4.);
\draw [line width=2.pt] (5.,4.)-- (4.,4.);
\draw [line width=2.pt] (5.,2.)-- (5.,1.);
\draw [line width=2.pt] (5.,1.)-- (6.,1.);
\draw [line width=2.pt] (6.,1.)-- (6.,2.);
\draw [line width=2.pt] (6.,2.)-- (5.,2.);
\draw [line width=2.pt] (6.,5.)-- (6.,4.);
\draw [line width=2.pt] (6.,4.)-- (7.,4.);
\draw [line width=2.pt] (7.,4.)-- (7.,5.);
\draw [line width=2.pt] (7.,5.)-- (6.,5.);
\draw [line width=2.pt] (5.,7.)-- (5.,6.);
\draw [line width=2.pt] (5.,6.)-- (6.,6.);
\draw [line width=2.pt] (6.,6.)-- (6.,7.);
\draw [line width=2.pt] (6.,7.)-- (5.,7.);
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/e042daf091403ba1954b0e4a486ff3f7.png)
Για να δείξουμε ότι
 , απλά παρατηρούμε ότι μία στήλη δεν θα έχει καθόλου μαύρα τετράγωνα.
, απλά παρατηρούμε ότι μία στήλη δεν θα έχει καθόλου μαύρα τετράγωνα.-
kimjonarfib
- Δημοσιεύσεις: 34
- Εγγραφή: Σάβ Ιαν 07, 2017 8:17 pm
Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Συγγνώμη μπορεί κανείς να ανεβάσει το 3 των μικρών.Αν και δεν βλέπω(εγώ τουλάχιστον) λάθη στους συλλογισμούς δεν βγάζω κάποιο καλό αποτέλεσμα.
Ευχαριστώ
Ευχαριστώ
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Επειδή οΤσιαλας Νικολαος έγραψε: ↑Σάβ Μαρ 03, 2018 2:47 pmΘέματα μικρών
Πρόβλημα 3.
Θεωρούμε τους θετικούς ακεραίουςέτσι ώστε ο αριθμός
, όπου
να είναι ακέραιος. Να αποδείξετε ότι, αν ο
είναι περιττός, τότε ο
είναι τέλειο τετράγωνο.
 είναι ακέραιος, τότε
είναι ακέραιος, τότε  . Αφού λοιπόν ο
. Αφού λοιπόν ο  είναι περιττός, τότε και ο
είναι περιττός, τότε και ο  είναι περιττός.
είναι περιττός.Γράφουμε
 όπου
όπου  ο μέγιστος κοινός διαιρέτης των
ο μέγιστος κοινός διαιρέτης των  . [Αυτό είναι κλασικό πρώτο βήμα σε τέτοιες ασκήσεις.]
. [Αυτό είναι κλασικό πρώτο βήμα σε τέτοιες ασκήσεις.]Τότε
 και
και 
Πρέπει λοιπόν
 και αφού
και αφού  περιττός, τότε
περιττός, τότε  . Έστω
. Έστω  . Τότε
. Τότε
Άρα
 . Όμως
. Όμως  και
και  , οπότε είναι
, οπότε είναι  .
. Τότε έχω
 και
και  οπότε το ζητούμενο αποδείχθηκε.
οπότε το ζητούμενο αποδείχθηκε.- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Ας ψάξουμε για κάθε τιμή του
 , να βρούμε όλες τις θετικές ακέραιες λύσεις της εξίσωσης
, να βρούμε όλες τις θετικές ακέραιες λύσεις της εξίσωσης  .
.Θα χρησιμοποιήσουμε Vieta jumping. To
 είναι ρίζα της εξίσωσης
είναι ρίζα της εξίσωσης  . Η άλλη ρίζα πρέπει να είναι η
. Η άλλη ρίζα πρέπει να είναι η  . Οπότε αν η
. Οπότε αν η  είναι λύση, το ίδιο ισχύει και για την
είναι λύση, το ίδιο ισχύει και για την  . Ομοίως, βρίσκουμε ότι
. Ομοίως, βρίσκουμε ότι  είναι λύση.
είναι λύση.Αν η
 είναι η λύση με το ελάχιστο άθροισμα
είναι η λύση με το ελάχιστο άθροισμα  αναγκαστικά πρέπει
αναγκαστικά πρέπει  και
και  . Οι δύο αυτές συνθήκες δίνουν
. Οι δύο αυτές συνθήκες δίνουν  ή
ή  .
. Αν
 , τότε
, τότε  που δίνει
που δίνει  και άρα
και άρα  ή
ή  . (Οπότε είναι και
. (Οπότε είναι και  ή
ή  αντίστοιχα.)
αντίστοιχα.)Αν
 , τότε
, τότε  . Πρέπει
. Πρέπει  το οποίο όμως είναι αδύνατο.
το οποίο όμως είναι αδύνατο.Κάθε μια από τις ελάχιστες λύσεις που βρήκαμε, προκύπτει από μια άλλη λύση μέσω Vieta jumping, και αντίστροφα.
Ξεκινώντας από την
 , βρίσκουμε τις λύσεις
, βρίσκουμε τις λύσεις 
Ισχυρίζομαι ότι όλες αυτές οι λύσεις δίνονται από τον τύπο
 και
και  όπου
όπου  είναι η ακολουθία
είναι η ακολουθία  που ορίζεται από τον αναδρομικό τύπο
που ορίζεται από τον αναδρομικό τύπο  (με
(με  ).
).Θα το δείξω επαγωγικά. Πρώτα όμως θα δείξω επαγωγικά ότι ισχύει η σχέση
 . Για
. Για  είναι άμεσο. Για το επαγωγικό βήμα παρατηρούμε ότι
είναι άμεσο. Για το επαγωγικό βήμα παρατηρούμε ότι
Για να δείξουμε τον ισχυρισμό για το ποιες είναι οι λύσεις, αν η
 είναι λύση τότε είναι και η
είναι λύση τότε είναι και η  καθώς και η
καθώς και η 
Με παρόμοιο τρόπο βρίσκουμε ότι η λύση
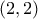 προκύπτει από τις λύσεις της μορφής
προκύπτει από τις λύσεις της μορφής  και
και  όπου
όπου  είναι η ακολουθία
είναι η ακολουθία  που ορίζεται από τον αναδρομικό τύπο
που ορίζεται από τον αναδρομικό τύπο  .
. Η λύση
 προκύπτει από τις λύσεις της μορφής
προκύπτει από τις λύσεις της μορφής  και
και  όπου
όπου  είναι η ακολουθία
είναι η ακολουθία  που ορίζεται από τον αναδρομικό τύπο
που ορίζεται από τον αναδρομικό τύπο  .
.Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Μεγαλοι 3Α
ΕΣΤΩ θα δείξουμε οτι
θα δείξουμε οτι  ομόσημα
ομόσημα 
υποθετω οτι η πρωτη διαφορά που βρίσκω ετερόσημη απο όλες τις προηγούμενες είναι η τότε
τότε
 αρα
αρα  ή
ή  ατοπο και στις 2 περιπτώσεις΄.
ατοπο και στις 2 περιπτώσεις΄.
Το πολυώνυμο παίρνει την ιδια τιμή
παίρνει την ιδια τιμή  για
για  διαφορετικες τιμες του
διαφορετικες τιμες του  τις
τις  κατα μια τουλαχιστον επιπλεον του βαθμού του
κατα μια τουλαχιστον επιπλεον του βαθμού του  αρα ειναι σταθεροό
αρα ειναι σταθεροό
Ομοια και για το
ΕΣΤΩ
 θα δείξουμε οτι
θα δείξουμε οτι  ομόσημα
ομόσημα 
υποθετω οτι η πρωτη διαφορά που βρίσκω ετερόσημη απο όλες τις προηγούμενες είναι η
 τότε
τότε αρα
αρα  ή
ή  ατοπο και στις 2 περιπτώσεις΄.
ατοπο και στις 2 περιπτώσεις΄. Το πολυώνυμο
 παίρνει την ιδια τιμή
παίρνει την ιδια τιμή  για
για  διαφορετικες τιμες του
διαφορετικες τιμες του  τις
τις  κατα μια τουλαχιστον επιπλεον του βαθμού του
κατα μια τουλαχιστον επιπλεον του βαθμού του  αρα ειναι σταθεροό
αρα ειναι σταθεροόΟμοια και για το

-
Κω.Κωνσταντινίδης
- Δημοσιεύσεις: 42
- Εγγραφή: Πέμ Μαρ 22, 2018 5:40 pm
Re: ΑΡΧΙΜΗΔΗΣ 2017-2018
Για το 3 των μικρών:
Ισοδύναμα είναι .Συνεπώς πρέπει ο
.Συνεπώς πρέπει ο  να είναι ακέραιος (και αφού α,b θετικοί ακέραιοι θα είναι και ο L επίσης θετικός). Έστω προς άτοπο ότι ο
να είναι ακέραιος (και αφού α,b θετικοί ακέραιοι θα είναι και ο L επίσης θετικός). Έστω προς άτοπο ότι ο  δεν είναι τέλειο τετράγωνο ακεραίου. Τότε υπάρχει πρώτος
δεν είναι τέλειο τετράγωνο ακεραίου. Τότε υπάρχει πρώτος  που διαιρεί τον a με
που διαιρεί τον a με  όπου m μη αρνητικός ακέραιος.
όπου m μη αρνητικός ακέραιος.
Αφού ο διαιρεί τον
διαιρεί τον  έπεται ότι
έπεται ότι  . Άρα
. Άρα  .
.
Ισχύει ότι (
(  ακέραιος). Επειδή
ακέραιος). Επειδή  και
και  και
και  προκύπτει ότι
προκύπτει ότι 

 . Τότε όμως ο a είναι άρτιος το οποίο είναι άτοπο αφού τότε ο b θα 'πρεπε να ήταν άρτιος(από την διαιρετότητα
. Τότε όμως ο a είναι άρτιος το οποίο είναι άτοπο αφού τότε ο b θα 'πρεπε να ήταν άρτιος(από την διαιρετότητα  /
/ ).
).
Άρα δεν υπάρχει πρώτος αριθμός p που διαιρεί σε περιττή δύναμη τον a και το ζητούμενο έπεται.
Σημείωση:Με συμβολίζουμε την μέγιστη δύναμη του p που διαιρεί τον x. Για παράδειγμα,για την μέγιστη δύναμη του 7 που διαιρεί το 21 γράφουμε
συμβολίζουμε την μέγιστη δύναμη του p που διαιρεί τον x. Για παράδειγμα,για την μέγιστη δύναμη του 7 που διαιρεί το 21 γράφουμε  .
.
Ισοδύναμα είναι
 .Συνεπώς πρέπει ο
.Συνεπώς πρέπει ο  να είναι ακέραιος (και αφού α,b θετικοί ακέραιοι θα είναι και ο L επίσης θετικός). Έστω προς άτοπο ότι ο
να είναι ακέραιος (και αφού α,b θετικοί ακέραιοι θα είναι και ο L επίσης θετικός). Έστω προς άτοπο ότι ο  δεν είναι τέλειο τετράγωνο ακεραίου. Τότε υπάρχει πρώτος
δεν είναι τέλειο τετράγωνο ακεραίου. Τότε υπάρχει πρώτος  που διαιρεί τον a με
που διαιρεί τον a με  όπου m μη αρνητικός ακέραιος.
όπου m μη αρνητικός ακέραιος.Αφού ο
 διαιρεί τον
διαιρεί τον  έπεται ότι
έπεται ότι  . Άρα
. Άρα  .
.Ισχύει ότι
 (
(  ακέραιος). Επειδή
ακέραιος). Επειδή  και
και  και
και  προκύπτει ότι
προκύπτει ότι 

 . Τότε όμως ο a είναι άρτιος το οποίο είναι άτοπο αφού τότε ο b θα 'πρεπε να ήταν άρτιος(από την διαιρετότητα
. Τότε όμως ο a είναι άρτιος το οποίο είναι άτοπο αφού τότε ο b θα 'πρεπε να ήταν άρτιος(από την διαιρετότητα  /
/ ).
).Άρα δεν υπάρχει πρώτος αριθμός p που διαιρεί σε περιττή δύναμη τον a και το ζητούμενο έπεται.
Σημείωση:Με
 συμβολίζουμε την μέγιστη δύναμη του p που διαιρεί τον x. Για παράδειγμα,για την μέγιστη δύναμη του 7 που διαιρεί το 21 γράφουμε
συμβολίζουμε την μέγιστη δύναμη του p που διαιρεί τον x. Για παράδειγμα,για την μέγιστη δύναμη του 7 που διαιρεί το 21 γράφουμε  .
.Κωνσταντινίδης Κωνσταντίνος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες
