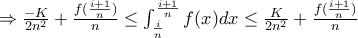Έστω
![f:[{0,1}]\longrightarrow\mathbb{R} f:[{0,1}]\longrightarrow\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/fa9401bcfae43df43f8e9fcaedb5f4f3.png) μία συνάρτηση με την ιδιότητα Lipschitz, δηλαδή τέτοια ώστε, για
μία συνάρτηση με την ιδιότητα Lipschitz, δηλαδή τέτοια ώστε, για  και για κάθε
και για κάθε ![x,\,y\in[0,1] x,\,y\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/3cb8f3cc0c592f3ee0b656c33dd81450.png) , να ισχύει:
, να ισχύει:
Να αποδειχθεί ότι, για κάθε
 , ισχύει
, ισχύει 
Σημείωση: Η άσκηση υπάρχει άλυτη σε βιβλίο Απ. Λογ. ΙΙ και είναι γενίκευση της 1ης ανισότητας (που δημοσίευσε ο Λ. Κατσάπας). Έχω λύση για την περίπτωση όπου το φράγμα είναι
 αλλά όχι και για το
αλλά όχι και για το  .
.




![\left[\frac{\kappa-1}{\nu},\frac{\kappa}{\nu}\right]\,,\; \kappa=1,2,\ldots,\nu \left[\frac{\kappa-1}{\nu},\frac{\kappa}{\nu}\right]\,,\; \kappa=1,2,\ldots,\nu](/forum/ext/geomar/texintegr/latexrender/pictures/eacb335bc9773c0fface5483743e7493.png) , από όπου
, από όπου 

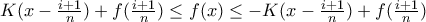
![\forall x\in [\frac{i}{n},\frac{i+1}{n}] ,\forall i\in {0,1,2,...,n-1} \forall x\in [\frac{i}{n},\frac{i+1}{n}] ,\forall i\in {0,1,2,...,n-1}](/forum/ext/geomar/texintegr/latexrender/pictures/e23fe4a9d1e14cbbd9d58b2317ff7dda.png)

![\Rightarrow \left [\frac{K(x-\frac{i+1}{n})^2}{2} +xf(\frac{i+1}{n}) \right ]_{\frac{i}{n}}^{\frac{i+1}{n}}\leq \int_{\frac{i}{n}}^{\frac{i+1}{n}}f(x)dx\leq \left [\frac{-K(x-\frac{i+1}{n})^2}{2} +xf(\frac{i+1}{n}) \right ]_{\frac{i}{n}}^{\frac{i+1}{n}} \Rightarrow \left [\frac{K(x-\frac{i+1}{n})^2}{2} +xf(\frac{i+1}{n}) \right ]_{\frac{i}{n}}^{\frac{i+1}{n}}\leq \int_{\frac{i}{n}}^{\frac{i+1}{n}}f(x)dx\leq \left [\frac{-K(x-\frac{i+1}{n})^2}{2} +xf(\frac{i+1}{n}) \right ]_{\frac{i}{n}}^{\frac{i+1}{n}}](/forum/ext/geomar/texintegr/latexrender/pictures/93507988973d3ee3083adb53db6b043e.png)