 , με τα δεδομένα του σχήματος .
, με τα δεδομένα του σχήματος .Υπολογίστε την ακτίνα κύκλου
 επίσης εφαπτόμενου των πλευρών της
επίσης εφαπτόμενου των πλευρών της  , ώστε
, ώστε το τμήμα
 της κοινής εσωτερικής εφαπτομένης των δύο κύκλων του οποίου τα άκρα
της κοινής εσωτερικής εφαπτομένης των δύο κύκλων του οποίου τα άκρα βρίσκονται στις πλευρές της
 να δημιουργεί το ισοσκελές τρίγωνο
να δημιουργεί το ισοσκελές τρίγωνο  .
.
 τα σημεία επαφής του κύκλου
τα σημεία επαφής του κύκλου  και την
και την  ανήκουν στην διχοτόμο της
ανήκουν στην διχοτόμο της  , άρα είναι συνευθειακά.
, άρα είναι συνευθειακά. είναι ισοσκελές, τα
είναι ισοσκελές, τα  είναι συνευθειακά (ανήκουν στην μεσοκάθετο της
είναι συνευθειακά (ανήκουν στην μεσοκάθετο της  ).
). .
. , και
, και 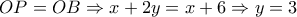 .
. .
. (1).
(1). η ημιπερίμετρος του
η ημιπερίμετρος του  (2).
(2).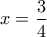 .
. .
.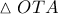 αν
αν  τότε
τότε  λόγω του Θ. διχοτόμου και άρα από το
λόγω του Θ. διχοτόμου και άρα από το  .
. και ημιπερίμετρο
και ημιπερίμετρο  .
. του παρεγγεγραμμένου κύκλου στην πλευρά
του παρεγγεγραμμένου κύκλου στην πλευρά 
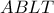 είναι ορθογώνιο, άρα
είναι ορθογώνιο, άρα  Αλλά,
Αλλά,  και με Π. Θ
και με Π. Θ  Οπότε,
Οπότε, 
