 για τις οποίες ισχύει
για τις οποίες ισχύει 
για κάθε
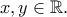
Συντονιστές: achilleas, emouroukos, silouan
 για τις οποίες ισχύει
για τις οποίες ισχύει 
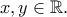
 και παίρνουμε ότι:
και παίρνουμε ότι: .
. .
. :
: παίρνουμε ότι
παίρνουμε ότι  , οπότε
, οπότε  .
. και παίρνουμε ότι
και παίρνουμε ότι 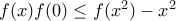 .
. τείνει στο άπειρο. Λόγω του ότι
τείνει στο άπειρο. Λόγω του ότι  και το γεγονός ότι το
και το γεγονός ότι το  θα τείνει στο μείον άπειρο, έχουμε ότι το
θα τείνει στο μείον άπειρο, έχουμε ότι το 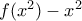 θα τείνει στο μείον άπειρο, άρα και το
θα τείνει στο μείον άπειρο, άρα και το  θα τείνει στο μείον άπειρο. Αφού
θα τείνει στο μείον άπειρο. Αφού  συμπεραίνουμε ότι όταν το
συμπεραίνουμε ότι όταν το  τείνει στο άπειρο το
τείνει στο άπειρο το  θα τείνει στο μείον άπειρο.
θα τείνει στο μείον άπειρο.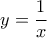 .
. .
. τείνει στο άπειρο το δεξί μέλος θα τείνει στο μείον άπειρο. Όμως λόγω του ότι τα
τείνει στο άπειρο το δεξί μέλος θα τείνει στο μείον άπειρο. Όμως λόγω του ότι τα  και
και  θα τείνουν στο μείον άπειρο έχουμε ότι το γινόμενό τους θα τείνει στο άπειρο, άρα η ανισοτική σχέση δεν θα ισχύει, άτοπο.
θα τείνουν στο μείον άπειρο έχουμε ότι το γινόμενό τους θα τείνει στο άπειρο, άρα η ανισοτική σχέση δεν θα ισχύει, άτοπο. .
. και παίρνουμε ότι
και παίρνουμε ότι  , οπότε
, οπότε  για
για  .
. και
και  .
. . Οπότε:
. Οπότε: . Όμως αφού
. Όμως αφού  και
και  , έχουμε ότι
, έχουμε ότι  .
. και παίρνουμε ότι
και παίρνουμε ότι  . Από αυτό παίρνουμε ότι
. Από αυτό παίρνουμε ότι  για
για  .
. έχουμε ότι
έχουμε ότι  .
.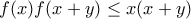 , αφού
, αφού  , άρα
, άρα  .
. για κάποιο
για κάποιο  , τότε
, τότε 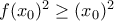 . Επομένως θα πρέπει
. Επομένως θα πρέπει  και αφού το
και αφού το  θα πρέπει
θα πρέπει  (αφού
(αφού  ).
).  για κάθε πραγματικό αριθμό
για κάθε πραγματικό αριθμό  .
.Για
 προκύπτει από την αρχική για κάθε
προκύπτει από την αρχική για κάθε  :
:
 και
και  στην
στην  διαδοχικά προκύπτουν:
διαδοχικά προκύπτουν:
 η αρχική
η αρχική  δίνει:
δίνει: 

 και
και  η αρχική γράφεται:
η αρχική γράφεται: ή
ή 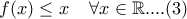
 έχουμε
έχουμε 
 άρα τελικά προκύπτει:
άρα τελικά προκύπτει: 
 ενώ η
ενώ η  γράφεται:
γράφεται:
 και
και  στην αρχική προκύπτει:
στην αρχική προκύπτει:
 με
με  τότε θα έχουμε:
τότε θα έχουμε: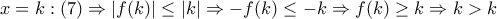 το οποίο είναι άτοπο.Επομένως
το οποίο είναι άτοπο.Επομένως 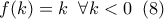
 προκύπτει ότι
προκύπτει ότι 
 για τις οποίες ισχύει
για τις οποίες ισχύει  για κάθε
για κάθε 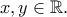
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης