 ώστε για κάθε
ώστε για κάθε  να ισχύει
να ισχύει
Η άσκηση αυτήν ήταν θέμα από μαθηματικο διαγωνισμό στην Αμερική το 2003
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
 ώστε
ώστε  . Επίσης υπάρχει το ζήτημα αν
. Επίσης υπάρχει το ζήτημα αν  ή όχι μιας και η απάντηση ίσως και να αλλάζει.
ή όχι μιας και η απάντηση ίσως και να αλλάζει.Η ακριβής εκφώνηση είναι:
 συμβολίζει το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις
συμβολίζει το σύνολο των θετικών ακεραίων. Να βρείτε όλες τις συναρτήσεις 
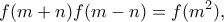 για
για  .
.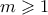 έχω:
έχω:


 είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο. έχω:
έχω:


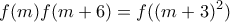
 είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο. είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο. είναι τέλειο τετράγωνο για κάθε
είναι τέλειο τετράγωνο για κάθε  .
. περιττό (
περιττό ( ) έχω
) έχω  και επειδή τα
και επειδή τα 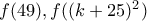 είναι τέλεια τετράγωνα, το ίδιο ισχύει και για το
είναι τέλεια τετράγωνα, το ίδιο ισχύει και για το  . Έχει επίσης αποδειχθεί ότι
. Έχει επίσης αποδειχθεί ότι  τέλειο τετράγωνο και άρα
τέλειο τετράγωνο και άρα  τέλειο τετράγωνο για κάθε περιττό
τέλειο τετράγωνο για κάθε περιττό  . Ομοίως
. Ομοίως  τέλειο τετράγωνο για κάθε άρτιο
τέλειο τετράγωνο για κάθε άρτιο  .
.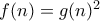 για κάποια συνάρτηση
για κάποια συνάρτηση 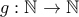 . Καταλήγω όμως στην
. Καταλήγω όμως στην  για κάθε
για κάθε  .
.  πρέπει επίσης να είναι τέλειο τετράγωνο για κάθε
πρέπει επίσης να είναι τέλειο τετράγωνο για κάθε  . Δηλαδή το
. Δηλαδή το  να είναι τέλεια τέταρτη δύναμη. Επαγωγικά (στο
να είναι τέλεια τέταρτη δύναμη. Επαγωγικά (στο  ), για κάθε
), για κάθε  και κάθε
και κάθε  το
το  είναι τέλεια δύναμη με εκθέτη
είναι τέλεια δύναμη με εκθέτη 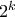 . Απαραίτητα πρέπει
. Απαραίτητα πρέπει  . (Επειδή αν
. (Επειδή αν  τότε το
τότε το  δεν μπορεί να γραφτεί στην μορφή
δεν μπορεί να γραφτεί στην μορφή  αφού
αφού  .)
.) για κάθε
για κάθε  .
. .
.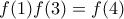 ,
, δηλαδή
δηλαδή 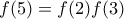 .Επιπλέον,
.Επιπλέον, δηλαδή
δηλαδή  .
. ,
,
 και
και  ,οι οποίες ισχύουν (μαζί-αθροιστικά) για όλους τους αριθμούς
,οι οποίες ισχύουν (μαζί-αθροιστικά) για όλους τους αριθμούς  .Αν βάλω στην αρχική
.Αν βάλω στην αρχική  και χρησιμοποιήσω τους παραπάνω τύπους για το δεξί μέλος ,παίρνω
και χρησιμοποιήσω τους παραπάνω τύπους για το δεξί μέλος ,παίρνω 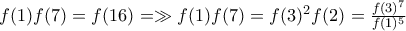 ,ενώ για
,ενώ για  καταλήγω στην
καταλήγω στην  και αξιοποιώντας τις 2 τελευταίες
και αξιοποιώντας τις 2 τελευταίες  .Χρειάζομαι άλλη μια σχέση που θα αποδείξει ότι τελικώς
.Χρειάζομαι άλλη μια σχέση που θα αποδείξει ότι τελικώς  .Μια τέτοια είναι η
.Μια τέτοια είναι η  .Άρα
.Άρα  και από τους τύπους,
και από τους τύπους,  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες