
(Δεν ξέρω την προέλευσή της. Εμένα μου την έστειλε κάποιος από Ρουμανία, ζητώντας λύση. Έκανα μία πολλή σύντομη.)
Συντονιστές: achilleas, emouroukos, silouan

Ας δούμε μια λύση.Mihalis_Lambrou έγραψε: ↑Κυρ Ιαν 06, 2019 2:15 pmΝα επιλυθεί στους πραγματικούς το σύστημα
(Δεν ξέρω την προέλευσή της. Εμένα μου την έστειλε κάποιος από Ρουμανία, ζητώντας λύση. Έκανα μία πολλή σύντομη.)

![\theta _{i}\in [0,\pi ] \theta _{i}\in [0,\pi ]](/forum/ext/geomar/texintegr/latexrender/pictures/38eed5b3ea50f13e2ff1fa8d73269966.png)






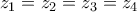


Κάπου στην αρχική σελίδα είναι γραμμένο το εξής:Τσιαλας Νικολαος έγραψε: ↑Κυρ Ιαν 06, 2019 2:28 pmΚύριε Μιχάλη καλησπέρα και καλή χρονιά! Έχει πέσει αν θυμάμαι καλά σε κάποιο διαγωνισμό. Είμαι σίγουρος ότι την έχω λύσει με τα παιδιά αλλά δεν θυμάμαι την προελευση της. Αύριο θα προσπαθήσω να την βρω


 είναι ανάλογα.
είναι ανάλογα.
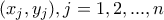 είναι ανάλογα.
είναι ανάλογα.
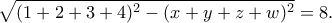

 δίνει
δίνει 
Η δική μου λύση. Κατά βάθος είναι, κρυφά, ουσιαστικά η ίδια με τις τρεις προηγούμενες.
 .
. , αντίστοιχα, και το δεξί
, αντίστοιχα, και το δεξί  . Παρατηρούμε ότι
. Παρατηρούμε ότι  , δηλαδή τα διανύσματα αριστερά έχουν συνολικό μήκος όσο το δεξί, που σημαίνει ότι έχουμε περίπτωση ισότητας στην τριγωνική ανισότητα. Έπεται ότι τα διανύσματα είναι συνευθειακά. Τα υπόλοιπα απλά (άλλωστε υπάρχουν και στις τρεις παραπάνω λύσεις).
, δηλαδή τα διανύσματα αριστερά έχουν συνολικό μήκος όσο το δεξί, που σημαίνει ότι έχουμε περίπτωση ισότητας στην τριγωνική ανισότητα. Έπεται ότι τα διανύσματα είναι συνευθειακά. Τα υπόλοιπα απλά (άλλωστε υπάρχουν και στις τρεις παραπάνω λύσεις).
![\leqslant \left[ {{{\left( {\sqrt {1 - x} } \right)}^2} + ... + {{\left( {\sqrt {4 - w} } \right)}^2}} \right]\left[ {{{\left( {\sqrt {1 + x} } \right)}^2} + ... + {{\left( {\sqrt {4 + w} } \right)}^2}} \right] = 64. \leqslant \left[ {{{\left( {\sqrt {1 - x} } \right)}^2} + ... + {{\left( {\sqrt {4 - w} } \right)}^2}} \right]\left[ {{{\left( {\sqrt {1 + x} } \right)}^2} + ... + {{\left( {\sqrt {4 + w} } \right)}^2}} \right] = 64.](/forum/ext/geomar/texintegr/latexrender/pictures/7e0cc5b8b620be0041ae73b4f7d8f664.png)

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης