KARKAR έγραψε: ↑Πέμ Ιαν 10, 2019 11:34 am
Από τα σημεία
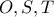
διέρχεται μοναδικός κύκλος . Καταφέραμε και κατασκευάσαμε και ένα τετράγωνο , το
οποίο διέρχεται από τα ίδια σημεία . Συγκρίνετε τα εμβαδά των δύο σχημάτων . Σκεφθείτε αν για οποιαδήποτε
τρία μη συνευθειακά σημεία , μπορούμε να σχεδιάζουμε τετράγωνο με εμβαδόν μεγαλύτερο από του κύκλου.
Αν απαιτήσουμε ότι τα δοθέντα σημεία είναι σε διαφορετικές πλευρές του τε τετραγώνου, τότε έχουμε και "ακραίες συμπεριφορές". Συγκεκριμένα, θα υπάρχουν τότε δύο από τα τρία σημεία που βρίσκονται σε απέναντι πλευρές του τετραγώνου. Αν

η (δοθείσα) απόστασή τους τότε έπεται ότι η πλευρά του τετραγώνου είναι

και άρα το εμβαδόν του είναι

. Μπορούμε όμως να βρούμε περιπτώσεις, για δοθέν

, που το εμβαδόν του κύκλου είναι όσο μεγάλο θέλουμε (να τείνει στο άπειρο). Για παράδειγμα αν τα σημεία είναι τα

, τότε ο κύκλος

έχει τεράστια ακτίνα διότι το τρίγωνο είναι "πεπλατυσμένο". Mάλιστα τείνει στο άπειρο καθώς

. Άρα δεν μπορούμε να βρούμε τετράγωνο εμβαδού μεγαλύτερου του κύκλου.
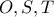 διέρχεται μοναδικός κύκλος . Καταφέραμε και κατασκευάσαμε και ένα τετράγωνο , το
διέρχεται μοναδικός κύκλος . Καταφέραμε και κατασκευάσαμε και ένα τετράγωνο , το 
 είναι ισόπλευρο πλευράς έστω
είναι ισόπλευρο πλευράς έστω  Τότε το εμβαδόν του κύκλου είναι
Τότε το εμβαδόν του κύκλου είναι  και το μέγιστο τετράγωνο έχει εμβαδόν
και το μέγιστο τετράγωνο έχει εμβαδόν  Επειδή όμως,
Επειδή όμως,  θα είναι
θα είναι 
 αλλά μικρότερη από
αλλά μικρότερη από 
 του τριγώνου ισχύει
του τριγώνου ισχύει 
 παράλληλη στην
παράλληλη στην  που τέμνει τα ημικύκλια διαμέτρων
που τέμνει τα ημικύκλια διαμέτρων  στα
στα  αντίστοιχα και κατασκευάζω
αντίστοιχα και κατασκευάζω  με εμβαδόν
με εμβαδόν  και έστω
και έστω  και
και  η ακτίνα του περιγεγραμμένου κύκλου.
η ακτίνα του περιγεγραμμένου κύκλου.  και το εμβαδόν του κύκλου
και το εμβαδόν του κύκλου 

 (
( ), αυτό συμβαίνει για
), αυτό συμβαίνει για 
 και τα ίσα εμβαδά περίπου
και τα ίσα εμβαδά περίπου 
 η (δοθείσα) απόστασή τους τότε έπεται ότι η πλευρά του τετραγώνου είναι
η (δοθείσα) απόστασή τους τότε έπεται ότι η πλευρά του τετραγώνου είναι  και άρα το εμβαδόν του είναι
και άρα το εμβαδόν του είναι  . Μπορούμε όμως να βρούμε περιπτώσεις, για δοθέν
. Μπορούμε όμως να βρούμε περιπτώσεις, για δοθέν  , τότε ο κύκλος
, τότε ο κύκλος  έχει τεράστια ακτίνα διότι το τρίγωνο είναι "πεπλατυσμένο". Mάλιστα τείνει στο άπειρο καθώς
έχει τεράστια ακτίνα διότι το τρίγωνο είναι "πεπλατυσμένο". Mάλιστα τείνει στο άπειρο καθώς  . Άρα δεν μπορούμε να βρούμε τετράγωνο εμβαδού μεγαλύτερου του κύκλου.
. Άρα δεν μπορούμε να βρούμε τετράγωνο εμβαδού μεγαλύτερου του κύκλου.




 Τώρα είναι,
Τώρα είναι, 
