Καλημέρα

.
Σας ευχαριστώ όλους θερμά για την ενασχόληση.
Αρχικά ήθελα να αναφέρω ότι το δεύτερο θεώρημα αντικατάστασης του ορισμένου ολοκλήρωματος δεν υπάρχει στο σχολικό βιβλίο, σχετικά μπορεί κάποιος να μελετήσει το εξαιρετικό άρθρο του συνάδελφου Φάνη Μαργαρώνη στο blog "Εκθέτης" του κυρίου Μαυρογιάννη. Με συγχωρείτε που δεν το ανέφερα από την αρχή.Παρακαλώ για την εύρυθμη λειτουργία του forum να μεταφερθεί το θέμα που άνοιξα στο φάκελο του καθηγητή από τους γενικούς συντονιστές, αν κρίνεται απαραίτητο.
Το δεύτερο θεώρημα αναφέρει ότι:
"Αν μια συνάρτηση

ορισμένη σε ένα διάστημα
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
συνεχώς παραγωγίσιμη με μη μηδενική παράγωγο στο
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
και

συνεχή στο
![g([a,b]) g([a,b])](/forum/ext/geomar/texintegr/latexrender/pictures/dcdca8bc7d28967e18d77bb2d911dd3b.png)
, τότε ισχύει ότι
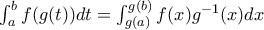
.
Λάμπρο, στο παραπάνω θεώρημα αναφέρομαι , όπου θεωρώ το δοθέν ολοκλήρωμα ως το πρώτο μέλος της παραπάνω ισότητας με
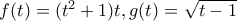
. Ο τρόπος που αναφέρεις με βρίσκει σύμφωνη για τη διδασκαλία του ολοκληρώματος στο λύκειο. Σε πολύ γνωστό βοήθημα που βρήκα όμως το ολοκλήρωμα προτείνεται η αντικατάσταση
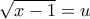
όπως πρωτοέγραψε ο Τόλης , που δεν με παρέπεμψε στο γνωστό θέωρημα του σχολικού (όπως λες και εσύ), αλλά στο 2ο θεώρημα που εκεί γίνεται λάθος εφαρμογή του.
1. Δεν διδάσκουμε με αυτό που λέμε και κάνουμε. Διδάσκουμε με αυτό που είμαστε.
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
 να λυθεί με την αντικατάσταση
να λυθεί με την αντικατάσταση  δεδομένου ότι για την συνάρτηση
δεδομένου ότι για την συνάρτηση  δεν ισχύει ότι η g'(x) είναι μη μηδενική στο
δεν ισχύει ότι η g'(x) είναι μη μηδενική στο ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) αφού δεν είναι παραγωγίσιμη στο
αφού δεν είναι παραγωγίσιμη στο  και υπάρχει πρόβλημα στην εφαρμογή του δεύτερου θεωρήματος αντικατάστασης στα ορισμένα ολοκληρώματα;
και υπάρχει πρόβλημα στην εφαρμογή του δεύτερου θεωρήματος αντικατάστασης στα ορισμένα ολοκληρώματα;


 .
.![g:[c,d] \to [a,b] g:[c,d] \to [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/a3b2330e9525e00a46030e1520a4a573.png) συνεχής στο
συνεχής στο ![[c,d] [c,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c31d2b7df15fa7d119c2f8d13f69e10b.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο 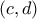 με την
με την  να είναι συνεχής στο
να είναι συνεχής στο ![f:[a,b] \to \mathbb{R} f:[a,b] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/1e32016b6e720735017fcee010f23652.png) . Τότε η
. Τότε η  είναι ολοκληρώσιμη στο
είναι ολοκληρώσιμη στο 
 η
η  είναι παραγωγίσιμη στο 1 όμως η αντίστροφη της
είναι παραγωγίσιμη στο 1 όμως η αντίστροφη της  δεν είναι. Έτσι αποφύγαμε την δυσκολία του κάτω άκρου
δεν είναι. Έτσι αποφύγαμε την δυσκολία του κάτω άκρου ως
ως  και να χρησιμοποιήσεις την συνέχεια όταν
και να χρησιμοποιήσεις την συνέχεια όταν 
 καθώς το γινόμενο
καθώς το γινόμενο  είναι συνεχής αλλά η
είναι συνεχής αλλά η 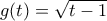 δεν έχει συνεχή παράγωγο.
δεν έχει συνεχή παράγωγο.  ποια είναι η
ποια είναι η  και ποια είναι η
και ποια είναι η  ;
;  τότε αρκεί να βρεις μια
τότε αρκεί να βρεις μια ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) ώστε
ώστε  ,
, ![g([a,b]) g([a,b])](/forum/ext/geomar/texintegr/latexrender/pictures/dcdca8bc7d28967e18d77bb2d911dd3b.png)
 συνεχής στο
συνεχής στο  .
.  έχουμε
έχουμε  και
και  συνεχής. Επίσης
συνεχής. Επίσης ![g([a,b])=[1,2] g([a,b])=[1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/402b9f8356edf0c1ca472d82fd61ea48.png) . Τότε παίρνουμε
. Τότε παίρνουμε 
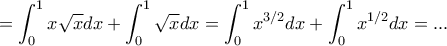
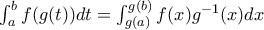 .
.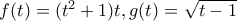 . Ο τρόπος που αναφέρεις με βρίσκει σύμφωνη για τη διδασκαλία του ολοκληρώματος στο λύκειο. Σε πολύ γνωστό βοήθημα που βρήκα όμως το ολοκλήρωμα προτείνεται η αντικατάσταση
. Ο τρόπος που αναφέρεις με βρίσκει σύμφωνη για τη διδασκαλία του ολοκληρώματος στο λύκειο. Σε πολύ γνωστό βοήθημα που βρήκα όμως το ολοκλήρωμα προτείνεται η αντικατάσταση 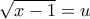 όπως πρωτοέγραψε ο Τόλης , που δεν με παρέπεμψε στο γνωστό θέωρημα του σχολικού (όπως λες και εσύ), αλλά στο 2ο θεώρημα που εκεί γίνεται λάθος εφαρμογή του.
όπως πρωτοέγραψε ο Τόλης , που δεν με παρέπεμψε στο γνωστό θέωρημα του σχολικού (όπως λες και εσύ), αλλά στο 2ο θεώρημα που εκεί γίνεται λάθος εφαρμογή του. , να βρεθεί το
, να βρεθεί το  με την προυπόθεση ότι η
με την προυπόθεση ότι η  είναι συνεχής , θέτοντας
είναι συνεχής , θέτοντας  και λοιπά" ποιο θεώρημα χρησιμοποιούμε;
και λοιπά" ποιο θεώρημα χρησιμοποιούμε;