 για την οποία ισχύει:
για την οποία ισχύει:
Να δειχθεί ότι
 .
.Συντονιστής: emouroukos
 για την οποία ισχύει:
για την οποία ισχύει:
 .
.
Μάλλον την έχουμε ξαναδεί, την ίδια ή παρόμοια.Tolaso J Kos έγραψε: ↑Κυρ Ιαν 27, 2019 9:34 amΔίδεται η συνεχής συνάρτησηγια την οποία ισχύει:

Να δειχθεί ότι.
 , έστω
, έστω  άνω φράγμα της
άνω φράγμα της  στο
στο ![[0,\, x] [0,\, x]](/forum/ext/geomar/texintegr/latexrender/pictures/7ea70188c8139da1793531a5c1112dde.png) . Έχουμε
. Έχουμε 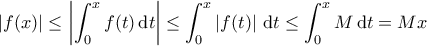
 έχουμε επαγωγικά
έχουμε επαγωγικά  . Άρα
. Άρα  . Όμοια για
. Όμοια για  και προφανές από την αρχική για
και προφανές από την αρχική για  (άλλωστε βγαίνει από από συνέχεια από τα προηγούμενα).
(άλλωστε βγαίνει από από συνέχεια από τα προηγούμενα).Να σημειώσω ότι δεν χρειάζεται η συνέχεια της συνάρτησης.Mihalis_Lambrou έγραψε: ↑Κυρ Ιαν 27, 2019 11:28 amΜάλλον την έχουμε ξαναδεί, την ίδια ή παρόμοια.Tolaso J Kos έγραψε: ↑Κυρ Ιαν 27, 2019 9:34 amΔίδεται η συνεχής συνάρτησηγια την οποία ισχύει:

Να δειχθεί ότι.
Για σταθερό, έστω
άνω φράγμα της
στο
. Έχουμε
Με χρήση αυτού στην θέση τουέχουμε επαγωγικά
. Άρα
. Όμοια για
και προφανές από την αρχική για
(άλλωστε βγαίνει από από συνέχεια από τα προηγούμενα).
![[0,x] [0,x]](/forum/ext/geomar/texintegr/latexrender/pictures/47e2767cb741a37b889f1968c34f8398.png) η
η ![[x,0] [x,0]](/forum/ext/geomar/texintegr/latexrender/pictures/967b16ccceb41d4895daa1b791e33e8d.png) .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης