Soteris έγραψε: ↑Κυρ Φεβ 10, 2019 1:55 pm
Πρόβλημα 4
Σε μια τάξη

μαθητών δόθηκε ένα διαγώνισμα

προβλημάτων. Γνωρίζουμε ότι κάθε πρόβλημα λύθηκε σωστά από τουλάχιστον
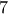
μαθητές.
Να αποδείξετε ότι υπάρχει ζεύγος

μαθητών, ώστε κάθε πρόβλημα να λύθηκε σωστά από τουλάχιστον ένα μαθητή απ’ αυτούς.
Έστω

οι μαθητές και

τα προβλήματα.
Έστω

τα
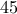
διαφορετικά ζεύγη που μπορούν να κάνουν όλοι οι μαθητές.
Μετράμε τις δυάδες
![[r_i, p_j] [r_i, p_j]](/forum/ext/geomar/texintegr/latexrender/pictures/d1b2c4db6318e6f99b3670ff84e46826.png)
, όπου μια δυάδα υφίσταται όταν ένας τουλάχιστον από τους μαθητές του ζεύγους

έχει λύσει το πρόβλημα

.
Για κάθε πρόβλημα τα ζεύγη μαθητών είναι είναι τουλάχιστον

(αφαιρούμε το

γιατί διπλομετρούμε τα ζευγάρια που έχουν δύο μαθητές που έλυσαν και οι δύο το πρόβλημα), άρα συνολικά έχουμε τουλάχιστον

δυάδες, με ισότητα αν όλα τα προβλήματα λύθηκαν ακριβώς από

μαθητές.
Από την άλλη έχουμε
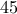
ζεύγη και

. Άρα αν κάποιο ζευγάρι μαθητών έλυσε λιγότερα από

προβλήματα, θα είχαμε κάποιο άλλο ζευγάρι με

προβλήματα και το ζητούμενο έπεται. Έστω λοιπόν πως όλα τα ζευγάρια έλυσαν

προβλήματα. Για να ισχύει αυτό πρέπει κάθε πρόβλημα να λύθηκε από ακριβώς

μαθητές.
Επειδή οι δυάδες (μαθητής-ένα πρόβλημα που έλυσε ο συγκεκριμένος μαθητής), είναι

, και

, υπάρχει μαθητής που έλυσε το πολύ

προβλήματα.
Έστω πως ο μαθητής

δεν έλυσε τα προβλήματα

.
Για καθένα από τα παραπάνω

προβλήματα δεν μπορεί να υπάρχει μαθητής

, ώστε ο

να μην έλυσε

προβλήματα από αυτά, καθώς σε αυτή την περίπτωση θα είχαμε πως το ζεύγος μαθητών

και

έλυσε το πολύ

προβλήματα.
Με άλλα λόγια στα προβλήματα

και

, οι άλλοι δύο μαθητές που δεν έλυσαν το καθένα από αυτά (εκτός του

υπάρχουν άλλοι δύο στο καθένα αφού κάθε πρόβλημα δεν λύθηκε από 3 άτομα), πρέπει να μην είναι κοινοί. Έτσι όμως μαζεύονται

μαθητές, από τους υπόλοιπους

, άτοπο.
Άρα το ζητούμενο έπεται!
Edit: Μερικές Βελτιώσεις...
 με
με  ως εξής:
ως εξής:
 και
και 

 και
και 

 και
και 
 .
. , ώστε ο αριθμός
, ώστε ο αριθμός 
 .
. εγγεγραμμένο σε κύκλο με κέντρο
εγγεγραμμένο σε κύκλο με κέντρο  και
και  το ύψος του (το σημείο
το ύψος του (το σημείο  είναι το ίχνος του ύψους πάνω στην
είναι το ίχνος του ύψους πάνω στην  ). Έστω
). Έστω  το σημείο τομής της
το σημείο τομής της  με την
με την  . Θεωρούμε
. Θεωρούμε  τα μέσα των τμημάτων
τα μέσα των τμημάτων  και
και  , αντίστοιχα. Φέρουμε την ευθεία
, αντίστοιχα. Φέρουμε την ευθεία  και ονομάζουμε
και ονομάζουμε  το σημείο τομής της με την
το σημείο τομής της με την  . Αν
. Αν  τα κέντρα των περιγεγραμμένων κύκλων των τριγώνων
τα κέντρα των περιγεγραμμένων κύκλων των τριγώνων  , αντίστοιχα, να αποδείξετε ότι
, αντίστοιχα, να αποδείξετε ότι  .
. μαθητών δόθηκε ένα διαγώνισμα
μαθητών δόθηκε ένα διαγώνισμα  προβλημάτων. Γνωρίζουμε ότι κάθε πρόβλημα λύθηκε σωστά από τουλάχιστον
προβλημάτων. Γνωρίζουμε ότι κάθε πρόβλημα λύθηκε σωστά από τουλάχιστον 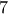 μαθητές.
μαθητές.  μαθητών, ώστε κάθε πρόβλημα να λύθηκε σωστά από τουλάχιστον ένα μαθητή απ’ αυτούς.
μαθητών, ώστε κάθε πρόβλημα να λύθηκε σωστά από τουλάχιστον ένα μαθητή απ’ αυτούς.
 :
:

 .
. 
 , άρα
, άρα  ή
ή 
 οι μαθητές και
οι μαθητές και  τα προβλήματα.
τα προβλήματα. τα
τα 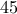 διαφορετικά ζεύγη που μπορούν να κάνουν όλοι οι μαθητές.
διαφορετικά ζεύγη που μπορούν να κάνουν όλοι οι μαθητές. ![[r_i, p_j] [r_i, p_j]](/forum/ext/geomar/texintegr/latexrender/pictures/d1b2c4db6318e6f99b3670ff84e46826.png) , όπου μια δυάδα υφίσταται όταν ένας τουλάχιστον από τους μαθητές του ζεύγους
, όπου μια δυάδα υφίσταται όταν ένας τουλάχιστον από τους μαθητές του ζεύγους  έχει λύσει το πρόβλημα
έχει λύσει το πρόβλημα  .
. (αφαιρούμε το
(αφαιρούμε το  γιατί διπλομετρούμε τα ζευγάρια που έχουν δύο μαθητές που έλυσαν και οι δύο το πρόβλημα), άρα συνολικά έχουμε τουλάχιστον
γιατί διπλομετρούμε τα ζευγάρια που έχουν δύο μαθητές που έλυσαν και οι δύο το πρόβλημα), άρα συνολικά έχουμε τουλάχιστον  δυάδες, με ισότητα αν όλα τα προβλήματα λύθηκαν ακριβώς από
δυάδες, με ισότητα αν όλα τα προβλήματα λύθηκαν ακριβώς από  μαθητές.
μαθητές. . Άρα αν κάποιο ζευγάρι μαθητών έλυσε λιγότερα από
. Άρα αν κάποιο ζευγάρι μαθητών έλυσε λιγότερα από  προβλήματα, θα είχαμε κάποιο άλλο ζευγάρι με
προβλήματα, θα είχαμε κάποιο άλλο ζευγάρι με  προβλήματα και το ζητούμενο έπεται. Έστω λοιπόν πως όλα τα ζευγάρια έλυσαν
προβλήματα και το ζητούμενο έπεται. Έστω λοιπόν πως όλα τα ζευγάρια έλυσαν  , και
, και  , υπάρχει μαθητής που έλυσε το πολύ
, υπάρχει μαθητής που έλυσε το πολύ  προβλήματα.
προβλήματα. δεν έλυσε τα προβλήματα
δεν έλυσε τα προβλήματα  .
. προβλήματα δεν μπορεί να υπάρχει μαθητής
προβλήματα δεν μπορεί να υπάρχει μαθητής  , ώστε ο
, ώστε ο  να μην έλυσε
να μην έλυσε  προβλήματα από αυτά, καθώς σε αυτή την περίπτωση θα είχαμε πως το ζεύγος μαθητών
προβλήματα από αυτά, καθώς σε αυτή την περίπτωση θα είχαμε πως το ζεύγος μαθητών  προβλήματα.
προβλήματα. και
και  , οι άλλοι δύο μαθητές που δεν έλυσαν το καθένα από αυτά (εκτός του
, οι άλλοι δύο μαθητές που δεν έλυσαν το καθένα από αυτά (εκτός του  μαθητές, από τους υπόλοιπους
μαθητές, από τους υπόλοιπους  , άτοπο.
, άτοπο.
 όπου το
όπου το  φορές ομοίως
φορές ομοίως  όπου το 4 επαναλαμβάνεται
όπου το 4 επαναλαμβάνεται  φορές όμως
φορές όμως  άρα
άρα  όπου το
όπου το  φορές και τώρα προφανώς
φορές και τώρα προφανώς  (χρεισιμοποίησα τα αντίστοιχα αγγλικά γράμματα για συντομία)
(χρεισιμοποίησα τα αντίστοιχα αγγλικά γράμματα για συντομία) και άλλο το
και άλλο το 
 (
( ), οπότε αφού
), οπότε αφού  εύκολα προκύπτει ότι
εύκολα προκύπτει ότι  .
. , για
, για  .
. έχουμε ότι
έχουμε ότι  .
. . Θα δείξουμε ότι ισχύει και για
. Θα δείξουμε ότι ισχύει και για  .
. , που ισχύει αφού
, που ισχύει αφού  .
. .
. , άρα
, άρα 

 ... (
... (  την προβολή του
την προβολή του  στην
στην  .Τα
.Τα  είναι ομοκυκλικά,οπότε αν δειχτεί ότι και τα
είναι ομοκυκλικά,οπότε αν δειχτεί ότι και τα  ομοκυκλικά,ουσιαστικά από ριζικούς άξονες έχει τελειώσει.Άρα αρκεί η τομή του
ομοκυκλικά,ουσιαστικά από ριζικούς άξονες έχει τελειώσει.Άρα αρκεί η τομή του  με την
με την  ,έστω
,έστω  να ταυτίζεται με το
να ταυτίζεται με το  .Αρκεί
.Αρκεί  με
με  το μέσο της
το μέσο της  η τομή
η τομή  και
και  η τομή των
η τομή των  από ίσες εγγεγραμμένες τα
από ίσες εγγεγραμμένες τα  είναι συνευθειακά.Άρα το
είναι συνευθειακά.Άρα το  ανήκει στην πολική του
ανήκει στην πολική του  ,δηλαδή είναι η
,δηλαδή είναι η  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. τέμνει την
τέμνει την  στο
στο  .
. .
.  .
. είναι εγγράψιμο, τότε θα είχα
είναι εγγράψιμο, τότε θα είχα  , και το ζητούμενο έπεται.
, και το ζητούμενο έπεται. .
. .
. .
. , συνεπώς το
, συνεπώς το  είναι ορθόκεντρο του
είναι ορθόκεντρο του  .
. , είναι
, είναι  .
. , ή ισοδύναμα
, ή ισοδύναμα  (1).
(1). (1).
(1). με διατέμνουσα την
με διατέμνουσα την  παίρνουμε
παίρνουμε  .
. .
. , οπότε θα προκύψει
, οπότε θα προκύψει  .
. .
. , οπότε
, οπότε  (2).
(2). , και η απόδειξη (επιτέλους) ολοκληρώθηκε.
, και η απόδειξη (επιτέλους) ολοκληρώθηκε. προβλήματα, άρα από περιστεροφωλιά υπάρχει μαθητής
προβλήματα, άρα από περιστεροφωλιά υπάρχει μαθητής  που έλυσε τουλάχιστον
που έλυσε τουλάχιστον  . Μένουν το πολύ
. Μένουν το πολύ  προβλήματα και πρέπει να βρούμε έναν από τους υπόλοιπους
προβλήματα και πρέπει να βρούμε έναν από τους υπόλοιπους  άτομα που δεν έλυσαν κάποιο από αυτά. Άρα υπάρχει και κάποιος που έλυσε όλα όσα δεν έλυσε ο
άτομα που δεν έλυσαν κάποιο από αυτά. Άρα υπάρχει και κάποιος που έλυσε όλα όσα δεν έλυσε ο  να αναφέρω ακόμη δύο τρόπους που έκαναν μαθητές μας.
να αναφέρω ακόμη δύο τρόπους που έκαναν μαθητές μας.  . Ο δεύτερος είναι να αποδειχθεί επαγωγικά η σχέση
. Ο δεύτερος είναι να αποδειχθεί επαγωγικά η σχέση  . Εδώ θέλει λίγη περισσότερη προσοχή. Στο επαγωγικό βήμα έχουμε
. Εδώ θέλει λίγη περισσότερη προσοχή. Στο επαγωγικό βήμα έχουμε
 είναι άρτιος.
είναι άρτιος.