ΑΡΧΙΜΗΔΗΣ 2018-2019
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
ΑΡΧΙΜΗΔΗΣ 2018-2019
Αγαπητοί φίλοι,
Αυτή την ώρα διεξάγεται η Εθνική Μαθηματική Ολυμπιάδα "Ο Αρχιμήδης". Αφού ευχηθώ καλή επιτυχία και καλά αποτελέσματα στους μαθητές μας θα ήθελα να παρακαλέσω τα θέματα και οι λύσεις τους να σχολιαστούν μετά το πέρας του διαγωνισμού δηλαδή μετά τη 1 το μεσημέρι.
Αλέξανδρος Συγκελάκης
Αυτή την ώρα διεξάγεται η Εθνική Μαθηματική Ολυμπιάδα "Ο Αρχιμήδης". Αφού ευχηθώ καλή επιτυχία και καλά αποτελέσματα στους μαθητές μας θα ήθελα να παρακαλέσω τα θέματα και οι λύσεις τους να σχολιαστούν μετά το πέρας του διαγωνισμού δηλαδή μετά τη 1 το μεσημέρι.
Αλέξανδρος Συγκελάκης
Αλέξανδρος Συγκελάκης
Λέξεις Κλειδιά:
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Θέματα Μικρών
Πρόβλημα 1: Να βρείτε όλες τις τριάδες πραγματικών αριθμών που είναι λύσεις του συστήματος
που είναι λύσεις του συστήματος


Πρόβλημα 2: Δίνεται τετράπλευρο εγγεγραμμένο σε κύκλο κέντρου
εγγεγραμμένο σε κύκλο κέντρου  . Η κάθετη στο μέσον Ε της πλευράς
. Η κάθετη στο μέσον Ε της πλευράς  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την πλευρά
τέμνει την πλευρά  για δεύτερη φορά στο σημείο
για δεύτερη φορά στο σημείο  και την ευθεία
και την ευθεία 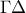 σε σημείο
σε σημείο  διαφορετικό του
διαφορετικό του  . Η ευθεία
. Η ευθεία  τέμνει την ευθεία
τέμνει την ευθεία 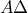 στο σημείο
στο σημείο  και την ευθεία
και την ευθεία  στο σημείο
στο σημείο 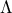 . Να αποδείξετε ότι τα σημεία
. Να αποδείξετε ότι τα σημεία  είναι ομοκυκλικά, δηλαδή ανήκουν στον ίδιο κύκλο.
είναι ομοκυκλικά, δηλαδή ανήκουν στον ίδιο κύκλο.
Πρόβλημα 3: Να προσδιορίσετε όλους τους θετικούς ακεραίους οι οποίοι είναι ίσοι με 13 φορές το άθροισμα των ψηφίων τους.
Πρόβλημα 4: Στον πίνακα είναι γραμμένοι οι θετικοί ακέραιοι . Ο Γιάννης και η Μαρία έχουν το δικαίωμα να κάνουν μαζί την επόμενη κίνηση:
. Ο Γιάννης και η Μαρία έχουν το δικαίωμα να κάνουν μαζί την επόμενη κίνηση:
Επιλέγουν δύο αριθμούς από αυτούς που είναι γραμμένοι στον πίνακα και τους αντικαθιστούν με τους αριθμούς
από αυτούς που είναι γραμμένοι στον πίνακα και τους αντικαθιστούν με τους αριθμούς  και
και  .
.
Ο Γιάννης ισχυρίζεται ότι μετά από πεπερασμένο πλήθος τέτοιων κινήσεων μπορούν να τριπλασιαστούν όλοι οι αριθμοί του πίνακα, δηλαδή να προκύψουν οι αριθμοί: . Η Μαρία σκέπτεται λίγο και του απαντά ότι αυτό δεν είναι δυνατό να γίνει. Ποιος από τους δύο έχει δίκιο και γιατί;
. Η Μαρία σκέπτεται λίγο και του απαντά ότι αυτό δεν είναι δυνατό να γίνει. Ποιος από τους δύο έχει δίκιο και γιατί;
Θέματα Μεγάλων
Πρόβλημα 1: Η ακολουθία έχει πρώτο όρο
έχει πρώτο όρο  και ορίζεται αναδρομικά από τον τύπο:
και ορίζεται αναδρομικά από τον τύπο:

Να υπολογίσετε το γενικό όρο και να βρείτε τη μεγαλύτερη δύναμη του
και να βρείτε τη μεγαλύτερη δύναμη του  που διαιρεί τον όρο
που διαιρεί τον όρο  όπου
όπου 
Πρόβλημα 2: Δίνεται τρίγωνο εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  με
με  και έστω
και έστω  το μέσο του μικρού τόξου
το μέσο του μικρού τόξου  . Η ευθεία
. Η ευθεία 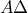 τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  και ο περιγεγραμμένος κύκλος του τριγώνου
και ο περιγεγραμμένος κύκλος του τριγώνου  (έστω
(έστω 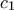 ) τέμνει την
) τέμνει την  για δεύτερη φορά στο σημείο
για δεύτερη φορά στο σημείο  . Αν ο περιγεγραμμένος κύκλος του τριγώνου
. Αν ο περιγεγραμμένος κύκλος του τριγώνου  (έστω
(έστω  ) τέμνει για δεύτερη φορά την
) τέμνει για δεύτερη φορά την  στο σημείο
στο σημείο  , να αποδείξετε ότι
, να αποδείξετε ότι  .
.
Πρόβλημα 3: Να βρείτε όλα τα ζεύγη θετικών ρητών αριθμών που ικανοποιούν την εξίσωση
θετικών ρητών αριθμών που ικανοποιούν την εξίσωση

Πρόβλημα 4: Θεωρούμε ορθογώνιο με
με  , το οποίο υποδιαιρούμε με παράλληλες ευθείες προς τις πλευρές του σε
, το οποίο υποδιαιρούμε με παράλληλες ευθείες προς τις πλευρές του σε  μοναδιαία τετράγωνα. Αρχικά τοποθετούμε από ένα μαύρο πιόνι σε
μοναδιαία τετράγωνα. Αρχικά τοποθετούμε από ένα μαύρο πιόνι σε  μοναδιαία τετράγωνα και στη συνέχεια προσπαθούμε να γεμίσουμε τον πίνακα με μαύρα πιόνια εκτελώντας την παρακάτω επιτρεπόμενη κίνηση:
μοναδιαία τετράγωνα και στη συνέχεια προσπαθούμε να γεμίσουμε τον πίνακα με μαύρα πιόνια εκτελώντας την παρακάτω επιτρεπόμενη κίνηση:
Αν ένα κενό μοναδιαίο τετράγωνο έχει κοινή πλευρά με δύο τουλάχιστον μοναδιαία τετράγωνα κατειλημμένα με μαύρο πιόνι, τότε τοποθετούμε και σε αυτό το μοναδιαίο τετράγωνο ένα μαύρο πιόνι
Να βρείτε την ελάχιστη δυνατή τιμή του αριθμού των μαύρων πιονιών που πρέπει και αρκεί να υπάρχουν σε μια αρχική τοποθέτηση, έτσι ώστε μετά από πεπερασμένο πλήθος διαδοχικών εφαρμογών της επιτρεπόμενης κίνησης να γεμίσει το ορθογώνιο με μαύρα πιόνια.
των μαύρων πιονιών που πρέπει και αρκεί να υπάρχουν σε μια αρχική τοποθέτηση, έτσι ώστε μετά από πεπερασμένο πλήθος διαδοχικών εφαρμογών της επιτρεπόμενης κίνησης να γεμίσει το ορθογώνιο με μαύρα πιόνια.
Πρόβλημα 1: Να βρείτε όλες τις τριάδες πραγματικών αριθμών
 που είναι λύσεις του συστήματος
που είναι λύσεις του συστήματος

Πρόβλημα 2: Δίνεται τετράπλευρο
 εγγεγραμμένο σε κύκλο κέντρου
εγγεγραμμένο σε κύκλο κέντρου  . Η κάθετη στο μέσον Ε της πλευράς
. Η κάθετη στο μέσον Ε της πλευράς  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  . Ο περιγεγραμμένος κύκλος του τριγώνου
. Ο περιγεγραμμένος κύκλος του τριγώνου  τέμνει την πλευρά
τέμνει την πλευρά  για δεύτερη φορά στο σημείο
για δεύτερη φορά στο σημείο  και την ευθεία
και την ευθεία 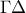 σε σημείο
σε σημείο  διαφορετικό του
διαφορετικό του  . Η ευθεία
. Η ευθεία  τέμνει την ευθεία
τέμνει την ευθεία 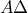 στο σημείο
στο σημείο  και την ευθεία
και την ευθεία  στο σημείο
στο σημείο 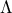 . Να αποδείξετε ότι τα σημεία
. Να αποδείξετε ότι τα σημεία  είναι ομοκυκλικά, δηλαδή ανήκουν στον ίδιο κύκλο.
είναι ομοκυκλικά, δηλαδή ανήκουν στον ίδιο κύκλο. Πρόβλημα 3: Να προσδιορίσετε όλους τους θετικούς ακεραίους οι οποίοι είναι ίσοι με 13 φορές το άθροισμα των ψηφίων τους.
Πρόβλημα 4: Στον πίνακα είναι γραμμένοι οι θετικοί ακέραιοι
 . Ο Γιάννης και η Μαρία έχουν το δικαίωμα να κάνουν μαζί την επόμενη κίνηση:
. Ο Γιάννης και η Μαρία έχουν το δικαίωμα να κάνουν μαζί την επόμενη κίνηση: Επιλέγουν δύο αριθμούς
 από αυτούς που είναι γραμμένοι στον πίνακα και τους αντικαθιστούν με τους αριθμούς
από αυτούς που είναι γραμμένοι στον πίνακα και τους αντικαθιστούν με τους αριθμούς  και
και  .
. Ο Γιάννης ισχυρίζεται ότι μετά από πεπερασμένο πλήθος τέτοιων κινήσεων μπορούν να τριπλασιαστούν όλοι οι αριθμοί του πίνακα, δηλαδή να προκύψουν οι αριθμοί:
 . Η Μαρία σκέπτεται λίγο και του απαντά ότι αυτό δεν είναι δυνατό να γίνει. Ποιος από τους δύο έχει δίκιο και γιατί;
. Η Μαρία σκέπτεται λίγο και του απαντά ότι αυτό δεν είναι δυνατό να γίνει. Ποιος από τους δύο έχει δίκιο και γιατί; Θέματα Μεγάλων
Πρόβλημα 1: Η ακολουθία
 έχει πρώτο όρο
έχει πρώτο όρο  και ορίζεται αναδρομικά από τον τύπο:
και ορίζεται αναδρομικά από τον τύπο:
Να υπολογίσετε το γενικό όρο
 και να βρείτε τη μεγαλύτερη δύναμη του
και να βρείτε τη μεγαλύτερη δύναμη του  που διαιρεί τον όρο
που διαιρεί τον όρο  όπου
όπου 
Πρόβλημα 2: Δίνεται τρίγωνο
 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  με
με  και έστω
και έστω  το μέσο του μικρού τόξου
το μέσο του μικρού τόξου  . Η ευθεία
. Η ευθεία 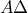 τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  και ο περιγεγραμμένος κύκλος του τριγώνου
και ο περιγεγραμμένος κύκλος του τριγώνου  (έστω
(έστω 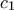 ) τέμνει την
) τέμνει την  για δεύτερη φορά στο σημείο
για δεύτερη φορά στο σημείο  . Αν ο περιγεγραμμένος κύκλος του τριγώνου
. Αν ο περιγεγραμμένος κύκλος του τριγώνου  (έστω
(έστω  ) τέμνει για δεύτερη φορά την
) τέμνει για δεύτερη φορά την  στο σημείο
στο σημείο  , να αποδείξετε ότι
, να αποδείξετε ότι  .
. Πρόβλημα 3: Να βρείτε όλα τα ζεύγη
 θετικών ρητών αριθμών που ικανοποιούν την εξίσωση
θετικών ρητών αριθμών που ικανοποιούν την εξίσωση
Πρόβλημα 4: Θεωρούμε ορθογώνιο
 με
με  , το οποίο υποδιαιρούμε με παράλληλες ευθείες προς τις πλευρές του σε
, το οποίο υποδιαιρούμε με παράλληλες ευθείες προς τις πλευρές του σε  μοναδιαία τετράγωνα. Αρχικά τοποθετούμε από ένα μαύρο πιόνι σε
μοναδιαία τετράγωνα. Αρχικά τοποθετούμε από ένα μαύρο πιόνι σε  μοναδιαία τετράγωνα και στη συνέχεια προσπαθούμε να γεμίσουμε τον πίνακα με μαύρα πιόνια εκτελώντας την παρακάτω επιτρεπόμενη κίνηση:
μοναδιαία τετράγωνα και στη συνέχεια προσπαθούμε να γεμίσουμε τον πίνακα με μαύρα πιόνια εκτελώντας την παρακάτω επιτρεπόμενη κίνηση:Αν ένα κενό μοναδιαίο τετράγωνο έχει κοινή πλευρά με δύο τουλάχιστον μοναδιαία τετράγωνα κατειλημμένα με μαύρο πιόνι, τότε τοποθετούμε και σε αυτό το μοναδιαίο τετράγωνο ένα μαύρο πιόνι
Να βρείτε την ελάχιστη δυνατή τιμή του αριθμού
 των μαύρων πιονιών που πρέπει και αρκεί να υπάρχουν σε μια αρχική τοποθέτηση, έτσι ώστε μετά από πεπερασμένο πλήθος διαδοχικών εφαρμογών της επιτρεπόμενης κίνησης να γεμίσει το ορθογώνιο με μαύρα πιόνια.
των μαύρων πιονιών που πρέπει και αρκεί να υπάρχουν σε μια αρχική τοποθέτηση, έτσι ώστε μετά από πεπερασμένο πλήθος διαδοχικών εφαρμογών της επιτρεπόμενης κίνησης να γεμίσει το ορθογώνιο με μαύρα πιόνια.
τελευταία επεξεργασία από Demetres σε Σάβ Φεβ 23, 2019 8:42 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
Xriiiiistos
- Δημοσιεύσεις: 219
- Εγγραφή: Τρί Μάιος 15, 2018 4:36 pm
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Ωραία είναι τα θέματα !!!
Θέμα 2ο μεγάλων για συντομία
 Από τα εγγράψιμα
Από τα εγγράψιμα  Άρα
Άρα  εγγράψιμο οπότε
εγγράψιμο οπότε  από το εγγράψιμο
από το εγγράψιμο  Και από το εγγράψιμο
Και από το εγγράψιμο  έχουμε
έχουμε  Τα τρίγωνα
Τα τρίγωνα  έχουν όλες τις γωνίες ίσες και επείσης
έχουν όλες τις γωνίες ίσες και επείσης  αφού το
αφού το  μέσο τόξου άρα τα τρίγωνα
μέσο τόξου άρα τα τρίγωνα  είναι ίσα και
είναι ίσα και 
Η άσκηση μας οδηγεί να σκεφτούμε από τυην αρχή για ισότητα τριγώνων αφού από την αρχή έχουμε και πρέπει να βγάλουμε
και πρέπει να βγάλουμε  και με μεταφορές γωνιών από τα εγγράψιμα να βγάλουμε τις γωνίες ίσες (αν είναι ) και σε αυτήν την περίπτωση έτσι λύνεται
και με μεταφορές γωνιών από τα εγγράψιμα να βγάλουμε τις γωνίες ίσες (αν είναι ) και σε αυτήν την περίπτωση έτσι λύνεται
Θέμα 2ο μεγάλων για συντομία

 Από τα εγγράψιμα
Από τα εγγράψιμα  Άρα
Άρα  εγγράψιμο οπότε
εγγράψιμο οπότε  από το εγγράψιμο
από το εγγράψιμο  Και από το εγγράψιμο
Και από το εγγράψιμο  έχουμε
έχουμε  Τα τρίγωνα
Τα τρίγωνα  έχουν όλες τις γωνίες ίσες και επείσης
έχουν όλες τις γωνίες ίσες και επείσης  αφού το
αφού το  μέσο τόξου άρα τα τρίγωνα
μέσο τόξου άρα τα τρίγωνα  είναι ίσα και
είναι ίσα και 
Η άσκηση μας οδηγεί να σκεφτούμε από τυην αρχή για ισότητα τριγώνων αφού από την αρχή έχουμε
 και πρέπει να βγάλουμε
και πρέπει να βγάλουμε  και με μεταφορές γωνιών από τα εγγράψιμα να βγάλουμε τις γωνίες ίσες (αν είναι ) και σε αυτήν την περίπτωση έτσι λύνεται
και με μεταφορές γωνιών από τα εγγράψιμα να βγάλουμε τις γωνίες ίσες (αν είναι ) και σε αυτήν την περίπτωση έτσι λύνεται - Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Θέματα μικρών τάξεων.
Πρόβλημα 1
Να βρείτε όλες τις τριάδες πραγματικών αριθμών που είναι λύσεις του συστήματος
που είναι λύσεις του συστήματος

Λύση:
Θέτουμε και η πρώτη εξίσωση του συστήματος γίνεται
και η πρώτη εξίσωση του συστήματος γίνεται


Παρατηρούμε ότι αν τότε θα πρέπει και
τότε θα πρέπει και  . Άρα δεν υπάρχει λύση σε αυτή την περίπτωση.
. Άρα δεν υπάρχει λύση σε αυτή την περίπτωση.
Αν τώρα , έχουμε
, έχουμε



Άρα και η δεύτερη εξίσωση του συστήματος γίνεται
και η δεύτερη εξίσωση του συστήματος γίνεται
 . Τελικά οι λύσεις του συστήματος είναι οι τριάδες
. Τελικά οι λύσεις του συστήματος είναι οι τριάδες  και
και  .
.
Πρόβλημα 1
Να βρείτε όλες τις τριάδες πραγματικών αριθμών
 που είναι λύσεις του συστήματος
που είναι λύσεις του συστήματος 
Λύση:
Θέτουμε
 και η πρώτη εξίσωση του συστήματος γίνεται
και η πρώτη εξίσωση του συστήματος γίνεται

Παρατηρούμε ότι αν
 τότε θα πρέπει και
τότε θα πρέπει και  . Άρα δεν υπάρχει λύση σε αυτή την περίπτωση.
. Άρα δεν υπάρχει λύση σε αυτή την περίπτωση.Αν τώρα
 , έχουμε
, έχουμε


Άρα
 και η δεύτερη εξίσωση του συστήματος γίνεται
και η δεύτερη εξίσωση του συστήματος γίνεται . Τελικά οι λύσεις του συστήματος είναι οι τριάδες
. Τελικά οι λύσεις του συστήματος είναι οι τριάδες  και
και  .
.-
Xriiiiistos
- Δημοσιεύσεις: 219
- Εγγραφή: Τρί Μάιος 15, 2018 4:36 pm
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Ελπίζω να μην έχω κάνει λάθος θέμα 1ο των μεγάλων
Έχει λάθος η λύση
 προσθέτοντάς τα όλα έχουμε
προσθέτοντάς τα όλα έχουμε 
οπότε Αφού
Αφού  ΈΧΟΥΜΕ
ΈΧΟΥΜΕ  οπότε
οπότε  δεν διαιρεί το
δεν διαιρεί το  αλλά το 2 το διαιρεί αυτό σημαίνει πως το 2 δεν διαιρεί το
αλλά το 2 το διαιρεί αυτό σημαίνει πως το 2 δεν διαιρεί το  οπότε ο μεγαλύτερος εκθέτης που μπορούμε να υψώσουμε στο
οπότε ο μεγαλύτερος εκθέτης που μπορούμε να υψώσουμε στο  ΓΙΑ ΝΑ διαιρεί το
ΓΙΑ ΝΑ διαιρεί το  είναι το
είναι το 
Μετά από την πρώτη φορά που πέρνουμε τον τύπο για πολλαπλασιάζουμε τον τύπο για
πολλαπλασιάζουμε τον τύπο για  ώστε όταν τα προσθέσουμε αν απλοποιηθούν τα
ώστε όταν τα προσθέσουμε αν απλοποιηθούν τα  και αυτό το συνεχίζουμε μέχρι να φτάσουμε στο
και αυτό το συνεχίζουμε μέχρι να φτάσουμε στο 
Έχει λάθος η λύση
 προσθέτοντάς τα όλα έχουμε
προσθέτοντάς τα όλα έχουμε 
οπότε
 Αφού
Αφού  ΈΧΟΥΜΕ
ΈΧΟΥΜΕ  οπότε
οπότε  δεν διαιρεί το
δεν διαιρεί το  αλλά το 2 το διαιρεί αυτό σημαίνει πως το 2 δεν διαιρεί το
αλλά το 2 το διαιρεί αυτό σημαίνει πως το 2 δεν διαιρεί το  οπότε ο μεγαλύτερος εκθέτης που μπορούμε να υψώσουμε στο
οπότε ο μεγαλύτερος εκθέτης που μπορούμε να υψώσουμε στο  ΓΙΑ ΝΑ διαιρεί το
ΓΙΑ ΝΑ διαιρεί το  είναι το
είναι το 
Μετά από την πρώτη φορά που πέρνουμε τον τύπο για
 πολλαπλασιάζουμε τον τύπο για
πολλαπλασιάζουμε τον τύπο για  ώστε όταν τα προσθέσουμε αν απλοποιηθούν τα
ώστε όταν τα προσθέσουμε αν απλοποιηθούν τα  και αυτό το συνεχίζουμε μέχρι να φτάσουμε στο
και αυτό το συνεχίζουμε μέχρι να φτάσουμε στο 
τελευταία επεξεργασία από Xriiiiistos σε Σάβ Φεβ 23, 2019 3:29 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Ο γενικός όρος δεν είναι αυτός.Xriiiiistos έγραψε: ↑Σάβ Φεβ 23, 2019 2:37 pmΕλπίζω να μην έχω κάνει λάθος θέμα 1ο των μεγάλων
προσθέτοντάς τα όλα έχουμε
οπότεΑφού
ΈΧΟΥΜΕ
οπότε
δεν διαιρεί το
αλλά το 2 το διαιρεί αυτό σημαίνει πως το 2 δεν διαιρεί το
οπότε ο μεγαλύτερος εκθέτης που μπορούμε να υψώσουμε στο
ΓΙΑ ΝΑ διαιρεί το
είναι το

Είναι

-
Marlena Panagiotakou
- Δημοσιεύσεις: 2
- Εγγραφή: Σάβ Φεβ 23, 2019 2:41 pm
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Για το πρώτο θέμα στον Αρχιμήδη των μικρών τάξεων, η λύση που έγραψα:
Λύση:


 και
και 
άρα:




 ή
ή  άρα οι τριάδες είναι :
άρα οι τριάδες είναι : 

Λύση:


 και
και 
άρα:




 ή
ή  άρα οι τριάδες είναι :
άρα οι τριάδες είναι : 

- emouroukos
- Συντονιστής
- Δημοσιεύσεις: 1447
- Εγγραφή: Δευ Δεκ 22, 2008 1:27 pm
- Τοποθεσία: Αγρίνιο
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Πρόβλημα 1 Μεγάλων
Για κάθε είναι
είναι

Με πρόσθεση των σχέσεων αυτών κατά μέλη για και διαγράφοντας τους κοινούς όρους στα δύο μέλη, προκύπτει ότι
και διαγράφοντας τους κοινούς όρους στα δύο μέλη, προκύπτει ότι

Για κάθε θετικό ακέραιο είναι
είναι

Επειδή για κάθε ακέραιο ισχύει
ισχύει 
αν είναι η μεγαλύτερη δύναμη του
είναι η μεγαλύτερη δύναμη του  που διαιρεί τον
που διαιρεί τον  , θα είναι
, θα είναι  για κάθε ακέραιο
για κάθε ακέραιο 
Έτσι, αφού βρίσκουμε ότι
βρίσκουμε ότι  και άρα
και άρα 
Για κάθε
 είναι
είναι
Με πρόσθεση των σχέσεων αυτών κατά μέλη για
 και διαγράφοντας τους κοινούς όρους στα δύο μέλη, προκύπτει ότι
και διαγράφοντας τους κοινούς όρους στα δύο μέλη, προκύπτει ότι
Για κάθε θετικό ακέραιο
 είναι
είναι
Επειδή για κάθε ακέραιο
 ισχύει
ισχύει 
αν
 είναι η μεγαλύτερη δύναμη του
είναι η μεγαλύτερη δύναμη του  που διαιρεί τον
που διαιρεί τον  , θα είναι
, θα είναι  για κάθε ακέραιο
για κάθε ακέραιο 
Έτσι, αφού
 βρίσκουμε ότι
βρίσκουμε ότι  και άρα
και άρα 
Βαγγέλης Μουρούκος
Erro ergo sum.
Erro ergo sum.
- Al.Koutsouridis
- Δημοσιεύσεις: 1797
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Θέματα μικρών τάξεων
Πρόβλημα 2.
Λύση:
Έχουμε γιατί βαίνουν στο ίδιο τόξο. Ομοίως
γιατί βαίνουν στο ίδιο τόξο. Ομοίως  . Η
. Η  είναι μεσοκάθετος άρα και διχοτόμος της γωνίας
είναι μεσοκάθετος άρα και διχοτόμος της γωνίας  του τριγώνου
του τριγώνου  . Οπότε θα ισχύει
. Οπότε θα ισχύει  και επακόλουθα όλες οι παραπάνω γωνίες είναι ίσες μεταξύ τους.
και επακόλουθα όλες οι παραπάνω γωνίες είναι ίσες μεταξύ τους.
Επίσης ισχύει λόγω του εγγράψιμου τετραπλεύρου
λόγω του εγγράψιμου τετραπλεύρου  .
.
Από τις παραπάνω ισότητες γωνιών συμπεράνουμε ότι τα τρίγωνα είναι όμοια και εφόσον
είναι όμοια και εφόσον  , ορθογώνια.
, ορθογώνια.
Άρα θα είναι και τα σημεία
και τα σημεία  ομοκυκλικά.
ομοκυκλικά.
Πρόβλημα 2.
Λύση:
Έχουμε
 γιατί βαίνουν στο ίδιο τόξο. Ομοίως
γιατί βαίνουν στο ίδιο τόξο. Ομοίως  . Η
. Η  είναι μεσοκάθετος άρα και διχοτόμος της γωνίας
είναι μεσοκάθετος άρα και διχοτόμος της γωνίας  του τριγώνου
του τριγώνου  . Οπότε θα ισχύει
. Οπότε θα ισχύει  και επακόλουθα όλες οι παραπάνω γωνίες είναι ίσες μεταξύ τους.
και επακόλουθα όλες οι παραπάνω γωνίες είναι ίσες μεταξύ τους.Επίσης ισχύει
 λόγω του εγγράψιμου τετραπλεύρου
λόγω του εγγράψιμου τετραπλεύρου  .
. Από τις παραπάνω ισότητες γωνιών συμπεράνουμε ότι τα τρίγωνα
 είναι όμοια και εφόσον
είναι όμοια και εφόσον  , ορθογώνια.
, ορθογώνια.Άρα θα είναι
 και τα σημεία
και τα σημεία  ομοκυκλικά.
ομοκυκλικά.-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
https://en.wikipedia.org/wiki/Recurrence_relation
Η απόδειξη του τύπου είναι στάνταρ.
Η
έχει γενική λύση την
ενω μια λύση της μή ομογενους
δοκιμάζοντας είναι η
Αρα
Από την έχουμε
έχουμε  κλπ
κλπ
Η απόδειξη του τύπου είναι στάνταρ.
Η

έχει γενική λύση την

ενω μια λύση της μή ομογενους

δοκιμάζοντας είναι η

Αρα

Από την
 έχουμε
έχουμε  κλπ
κλπRe: ΑΡΧΙΜΗΔΗΣ 2018-2019
Για το  των μικρών. Σε καμία περίπτωση δεν γίνεται οι
των μικρών. Σε καμία περίπτωση δεν γίνεται οι  ,
,  να είναι και οι δύο πολλαπλάσια των
να είναι και οι δύο πολλαπλάσια των  εκτός αν
εκτός αν  . Συνεπώς, πάντα θα υπάρχει κάποιος που δεν διαιρείται με το
. Συνεπώς, πάντα θα υπάρχει κάποιος που δεν διαιρείται με το  , αφού αν wlog
, αφού αν wlog  ο τελευταίος που δεν διαιρείται από αυτό τότε θα επιλεχθεί μαζί με πολλαπλάσιο του
ο τελευταίος που δεν διαιρείται από αυτό τότε θα επιλεχθεί μαζί με πολλαπλάσιο του  και άρα κάποιος από τους δύο θα εξακολουθεί να μην διαιρείται με το
και άρα κάποιος από τους δύο θα εξακολουθεί να μην διαιρείται με το  .
.
 των μικρών. Σε καμία περίπτωση δεν γίνεται οι
των μικρών. Σε καμία περίπτωση δεν γίνεται οι  ,
,  να είναι και οι δύο πολλαπλάσια των
να είναι και οι δύο πολλαπλάσια των  εκτός αν
εκτός αν  . Συνεπώς, πάντα θα υπάρχει κάποιος που δεν διαιρείται με το
. Συνεπώς, πάντα θα υπάρχει κάποιος που δεν διαιρείται με το  , αφού αν wlog
, αφού αν wlog  ο τελευταίος που δεν διαιρείται από αυτό τότε θα επιλεχθεί μαζί με πολλαπλάσιο του
ο τελευταίος που δεν διαιρείται από αυτό τότε θα επιλεχθεί μαζί με πολλαπλάσιο του  και άρα κάποιος από τους δύο θα εξακολουθεί να μην διαιρείται με το
και άρα κάποιος από τους δύο θα εξακολουθεί να μην διαιρείται με το  .
.
τελευταία επεξεργασία από JimNt. σε Σάβ Φεβ 23, 2019 3:53 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Bye :')
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
-
socrates
- Επιμελητής
- Δημοσιεύσεις: 6461
- Εγγραφή: Δευ Μαρ 09, 2009 1:47 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Το πρόβλημα 3 των μικρών υπάρχει και εδώ (junior olympiad, θέμα 2):
https://drive.google.com/drive/folders/ ... 3YEwkASJSr
https://drive.google.com/drive/folders/ ... 3YEwkASJSr
Θανάσης Κοντογεώργης
- emouroukos
- Συντονιστής
- Δημοσιεύσεις: 1447
- Εγγραφή: Δευ Δεκ 22, 2008 1:27 pm
- Τοποθεσία: Αγρίνιο
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Πρόβλημα 3 Μεγάλων
Έστω και
και  όπου
όπου  θετικοί ακέραιοι με
θετικοί ακέραιοι με 
Είναι:


 .
.
Επειδή θα είναι και
θα είναι και 
Όμοια, αφού θα είναι και
θα είναι και 
Επομένως, από τη σχέση προκύπτει ότι
προκύπτει ότι  και
και 
Τότε, στη σχέση κάθε πρώτος παράγοντας των
κάθε πρώτος παράγοντας των  θα είναι υψωμένος σε εκθέτη
θα είναι υψωμένος σε εκθέτη  αντίστοιχα. Άρα, θα υπάρχει θετικός ακέραιος
αντίστοιχα. Άρα, θα υπάρχει θετικός ακέραιος  τέτοιος, ώστε
τέτοιος, ώστε  και
και 
Αν ήταν τότε θα είχαμε ότι
τότε θα είχαμε ότι  άτοπο. Άρα, είναι
άτοπο. Άρα, είναι  οπότε
οπότε 
Όμοια, υπάρχει θετικός ακέραιος τέτοιος, ώστε
τέτοιος, ώστε  και
και 
Τότε, είναι και
και 
Εύκολα ελέγχουμε ότι όλα τα ζεύγη με
με  θετικό ακέραιο, επαληθεύουν τη δοσμένη σχέση.
θετικό ακέραιο, επαληθεύουν τη δοσμένη σχέση.
Έστω
 και
και  όπου
όπου  θετικοί ακέραιοι με
θετικοί ακέραιοι με 
Είναι:


 .
.Επειδή
 θα είναι και
θα είναι και 
Όμοια, αφού
 θα είναι και
θα είναι και 
Επομένως, από τη σχέση
 προκύπτει ότι
προκύπτει ότι  και
και 
Τότε, στη σχέση
 κάθε πρώτος παράγοντας των
κάθε πρώτος παράγοντας των  θα είναι υψωμένος σε εκθέτη
θα είναι υψωμένος σε εκθέτη  αντίστοιχα. Άρα, θα υπάρχει θετικός ακέραιος
αντίστοιχα. Άρα, θα υπάρχει θετικός ακέραιος  τέτοιος, ώστε
τέτοιος, ώστε  και
και 
Αν ήταν
 τότε θα είχαμε ότι
τότε θα είχαμε ότι  άτοπο. Άρα, είναι
άτοπο. Άρα, είναι  οπότε
οπότε 
Όμοια, υπάρχει θετικός ακέραιος
 τέτοιος, ώστε
τέτοιος, ώστε  και
και 
Τότε, είναι
 και
και 
Εύκολα ελέγχουμε ότι όλα τα ζεύγη
 με
με  θετικό ακέραιο, επαληθεύουν τη δοσμένη σχέση.
θετικό ακέραιο, επαληθεύουν τη δοσμένη σχέση.Βαγγέλης Μουρούκος
Erro ergo sum.
Erro ergo sum.
-
Prødigy
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Και προφανώς πρέπειJimNt. έγραψε: ↑Σάβ Φεβ 23, 2019 3:28 pmΓια τοτων μικρών. Σε καμία περίπτωση δεν γίνεται οι
,
να είναι και οι δύο πολλαπλάσια των
εκτός αν
. Συνεπώς, πάντα θα υπάρχει κάποιος που δεν διαιρείται με το
, αφού αν wlog
ο τελευταίος που δεν διαιρείται από αυτό τότε θα επιλεχθεί μαζί με πολλαπλάσιο του
και άρα κάποιος από τους δύο θα εξακολουθεί να μην διαιρείται με το
.
 γιατί αλλιώς προκύπτει αρνητικός.
γιατί αλλιώς προκύπτει αρνητικός.Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Δεν έχει σημασία αυτό. Μου έκανε εντύπωση που επέλεξαν τοPrødigy έγραψε: ↑Σάβ Φεβ 23, 2019 4:05 pmΚαι προφανώς πρέπειJimNt. έγραψε: ↑Σάβ Φεβ 23, 2019 3:28 pmΓια τοτων μικρών. Σε καμία περίπτωση δεν γίνεται οι
,
να είναι και οι δύο πολλαπλάσια των
εκτός αν
. Συνεπώς, πάντα θα υπάρχει κάποιος που δεν διαιρείται με το
, αφού αν wlog
ο τελευταίος που δεν διαιρείται από αυτό τότε θα επιλεχθεί μαζί με πολλαπλάσιο του
και άρα κάποιος από τους δύο θα εξακολουθεί να μην διαιρείται με το
.
γιατί αλλιώς προκύπτει αρνητικός.
 αντι του
αντι του 
Bye :')
- Ανδρέας Πούλος
- Δημοσιεύσεις: 1494
- Εγγραφή: Κυρ Μαρ 01, 2009 10:47 pm
- Τοποθεσία: ΘΕΣΣΑΛΟΝΙΚΗ
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Θέμα Γεωμετρίας μικρών.
Το όνομα του κέντρου του περιγεγραμμένου κύκλου στο τετράπλευρο ΑΒΓΔ είναι περιττό.
Επίσης, υπάρχει λύση χωρίς καμία αναφορά στην καθετότητα.
Στο συνημμένο σχήμα πρέπει να αποδείξουμε ότι γωνία φ = Γ1 + Γ2 + Γ3, επειδή το τετράπλευρο ΑΒΓΔ είναι ήδη εγγεγραμμένο.
Όμως, φ = Γ2 + Γ3 + ΛΘΓ ως εξωτερική γωνία του τριγώνου ΛΘΓ.
Άρα, μένει να αποδείξουμε ότι Γ1 = ΛΘΓ.
Αυτό είναι πολύ απλό και φαίνεται στο συνημμένο σχήμα, αφού πρόκειται για γωνίες που είναι εγγεγραμμένες στο ίδιο τόξο
και για γωνίες που σχηματίζει η διχοτόμος του ισοσκελούς τριγώνου ΒΖΓ.
Συγνώμην, δεν μπορώ να γράψω σε Tex με ελληνικά γράμματα και να κάνω το σχήμα μικρότερο.
Το όνομα του κέντρου του περιγεγραμμένου κύκλου στο τετράπλευρο ΑΒΓΔ είναι περιττό.
Επίσης, υπάρχει λύση χωρίς καμία αναφορά στην καθετότητα.
Στο συνημμένο σχήμα πρέπει να αποδείξουμε ότι γωνία φ = Γ1 + Γ2 + Γ3, επειδή το τετράπλευρο ΑΒΓΔ είναι ήδη εγγεγραμμένο.
Όμως, φ = Γ2 + Γ3 + ΛΘΓ ως εξωτερική γωνία του τριγώνου ΛΘΓ.
Άρα, μένει να αποδείξουμε ότι Γ1 = ΛΘΓ.
Αυτό είναι πολύ απλό και φαίνεται στο συνημμένο σχήμα, αφού πρόκειται για γωνίες που είναι εγγεγραμμένες στο ίδιο τόξο
και για γωνίες που σχηματίζει η διχοτόμος του ισοσκελούς τριγώνου ΒΖΓ.
Συγνώμην, δεν μπορώ να γράψω σε Tex με ελληνικά γράμματα και να κάνω το σχήμα μικρότερο.
- emouroukos
- Συντονιστής
- Δημοσιεύσεις: 1447
- Εγγραφή: Δευ Δεκ 22, 2008 1:27 pm
- Τοποθεσία: Αγρίνιο
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Πρόβλημα 2 Μεγάλων
Το σχήμα - και η απόδειξη (χωρίς λέξεις).
Το σχήμα - και η απόδειξη (χωρίς λέξεις).
Βαγγέλης Μουρούκος
Erro ergo sum.
Erro ergo sum.
-
Κώστας Καρ.
- Δημοσιεύσεις: 7
- Εγγραφή: Πέμ Ιαν 24, 2019 10:17 pm
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Καλησπέρα
Για το θέμα 4 των μεγαλων εγραψα αυτο:
Στο υπολοιπο της ασκησης θα θεωρω μ της στηλες και ν τις γραμμες του ορθογωνιου
Παρατηρούμε οτι, συμφωνα με την επιτρεπομενη κινηση, καθε στηλη και καθε γραμμη πρεπει να.περιεχει τουλαχιστον ενα αρχικό μαυρο πιόνι, αλλιως δεν μπορει να γεμισει. Ετσι, αν ειναι , τοτε εχουμε τετραγωνο με
, τοτε εχουμε τετραγωνο με
 μοναδιαια τετραγωνα. Τοτε προφανώς η μικρότερη δυνατη τιμη αρχικών μαυρων πιονων ειναι τα μοναδιαια τετραγωνα της διαγωνιου, δηλαδη
μοναδιαια τετραγωνα. Τοτε προφανώς η μικρότερη δυνατη τιμη αρχικών μαυρων πιονων ειναι τα μοναδιαια τετραγωνα της διαγωνιου, δηλαδη 
Αν , τοτε χωριζουμε το ορθογωνιο σε ενα τετραγωνο με πλευρες
, τοτε χωριζουμε το ορθογωνιο σε ενα τετραγωνο με πλευρες  και ενα ορθογωνιο με πλευρες
και ενα ορθογωνιο με πλευρες  και και
και και  (αν
(αν  , τοτε προφανώς δεν ειναι ορθογώνιο αλλα τετραγωνο με επισης πλευρες
, τοτε προφανώς δεν ειναι ορθογώνιο αλλα τετραγωνο με επισης πλευρες  ). Εφοσον τωρα για να γεμισουμε το τετραγωνο με πλευρες ν θελουμε ν αρχικα πιονια, επειδη η πλευρα διπλα απ'το ορθογωνιο (δηλαδη η ακριανη στηλη του τετραγωνου) θα ειναι γεματη με μαυρα πιονια, παρατηρουμε οτι χρειαζομαστε μόνο ενα αρχικο μαυρο πιόνι σε καθε στηλη για να γεμισουμε το ορθογωνιο, ανεξαρτητα απ'την θεση τους. Δηλαδη χρειαζομαστε αλλα
). Εφοσον τωρα για να γεμισουμε το τετραγωνο με πλευρες ν θελουμε ν αρχικα πιονια, επειδη η πλευρα διπλα απ'το ορθογωνιο (δηλαδη η ακριανη στηλη του τετραγωνου) θα ειναι γεματη με μαυρα πιονια, παρατηρουμε οτι χρειαζομαστε μόνο ενα αρχικο μαυρο πιόνι σε καθε στηλη για να γεμισουμε το ορθογωνιο, ανεξαρτητα απ'την θεση τους. Δηλαδη χρειαζομαστε αλλα  αρχικα τετραγωνα.
αρχικα τετραγωνα.
Αρα στο συνολο έχουμε:

Με συγχωρείτε για την απουσια σχηματος αλλα αυτο το γραφω μεσω κινητου γιατι βρισκομαι στον δρομο της επιστροφης. Πως σας φανηκε η λυση μου;
Για το θέμα 4 των μεγαλων εγραψα αυτο:
Στο υπολοιπο της ασκησης θα θεωρω μ της στηλες και ν τις γραμμες του ορθογωνιου
Παρατηρούμε οτι, συμφωνα με την επιτρεπομενη κινηση, καθε στηλη και καθε γραμμη πρεπει να.περιεχει τουλαχιστον ενα αρχικό μαυρο πιόνι, αλλιως δεν μπορει να γεμισει. Ετσι, αν ειναι
 , τοτε εχουμε τετραγωνο με
, τοτε εχουμε τετραγωνο με  μοναδιαια τετραγωνα. Τοτε προφανώς η μικρότερη δυνατη τιμη αρχικών μαυρων πιονων ειναι τα μοναδιαια τετραγωνα της διαγωνιου, δηλαδη
μοναδιαια τετραγωνα. Τοτε προφανώς η μικρότερη δυνατη τιμη αρχικών μαυρων πιονων ειναι τα μοναδιαια τετραγωνα της διαγωνιου, δηλαδη 
Αν
 , τοτε χωριζουμε το ορθογωνιο σε ενα τετραγωνο με πλευρες
, τοτε χωριζουμε το ορθογωνιο σε ενα τετραγωνο με πλευρες  και ενα ορθογωνιο με πλευρες
και ενα ορθογωνιο με πλευρες  και και
και και  (αν
(αν  , τοτε προφανώς δεν ειναι ορθογώνιο αλλα τετραγωνο με επισης πλευρες
, τοτε προφανώς δεν ειναι ορθογώνιο αλλα τετραγωνο με επισης πλευρες  ). Εφοσον τωρα για να γεμισουμε το τετραγωνο με πλευρες ν θελουμε ν αρχικα πιονια, επειδη η πλευρα διπλα απ'το ορθογωνιο (δηλαδη η ακριανη στηλη του τετραγωνου) θα ειναι γεματη με μαυρα πιονια, παρατηρουμε οτι χρειαζομαστε μόνο ενα αρχικο μαυρο πιόνι σε καθε στηλη για να γεμισουμε το ορθογωνιο, ανεξαρτητα απ'την θεση τους. Δηλαδη χρειαζομαστε αλλα
). Εφοσον τωρα για να γεμισουμε το τετραγωνο με πλευρες ν θελουμε ν αρχικα πιονια, επειδη η πλευρα διπλα απ'το ορθογωνιο (δηλαδη η ακριανη στηλη του τετραγωνου) θα ειναι γεματη με μαυρα πιονια, παρατηρουμε οτι χρειαζομαστε μόνο ενα αρχικο μαυρο πιόνι σε καθε στηλη για να γεμισουμε το ορθογωνιο, ανεξαρτητα απ'την θεση τους. Δηλαδη χρειαζομαστε αλλα  αρχικα τετραγωνα.
αρχικα τετραγωνα. Αρα στο συνολο έχουμε:

Με συγχωρείτε για την απουσια σχηματος αλλα αυτο το γραφω μεσω κινητου γιατι βρισκομαι στον δρομο της επιστροφης. Πως σας φανηκε η λυση μου;
τελευταία επεξεργασία από Demetres σε Σάβ Φεβ 23, 2019 8:48 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λόγος: Γραφή σε LaTeX
Λόγος: Γραφή σε LaTeX
Re: ΑΡΧΙΜΗΔΗΣ 2018-2019
Καλησπέρα. Σε αυτού του είδους τα προβλήματα πρέπει να δείξουμε δύο πράγματα.Κώστας Καρ. έγραψε: ↑Σάβ Φεβ 23, 2019 5:05 pmΚαλησπέρα
Για το θέμα 4 των μεγαλων εγραψα αυτο:
Στο υπολοιπο της ασκησης θα θεωρω μ της στηλες και ν τις γραμμες του ορθογωνιου
Παρατηρούμε οτι, συμφωνα με την επιτρεπομενη κινηση, καθε στηλη και καθε γραμμη πρεπει να.περιεχει τουλαχιστον ενα αρχικό μαυρο πιόνι, αλλιως δεν μπορει να γεμισει. Ετσι, αν ειναι ν=μ, τοτε εχουμε τετραγωνο με
ν^2 μοναδιαια τετραγωνα. Τοτε προφανώς η μικρότερη δυνατη τιμη αρχικών μαυρων πιονων ειναι τα μοναδιαια τετραγωνα της διαγωνιου, δηλαδη Ν=ν
Αν ν<μ, τοτε χωριζουμε το ορθογωνιο σε ενα τετραγωνο με πλευρες ν και ενα ορθογωνιο με πλευρες μ-ν και και ν (αν μ=2ν, τοτε προφανώς δεν ειναι ορθογώνιο αλλα τετραγωνο με επισης πλευρες ν). Εφοσον τωρα για να γεμισουμε το τετραγωνο με πλευρες ν θελουμε ν αρχικα πιονια, επειδη η πλευρα διπλα απ'το ορθογωνιο (δηλαδη η ακριανη στηλη του τετραγωνου) θα ειναι γεματη με μαυρα πιονια, παρατηρουμε οτι χρειαζομαστε μόνο ενα αρχικο μαυρο πιόνι σε καθε στηλη για να γεμισουμε το ορθογωνιο, ανεξαρτητα απ'την θεση τους. Δηλαδη χρειαζομαστε αλλα μ-ν αρχικα τετραγωνα.
Αρα στο συνολο έχουμε:
Ν=ν+(μ-ν)=μ
Με συγχωρείτε για την απουσια σχηματος αλλα αυτο το γραφω μεσω κινητου γιατι βρισκομαι στον δρομο της επιστροφης. Πως σας φανηκε η λυση μου;
1ον) Ότι χρειάζονται τουλάχιστον τόσα μαύρα τετράγωνα
2ον) Ότι με τον αριθμό που βρήκαμε πριν είναι δυνατόν.
Εσύ κάνεις ουσιαστικά μόνο το 2ο κομμάτι. Η απάντηση για το τετράγωνο είναι σωστή, αλλά για το ορθογώνιο είναι λάθος.
Σιλουανός Μπραζιτίκος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
