1) Κατ' αρχήν, το σχολικό βιβλίο εξυπηρέτησε μιαν ανάγκη, αλλά δεν είναι και το καλύτερο εγχειρίδιο διαφορικού λογισμού.
2) Ας διευκρινίσουμε, επίσης, ότι από βιβλίο σε βιβλίο -συγγραφέα σε συγγραφέα- υπάρχουν κάποιες διαφορές για το πότε ορίζεται κατακόρυφη εφαπτομένη, αλλά αυτό δεν προκαλεί σύγχυση, αφού κάθε συγγραφέας ξεκαθαρίζει -σε κάποιο σημείο- το συγκεκριμένο θέμα.
3) Αν θέλουμε να μιλήσουμε για την κλίση της εφαπτομένης ευθείας, είναι προτιμότερο να χρησιμοποιήσουμε το όριο

, αντί την εφαπτομένη της γωνίας

που σχηματίζει η εφαπτομένη ευθεία με τον θετικό ημιάξονα των

.
Ως γνωστόν, αν το

υπάρχει και είναι πραγματικός αριθμός, αυτό ονομάζεται παράγωγος της

στο

και, τότε, ισούται με την

.
Αν

ή

, τότε η κάθετη ευθεία

μπορεί να θεωρηθεί ως εφαπτομένη ευθεία στην

, αλλά με αρκετούς αστερίσκους. π.χ. τι θεωρούμε όταν

και

; ή όταν

και

; και όταν στην δεύτερη περίπτωση, η συνάρτηση είναι ακόμα και ασυνεχής στο

;
Όπως έγραψε και ο Λάμπρος παραπάνω αλλά και ο ίδιος: Είναι θέμα συμφωνίας, αλλά αυτό δεν μπερδεύει το συγκεκριμένο θέμα.
 (με f συνεχής), έχουμε κατακόρυφη εφαπτομένη την
(με f συνεχής), έχουμε κατακόρυφη εφαπτομένη την  .Τότε ισχύει ότι
.Τότε ισχύει ότι  άρα και ο συντελεστής διεύθυνσης της εφαπτομένης μας είναι
άρα και ο συντελεστής διεύθυνσης της εφαπτομένης μας είναι  .Λέμε όμως από το λύκειο ότι ο συντελεστής διεύθυνσης μίας κατακόρυφης ευθείας δεν ορίζεται.Πως λοιπόν εξηγείται το παραπάνω.Δεν ορίζεται ή ισούται με άπειρο?Έχω χαθεί λιγάκι....
.Λέμε όμως από το λύκειο ότι ο συντελεστής διεύθυνσης μίας κατακόρυφης ευθείας δεν ορίζεται.Πως λοιπόν εξηγείται το παραπάνω.Δεν ορίζεται ή ισούται με άπειρο?Έχω χαθεί λιγάκι....
 δεν ορίζεται, δεν λέμε ότι ο συντελεστής διεύθυνσης της εφαπτομένης στο
δεν ορίζεται, δεν λέμε ότι ο συντελεστής διεύθυνσης της εφαπτομένης στο  , όταν αυτή είναι κατακόρυφη, είναι
, όταν αυτή είναι κατακόρυφη, είναι 

 Εικάζω ότι ο συγγραφέας στο βιβλίο που αναφέρεσε δουλεύει στο επεκτεταμένο σύνολο των πραγματικών σε αντίθεση με το σχολικό.
Εικάζω ότι ο συγγραφέας στο βιβλίο που αναφέρεσε δουλεύει στο επεκτεταμένο σύνολο των πραγματικών σε αντίθεση με το σχολικό. , αντί την εφαπτομένη της γωνίας
, αντί την εφαπτομένη της γωνίας  που σχηματίζει η εφαπτομένη ευθεία με τον θετικό ημιάξονα των
που σχηματίζει η εφαπτομένη ευθεία με τον θετικό ημιάξονα των  .
.  στο
στο  και, τότε, ισούται με την
και, τότε, ισούται με την  .
. ή
ή  , τότε η κάθετη ευθεία
, τότε η κάθετη ευθεία  μπορεί να θεωρηθεί ως εφαπτομένη ευθεία στην
μπορεί να θεωρηθεί ως εφαπτομένη ευθεία στην  , αλλά με αρκετούς αστερίσκους. π.χ. τι θεωρούμε όταν
, αλλά με αρκετούς αστερίσκους. π.χ. τι θεωρούμε όταν  και
και  ; ή όταν
; ή όταν  και
και  ; και όταν στην δεύτερη περίπτωση, η συνάρτηση είναι ακόμα και ασυνεχής στο
; και όταν στην δεύτερη περίπτωση, η συνάρτηση είναι ακόμα και ασυνεχής στο 
 .Ο συντελεστής σε αυτήν την περίπτωση που κουβεντιάζουμε δεν ορίζεται.Είναι
.Ο συντελεστής σε αυτήν την περίπτωση που κουβεντιάζουμε δεν ορίζεται.Είναι  .Επομένως η κλίση δεν ορίζεται μεν, αλλά επειδή το όριο της ισούται με άπειρο λέμε και ότι "η κλίση είναι άπειρη".Κάπως έτσι το εννοείτε?
.Επομένως η κλίση δεν ορίζεται μεν, αλλά επειδή το όριο της ισούται με άπειρο λέμε και ότι "η κλίση είναι άπειρη".Κάπως έτσι το εννοείτε? .
.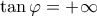 είναι λάθος.(Απειροστικος Λογισμος Ι,Σωτήρη Κ. Ντούγια σελ. 316)
είναι λάθος.(Απειροστικος Λογισμος Ι,Σωτήρη Κ. Ντούγια σελ. 316) . (Το ίδιο και για τις πλευρικές παραγώγους.)
. (Το ίδιο και για τις πλευρικές παραγώγους.) ?
? . Πάντως, ο κ. Ντούγιας χρησιμοποιεί αυτόν τον συμβολισμό (περίπτωση) για να εισάγει στην αμέσως επόμενη σελίδα (αναφέροντας αυτήν την περίπτωση) την έννοια της "κατ' εκδοχήν παραγώγου". Μαθηματικά, αυτό είναι θεμιτό.
. Πάντως, ο κ. Ντούγιας χρησιμοποιεί αυτόν τον συμβολισμό (περίπτωση) για να εισάγει στην αμέσως επόμενη σελίδα (αναφέροντας αυτήν την περίπτωση) την έννοια της "κατ' εκδοχήν παραγώγου". Μαθηματικά, αυτό είναι θεμιτό.