 , είναι
, είναι  και
και  το μέσο της υποτείνουσας
το μέσο της υποτείνουσας  .
.Στην προέκταση της
 , θεωρούμε σημείο
, θεωρούμε σημείο  και φέρουμε την
και φέρουμε την  , η οποία τέμνει την
, η οποία τέμνει την 
στο σημείο
 . Η κάθετη
. Η κάθετη 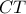 από το
από το  προς την
προς την  , προεκτεινόμενη τέμνει την
, προεκτεινόμενη τέμνει την  στο σημείο
στο σημείο  .
.Βρείτε την θέση του
 για την οποία μεγιστοποιείται το
για την οποία μεγιστοποιείται το 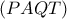 και υπολογίστε το
και υπολογίστε το  .
.
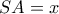
 με διατέμνουσα
με διατέμνουσα  :
: 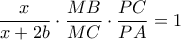



 :
: 
 και έχουμε :
και έχουμε :


 που ισχύει ,με την ισότητα για
που ισχύει ,με την ισότητα για  .
.
 το μέσο του
το μέσο του  . Σχηματίζω το τετράγωνο
. Σχηματίζω το τετράγωνο 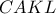 . Προφανώς :
. Προφανώς : 
 με
με  . Θα ισχύουν :
. Θα ισχύουν :
 και λόγω των
και λόγω των  θα έχω:
θα έχω: 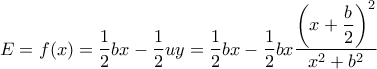 ή
ή 
 , το εμβαδόν θα παίρνει μέγιστη τιμή :
, το εμβαδόν θα παίρνει μέγιστη τιμή : όταν
όταν  .
.
 . Το
. Το 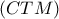 είναι ορθογώνιο τρίγωνο με σταθερή υποτείνουσα
είναι ορθογώνιο τρίγωνο με σταθερή υποτείνουσα 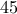 ως προς την
ως προς την  .
.