Μια από τις εκδόσεις των θεμάτων για το 2019.
1. Ένας φοιτητής έγραψε πρόγραμμα που επαναχρωματίζει το πίξελ σε ένα από
 διαφορετικά χρώματα. Τα χρώματα αυτά είναι αριθμημένα με φυσικούς αριθμούς από το
διαφορετικά χρώματα. Τα χρώματα αυτά είναι αριθμημένα με φυσικούς αριθμούς από το  έως το
έως το  , εξάλλου τα βασικά χρώματα έλαβαν τους ακόλουθους αριθμούς: το άσπρο χρώματα τον αριθμό
, εξάλλου τα βασικά χρώματα έλαβαν τους ακόλουθους αριθμούς: το άσπρο χρώματα τον αριθμό  , το κόκκινο -
, το κόκκινο - , το πορτοκαλί -
, το πορτοκαλί - , το κίτρινο-
, το κίτρινο- , το πράσινο -
, το πράσινο - , το γαλάζιο -
, το γαλάζιο - , το κυανό -
, το κυανό - , το μωβ -
, το μωβ - , το μαύρο -
, το μαύρο - . Αν το αρχικό χρώμα του πίξελ έχει αριθμό
. Αν το αρχικό χρώμα του πίξελ έχει αριθμό  , τότε το πρόγραμμα του φοιτητή το χρωματίζει σε χρώμα με αριθμό
, τότε το πρόγραμμα του φοιτητή το χρωματίζει σε χρώμα με αριθμό  και αν στο αρχικό χρώμα του πίξελ αντιστοιχεί αριθμός
και αν στο αρχικό χρώμα του πίξελ αντιστοιχεί αριθμός  , τότε το πίξελ χρωματίζεται με χρώμα που αντιστοιχεί στον αριθμό
, τότε το πίξελ χρωματίζεται με χρώμα που αντιστοιχεί στον αριθμό  . Αρχικά το πίξελ είχε κόκκινο χρώμα. Ο φοιτητής εφάρμοσε διαδοχικά το πρόγραμμα
. Αρχικά το πίξελ είχε κόκκινο χρώμα. Ο φοιτητής εφάρμοσε διαδοχικά το πρόγραμμα  φορές. Με ποιο χρώμα χρωματίστηκε το πίξελ στο τέλος; [12 μόρια]
φορές. Με ποιο χρώμα χρωματίστηκε το πίξελ στο τέλος; [12 μόρια]2. Να λύσετε την ανισότητα
![\displaystyle{ \sqrt{3} \tan x - \sqrt[4]{\sin y} - \sqrt{\dfrac{3}{\cos^2 x} +\sqrt{\sin y} - 6 } \geq \sqrt{3}} \displaystyle{ \sqrt{3} \tan x - \sqrt[4]{\sin y} - \sqrt{\dfrac{3}{\cos^2 x} +\sqrt{\sin y} - 6 } \geq \sqrt{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/1a2acc4393d805d31c3df9b3d6bec141.png) . [12 μόρια]
. [12 μόρια]3. Να βρείτε όλα τα ζεύγη θετικών ακεραίων
 και
και  , για τα οποία εκ των τεσσάρων ισχυρισμών
, για τα οποία εκ των τεσσάρων ισχυρισμών1)
 διαιρείται με το
διαιρείται με το 
2)

3)
 διαιρείται με το
διαιρείται με το 
4)
 είναι πρώτος αριθμός
είναι πρώτος αριθμόςτρεις είναι αληθείς και ένας ψευδής. [16 μόρια]
4. Στο τρίγωνο
 με την γωνία
με την γωνία  να είναι ίση με
να είναι ίση με  , φέρουμε την διχοτόμο
, φέρουμε την διχοτόμο  . Η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου
. Η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου  με κέντρο το σημείο
με κέντρο το σημείο  , είναι ίση με
, είναι ίση με  . Αν
. Αν  , vα βρείτε το μήκος του τμήματος
, vα βρείτε το μήκος του τμήματος  , όπου
, όπου  το σημείο τομής των τμημάτων
το σημείο τομής των τμημάτων  και
και  . [20 μόρια]
. [20 μόρια]5. Για κάθε τιμή της παραμέτρου
 να λύσετε την εξίσωση
να λύσετε την εξίσωση . [20 μόρια]
. [20 μόρια]6. Η βάση της πυραμίδας
 είναι το τρίγωνο
είναι το τρίγωνο  , όλες οι πλευρές του οποίου είναι ίσες με
, όλες οι πλευρές του οποίου είναι ίσες με  και το ύψος της συμπίπτει με την παράπλευρη ακμή
και το ύψος της συμπίπτει με την παράπλευρη ακμή  . Να βρείτε το εμβαδόν της τομής της πυραμίδας με το επίπεδο, που διέρχεται από το κέντρο της περιγεγραμμένης στην πυραμίδα σφαίρας, σχηματίζει γωνία
. Να βρείτε το εμβαδόν της τομής της πυραμίδας με το επίπεδο, που διέρχεται από το κέντρο της περιγεγραμμένης στην πυραμίδα σφαίρας, σχηματίζει γωνία  με την βάση, τέμνει την ακμή
με την βάση, τέμνει την ακμή  στο σημείο
στο σημείο  , ώστε
, ώστε  και τέμνει την ακμή
και τέμνει την ακμή  . Είναι γνωστό, ότι η απόσταση του σημείου
. Είναι γνωστό, ότι η απόσταση του σημείου  από το επίπεδο τομής είναι ίση με
από το επίπεδο τομής είναι ίση με 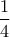 . [20 μόρια]
. [20 μόρια]

 και με τον τύπο της διχοτόμου
και με τον τύπο της διχοτόμου 
 Αλλά,
Αλλά, 
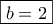



 .
.
 κατι το οποίο δεν το γνωρίζουμε ακόμη και το εξάγουμε δεδομένου ότι
κατι το οποίο δεν το γνωρίζουμε ακόμη και το εξάγουμε δεδομένου ότι  , αν καταλαβαίνω καλά.
, αν καταλαβαίνω καλά.

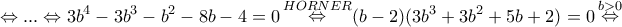
 Η συνέχεια όπως και πριν...
Η συνέχεια όπως και πριν...
![a=\sqrt{3}tanx,\,\,\,b=\sqrt[4]{siny} a=\sqrt{3}tanx,\,\,\,b=\sqrt[4]{siny}](/forum/ext/geomar/texintegr/latexrender/pictures/fdfee3bd15d37863dd4bcb3bf26a4b4c.png) . Επειδή
. Επειδή  η ανίσωση γράφεται τελικά
η ανίσωση γράφεται τελικά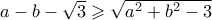

 , οπότε
, οπότε  . Έτσι
. Έτσι  .
.  άρα
άρα  κ.λπ.
κ.λπ. 
 το οποίο όμως έρχεται σε αντίφαση με την 4). Αρα μία εκ των 3), 4) είναι η ψευδής, άρα οι 1) και 2) είναι αληθείς.
το οποίο όμως έρχεται σε αντίφαση με την 4). Αρα μία εκ των 3), 4) είναι η ψευδής, άρα οι 1) και 2) είναι αληθείς. . Επειδή όμως
. Επειδή όμως![a,b> 0\Rightarrow 2b-a+4=0\Rightarrow a=2b+4....[5] a,b> 0\Rightarrow 2b-a+4=0\Rightarrow a=2b+4....[5]](/forum/ext/geomar/texintegr/latexrender/pictures/e0f7c1ab96edd449f8820161f3975117.png) .
.![[5] [5]](/forum/ext/geomar/texintegr/latexrender/pictures/7b98d2564df78c56a60805f6e8e11a86.png) στην
στην ![[3]\Rightarrow 4\left | 4b+5 [3]\Rightarrow 4\left | 4b+5](/forum/ext/geomar/texintegr/latexrender/pictures/d9e4f3a2e4c0f0a61dcf445af22e9fb9.png) που είναι ψευδής άρα η
που είναι ψευδής άρα η ![[4] [4]](/forum/ext/geomar/texintegr/latexrender/pictures/e962e23c139e7252904b9221d9967442.png) είναι αληθής.
είναι αληθής.![[1]\Rightarrow b\left |4b^{2}+24b+35\Rightarrow b\left |35\Rightarrow b\in \left \{ 1,5,7,35 \right \} [1]\Rightarrow b\left |4b^{2}+24b+35\Rightarrow b\left |35\Rightarrow b\in \left \{ 1,5,7,35 \right \}](/forum/ext/geomar/texintegr/latexrender/pictures/dbf9b74154de6664c919d03ad55c72e8.png) .
. επαληθεύουν την
επαληθεύουν την 
 όπου το τρίγωνο της βάσης είναι το ισόπλευρο τρίγωνο
όπου το τρίγωνο της βάσης είναι το ισόπλευρο τρίγωνο 


 είναι το κέντρο της περιγεγραμμένης στην πυραμίδα αυτή σφαίρας και συνεπώς το σημείο αυτό ισαπέχει από
είναι το κέντρο της περιγεγραμμένης στην πυραμίδα αυτή σφαίρας και συνεπώς το σημείο αυτό ισαπέχει από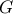 του ισοπλεύρου τριγώνου.
του ισοπλεύρου τριγώνου. είναι το μέσον της
είναι το μέσον της  τότε
τότε  μεσοκάθετος της
μεσοκάθετος της 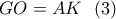
 είναι ένα σημείο της πλευράς
είναι ένα σημείο της πλευράς  και είναι:
και είναι: 

 , όπου τέτοια ώστε να σχηματίζει με
, όπου τέτοια ώστε να σχηματίζει με  και
και  τυχαίο σημείο αυτού.
τυχαίο σημείο αυτού. απόσταση
απόσταση 
 στο
στο  ενώ η κοινή του τομή
ενώ η κοινή του τομή  με το επίπεδο
με το επίπεδο  τέμνει την
τέμνει την  . (η
. (η  και το
και το  που θα ορίσουμε στη συνέχεια)
που θα ορίσουμε στη συνέχεια) κάθετο στην
κάθετο στην  έχει σαν ύψος το
έχει σαν ύψος το  και ακόμα
και ακόμα 
 και
και  , οπότε
, οπότε 

 . Αυτό σημαίνει ότι η ζητούμενη τομή είναι το τρίγωνο
. Αυτό σημαίνει ότι η ζητούμενη τομή είναι το τρίγωνο 
 το πλήθος των επαναλήψεων (μέχρι το
το πλήθος των επαναλήψεων (μέχρι το  ο κωδικός του χρώματος.
ο κωδικός του χρώματος. έχουμε εισέλθει σε ατέρμονα βρόχο μήκους
έχουμε εισέλθει σε ατέρμονα βρόχο μήκους  , όπου τα
, όπου τα  επαναλαμβάνονται συνεχώς με αυτή τη σειρά.
επαναλαμβάνονται συνεχώς με αυτή τη σειρά. . Αρα το χρώμα που θα εμφανιστεί στο τέλος είναι το κυανό.
. Αρα το χρώμα που θα εμφανιστεί στο τέλος είναι το κυανό. , αφού
, αφού 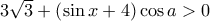 , και, η συνάρτηση
, και, η συνάρτηση  είναι 1-1.
είναι 1-1.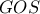 και
και  , τα οποία είναι ορθογώνια και
, τα οποία είναι ορθογώνια και  προς το ανωτέρω επίπεδο για το λόγο αυτό η γωνίες των
προς το ανωτέρω επίπεδο για το λόγο αυτό η γωνίες των  εκφράζουν τη γωνία του ζητούμενου επιπέδου με το επίπεδο της βάσης της δοθείσας πυραμίδας.
εκφράζουν τη γωνία του ζητούμενου επιπέδου με το επίπεδο της βάσης της δοθείσας πυραμίδας. και
και 
 έτσι είναι:
έτσι είναι: 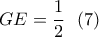 (η αρίθμηση είναι συνέχεια της προηγούμενης ανάρτησης)
(η αρίθμηση είναι συνέχεια της προηγούμενης ανάρτησης)
 προκύπτει:
προκύπτει: 

 (καθώς είναι τα
(καθώς είναι τα  του ύψους του ισοπλεύρου τριγώνου)
του ύψους του ισοπλεύρου τριγώνου)
 προκύπτει:
προκύπτει:
 δεχόμαστε προφανώς την
δεχόμαστε προφανώς την 
 . Άρα το ισόπλευρο τρίγωνο
. Άρα το ισόπλευρο τρίγωνο  (του σχήματος στην προηγούμενη ανάρτηση) έγιναν πλέον ίσα και με ακτίνα
(του σχήματος στην προηγούμενη ανάρτηση) έγιναν πλέον ίσα και με ακτίνα 
 των ίσων κύκλων
των ίσων κύκλων  και
και  με γνωστή την ακτίνα τους από την (13)
με γνωστή την ακτίνα τους από την (13)  , το σημείο
, το σημείο  επί της ακμής
επί της ακμής 
 γνωρίζουμε:
γνωρίζουμε:  (από την εκφώνηση του προβλήματος)
(από την εκφώνηση του προβλήματος) (διότι
(διότι  , αφού
, αφού  )
) (διότι
(διότι 
 .
. άρα τέμνει την
άρα τέμνει την 
 τέμνει την
τέμνει την  γιατί ως ευθείες του ιδίου επιπέδου αν δεν τέμνονταν θα ήταν παράλληλες. Όμως τότε η
γιατί ως ευθείες του ιδίου επιπέδου αν δεν τέμνονταν θα ήταν παράλληλες. Όμως τότε η  τέμνει την
τέμνει την 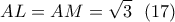 (καθόσον το τρίγωνο
(καθόσον το τρίγωνο  είναι ισοσκλελές)
είναι ισοσκλελές) το θεώρημα του Μενελάου με διατέμνουσα την
το θεώρημα του Μενελάου με διατέμνουσα την 
 της τομής του επιπέδου αυτού με την πυραμίδα.
της τομής του επιπέδου αυτού με την πυραμίδα.
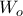 στην βάση της πυραμίδας
στην βάση της πυραμίδας 
 επομένως προβάλλεται στο τετράπλευρο
επομένως προβάλλεται στο τετράπλευρο 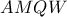 επί του επιπέδου της βάσης της πυραμίδας αυτής και
επί του επιπέδου της βάσης της πυραμίδας αυτής και 
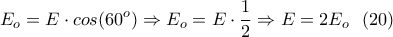


 (διότι MQ//AR και
(διότι MQ//AR και 

 (από την (19))
(από την (19))
