1) Να εξετασετε αν:
α) Υπαρχουν γνησια αυξουσες συναρτησεις f,g: R --> R, ωστε f(x) - g(x) = sinx σε ολο το R
β) Υπαρχουν γνησια αυξουσες συναρτησεις f,g: R --> (0, +
 ), ωστε f(x) - g(x) = sinx σε ολο το R
), ωστε f(x) - g(x) = sinx σε ολο το R2) Εστω πολυωνυμο
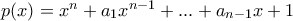 με θετικους συντελεστες και n πραγματικες ριζες, να δειχθει οτι:
με θετικους συντελεστες και n πραγματικες ριζες, να δειχθει οτι:α)
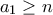 και
και 
β)
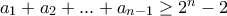 , ποτε ισχυει η ισοτητα?
, ποτε ισχυει η ισοτητα?γ)

3) Νδο
 , οταν
, οταν  ειναι συνεχως παραγωγισημη συναρτηση
ειναι συνεχως παραγωγισημη συναρτηση4) Για τους θετικους ακεραιους
 ισχυει
ισχυει  για καθε
για καθε  . Νδο υπαρχουν θετικοι ακεραιοι
. Νδο υπαρχουν θετικοι ακεραιοι  ωστε
ωστε 
5) Για εναν 2x2 πινακα A με στοιχεια ακεραιους αριθμους ισχυει
 .
.α) Να δειχθει οτι
 .
.β) Να βρεθουν οι δυνατες τιμες για τα
 .
.
 και
και  .
. , πρέπει
, πρέπει  και άρα
και άρα  . Είναι εύκολο τώρα να δειχθεί ότι η
. Είναι εύκολο τώρα να δειχθεί ότι η  δεν μπορεί να παίρνει μόνο θετικές τιμές.
δεν μπορεί να παίρνει μόνο θετικές τιμές. όπου
όπου  . Παρατηρούμε επίσης ότι
. Παρατηρούμε επίσης ότι  . Από την ανισότητα AM-GM έχουμε
. Από την ανισότητα AM-GM έχουμε 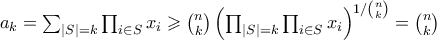 . Από εδώ πιστεύω είναι γνωστό πως συνεχίζουμε.
. Από εδώ πιστεύω είναι γνωστό πως συνεχίζουμε.
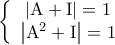
 που απορρίπτεται
που απορρίπτεται

 και
και 
 .
. .
. για κάποια
για κάποια 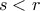 και άρα
και άρα  .
. είναι συνεχώς παραγωγίσιμη. Θα βάλω και εγώ αργότερα μια διαφορετική λύση (ελπίζω σωστή) που ούτε αυτή χρησιμοποιεί την συνθήκη.
είναι συνεχώς παραγωγίσιμη. Θα βάλω και εγώ αργότερα μια διαφορετική λύση (ελπίζω σωστή) που ούτε αυτή χρησιμοποιεί την συνθήκη.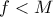 είναι φραγμένη τότε το ολοκλήρωμα είναι μεγαλύτερο από
είναι φραγμένη τότε το ολοκλήρωμα είναι μεγαλύτερο από 


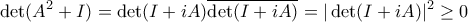 κ.τ.λ.,
κ.τ.λ., και
και  , όποτε
, όποτε 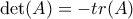 .
. , κ.τ.λ.
, κ.τ.λ. είναι μηδενικός τότε τελειώσαμε.
είναι μηδενικός τότε τελειώσαμε. .
. .
.

 .
. , και
, και  , οπότε
, οπότε 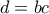 .
. και
και  ή
ή  και
και  .
. είναι
είναι  ή
ή  και για το
και για το 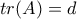 είναι
είναι  ή
ή