Χωρίς τριγωνομετρία

Ιστοσελίδα · #1

: shape.png (6.4 KiB) Προβλήθηκε 1161 φορές

Το

είναι τετράγωνο, του οποίου ζητείται η πλευρά

.

Στο παρελθόν έχουμε δει παρεμφερείς ασκήσεις στο . Δεκτές όλες οι λύσεις, αλλά η πρόκληση είναι να λυθεί χωρίς τριγωνομετρία.

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ · #2

Μιχάλης Νάννος έγραψε: ↑
Πέμ Ιούλ 18, 2019 11:12 am
shape.pngΤο είναι τετράγωνο, του οποίου ζητείται η πλευρά .

Στο παρελθόν έχουμε δει παρεμφερείς ασκήσεις στο . Δεκτές όλες οι λύσεις, αλλά η πρόκληση είναι να λυθεί χωρίς τριγωνομετρία.

Καλημέρα!

Έστω L,N

οι ορθές προβολές του

πάνω στις

αντίστοιχα.
Θέτω AL=x

και

Με πυθαγόρειο στα ALE,LED

: $\left\{\begin{matrix} &x^2=1-y^2 & \\ & y^2=7-(a-x)^2 \,\,(1)& \end{matrix}\right.\overset{(1)}{\Rightarrow }x^2=1-\left ( 7-(a-x)^2 \right )\Leftrightarrow x=\dfrac{a^2-6}{2a}$

Με πυθαγόρειο στο NEB

: $x^2=9-(a-y)^2\overset{y^2=1-x^2}{\Leftrightarrow} y=\dfrac{a^2-8}{2a}$

Έτσι έχουμε $x^2+y^2=1\Leftrightarrow \dfrac{a^4-12a^2+36+a^4-16a^2+64}{4a^2}=1\Leftrightarrow a^4-16a^2+50=0$
Λύνοντας την εξίσωση κρατάμε την λύση $a=\sqrt{8+\sqrt{14}}$

: 91.PNG (15.48 KiB) Προβλήθηκε 1132 φορές

Ιστοσελίδα · #3

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ έγραψε: ↑
Πέμ Ιούλ 18, 2019 12:22 pm

Μιχάλης Νάννος έγραψε: ↑
Πέμ Ιούλ 18, 2019 11:12 am
shape.pngΤο είναι τετράγωνο, του οποίου ζητείται η πλευρά .

Στο παρελθόν έχουμε δει παρεμφερείς ασκήσεις στο . Δεκτές όλες οι λύσεις, αλλά η πρόκληση είναι να λυθεί χωρίς τριγωνομετρία.

Καλημέρα!

Έστω οι ορθές προβολές του πάνω στις αντίστοιχα.
Θέτω και
Με πυθαγόρειο στα : $\left\{\begin{matrix} &x^2=1-y^2 & \\ & y^2=7-(a-x)^2 \,\,(1)& \end{matrix}\right.\overset{(1)}{\Rightarrow }x^2=1-\left ( 7-(a-x)^2 \right )\Leftrightarrow x=\dfrac{a^2-6}{2a}$

Με πυθαγόρειο στο : $x^2=9-(a-y)^2\overset{y^2=1-x^2}{\Leftrightarrow} y=\dfrac{a^2-8}{2a}$

Έτσι έχουμε $x^2+y^2=1\Leftrightarrow \dfrac{a^4-12a^2+36+a^4-16a^2+64}{4a^2}=1\Leftrightarrow a^4-16a^2+50=0$
Λύνοντας την εξίσωση κρατάμε την λύση $a=\sqrt{8+\sqrt{14}}$

91.PNG

Ολόσωστος, ταχύτατος και εντός πρόκλησης!

Μιχάλης Τσουρακάκης · #4

Μιχάλης Νάννος έγραψε: ↑
Πέμ Ιούλ 18, 2019 11:12 am
shape.pngΤο είναι τετράγωνο, του οποίου ζητείται η πλευρά .

Στο παρελθόν έχουμε δει παρεμφερείς ασκήσεις στο . Δεκτές όλες οι λύσεις, αλλά η πρόκληση είναι να λυθεί χωρίς τριγωνομετρία.

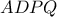$\displaystyle ADPQ$ είναι το συμμετρικό του $\displaystyle ABCD$ ως προς την $\displaystyle AD$

Με θ.διαμέσου στο $\displaystyle \vartriangle QEB \Rightarrow Q{E^2} + 7 = 2{a^2} \Rightarrow Q{E^2} + E{D^2} = Q{D^2} \Rightarrow \angle QED = {90^0}$

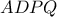Έτσι,ο περίκυκλος του $\displaystyle ADPQ$ περνά από το $\displaystyle E$ και $\displaystyle \angle QEA = {45^0} \Rightarrow \angle AED = {135^0}$

Εύκολα τώρα με ν.συνημιτόνου στο $\displaystyle \vartriangle AED$ παίρνουμε $\displaystyle \boxed{a = \sqrt {8 + \sqrt {14} } }$

: χωρίς τριγωνομετρία.png (12.52 KiB) Προβλήθηκε 1004 φορές

Altrian · #5

Στρέφουμε το $\bigtriangleup AED$ κατά

μοίρες γύρω από το

και παίρνουμε το $\bigtriangleup AFB$ .

$FB^{2}+FE^{2}=BE^{2}\Rightarrow \angle BFE=90.$ , Αλλά εκ κατασκευής BF,ED

κάθετες, άρα F,E,D

συνευθειακά.

$BD^{2}=BF^{2}+FD^{2}=7+7+2+2\sqrt{14}=2(8+\sqrt{14})\Rightarrow a=\sqrt{8+\sqrt{14}}$

Σταμ. Γλάρος · #6

Μιχάλης Νάννος έγραψε: ↑
Πέμ Ιούλ 18, 2019 11:12 am
shape.pngΤο είναι τετράγωνο, του οποίου ζητείται η πλευρά .

Στο παρελθόν έχουμε δει παρεμφερείς ασκήσεις στο . Δεκτές όλες οι λύσεις, αλλά η πρόκληση είναι να λυθεί χωρίς τριγωνομετρία.

Καλησπέρα. Μια προσπάθεια με Αναλυτική Γεωμετρία... Εκτός Φακέλου;

: Χωρίς τριγωνομετρία.png (60.39 KiB) Προβλήθηκε 866 φορές

Οι τρεις κύκλοι του σχήματος έχουν τις παρακάτω εξισώσεις :
(C_1): x^2 +y^2 =9

Λύνοντας το σύστημα των παραπάνω εξισώσεων βρίσκουμε τις συντεταγμένες
του σημείου τομής των τριών κύκλων.
Είναι: $E\left ( \dfrac{a^2-6}{2a},\dfrac{a^2+8}{2a} \right )$ .
Αντικαθιστώντας τις παραπάνω συντεταγμένες στην εξίσωση του κύκλου C_1

προκύπτει η εξίσωση : a^4 -16a^2 +50 = 0

.
Έχουμε δύο θετικές λύσεις :
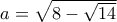Η $a= \sqrt{8-\sqrt{14}}$ απορρίπτεται , επειδή είναι μικρότερη από 3. (Βλ. σχήμα)
Άρα δεκτή είναι η $a= \sqrt{8+\sqrt{14}}$ .
Φιλικά
Σταμ. Γλάρος

#7

Μιχάλης Νάννος έγραψε: ↑
Πέμ Ιούλ 18, 2019 11:12 am
Το είναι τετράγωνο, του οποίου ζητείται η πλευρά .

Στο παρελθόν έχουμε δει παρεμφερείς ασκήσεις στο . Δεκτές όλες οι λύσεις, αλλά η πρόκληση είναι να λυθεί χωρίς τριγωνομετρία.

Μιχάλη καλησπέρα...

Στις ανωτέρω λύσεις ασφαλώς εννοείται ότι το σημείο $\displaystyle{E}$ είναι εντός του τετραγώνου για το λόγο αυτό απορρίφθηκε η δεύτερη λύση
που είναι:
$\displaystyle{a=\sqrt{8-\sqrt{14}} \ \ (1)}$

Αν όμως θεωρήσουμε ότι κι αυτή ικανοποιεί για τα τρίγωνα $\displaystyle{(ABE), (BED), (AED)}$ την τριγωνική ανισότητα, τότε θα μπορούσαμε
να τη δεχτούμε.

Τότε όμως το σημείο $\displaystyle{E}$ βρίσκεται εκτός του τριγώνου, όπως φαίνεται στο ακόλουθο σχήμα:

: Χωρίς τριγωνομετρία 1 (τετράγωνο).png (13.67 KiB) Προβλήθηκε 761 φορές

Το σχήμα κατασκευάστηκε με τα δεδομένα αυτά όπως και στην περίπτωση της πρώτης ρίζας.

Κώστας Δόρτσιος

Σημείωση:
Την ιδέα αυτή μου τη μετέφερε απόψε ο συνάδελφος Δημήτρης Ποτίκας σε μια κουβέντα μας. Πολλές φορές
κουβεντιάζω μαζί του θέματα γεωμετρίας με αρκετό ενδιάφέρον.

Χωρίς τριγωνομετρία

Χωρίς τριγωνομετρία

Re: Χωρίς τριγωνομετρία

Re: Χωρίς τριγωνομετρία

Re: Χωρίς τριγωνομετρία

Re: Χωρίς τριγωνομετρία

Re: Χωρίς τριγωνομετρία

Re: Χωρίς τριγωνομετρία

Μέλη σε σύνδεση