 η διαγώνιος
η διαγώνιος  είναι διάμετρος του περίκυκλου ενώ η
είναι διάμετρος του περίκυκλου ενώ η  διχοτόμος της
διχοτόμος της  .
. Οι
 τέμνονται στο
τέμνονται στο  . Αν είναι
. Αν είναι  και
και  τότε
τότε Να υπολογιστεί το εμβαδόν του περίκυκλου αυτού. Ευχαριστώ , Γιώργος.
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 η διαγώνιος
η διαγώνιος  είναι διάμετρος του περίκυκλου ενώ η
είναι διάμετρος του περίκυκλου ενώ η  διχοτόμος της
διχοτόμος της  .
.  τέμνονται στο
τέμνονται στο  . Αν είναι
. Αν είναι  και
και  τότε
τότε Καλημέρα Γιώργο!Γιώργος Μήτσιος έγραψε: ↑Κυρ Σεπ 22, 2019 2:03 amΚαλημέρα σε όλους.Τις ευχές μου στον συντονιστή του φακέλου , Στάθη Κούτρα για ΧΡΟΝΙΑ ΠΟΛΛΑ με ΥΓΕΙΑ!
Εμβαδόν περίκυκλου.PNG
Στο εγγεγραμμένο τετράπλευροη διαγώνιος
είναι διάμετρος του περίκυκλου ενώ η
διχοτόμος της
.
Οιτέμνονται στο
. Αν είναι
και
τότε
Να υπολογιστεί το εμβαδόν του περίκυκλου αυτού. Ευχαριστώ , Γιώργος.

 .
.  :
: 
 .
.  και έτσι η προηγούμενη δίδει :
και έτσι η προηγούμενη δίδει :  , ενώ η
, ενώ η  ,
, 

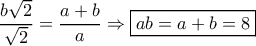


 Αν
Αν  είναι η ακτίνα του κύκλου. τότε
είναι η ακτίνα του κύκλου. τότε  και
και 


 Με νόμο συνημιτόνων στα τρίγωνα
Με νόμο συνημιτόνων στα τρίγωνα  έχω:
έχω:

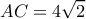 και
και  οπότε
οπότε 

 στο
στο 
 και το ζητούμενο εμβαδόν είναι
και το ζητούμενο εμβαδόν είναι 


 .
.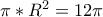
 .
. .
.  και
και  . Φιλικά , Γιώργος.
. Φιλικά , Γιώργος.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες