Διαιρέτης αθροίσματος

#1

Να αποδειχθεί ότι ο αριθμός 1000(1000+1)(1000^2+1)

διαιρεί το άθροισμα

$1000^1+1000^2+1000^3+...+1000^{1000}$

(Κατάλληλη για μαθητές Γυμνασίου).

Ορέστης Λιγνός · #2

Καλησπέρα κ. Μιχάλη!

Όμορφη άσκηση!

Έστω $x \in \mathbb{N^*}$ .

Έχω, $x^{1000}-1=(x^4)^{250}-1= (x^4-1)( \ldots)$ , άρα $x^4-1 \mid x^{1000}-1$ , οπότε $(x-1)(x+1)(x^2+1) \mid (x-1)(x^{999}+ \ldots +x+1)$ , άρα $(x+1)(x^2+1) \mid x^{999}+ \ldots +x+1$ .

Πολλαπλασιάζω τώρα και τα δύο μέλη της παραπάνω διαιρετότητας με

, και προκύπτει $x(x+1)(x^2+1) \mid x^{1000}+x^{999}+ \ldots +x$ .

Τέλος, θέτω x=1000

και παίρνω την προς απόδειξη!

#3

Mihalis_Lambrou έγραψε: ↑
Παρ Οκτ 25, 2019 11:01 am
Να αποδειχθεί ότι ο αριθμός διαιρεί το άθροισμα

$1000^1+1000^2+1000^3+...+1000^{1000}$

Ορέστη, Καλησπέρα.

Ωραιότατα.

Ας την δούμε και αλλιώς: Είναι x(x+1)(x^2+1)=x+x^2+x^3+x^4

. Χωρίζουμε το δοθέν άθροισμα σε

τετράδες και από κάθε μία βγάζουμε κοινό παράγοντα:

$\displaystyle{ (x+x^2+x^3+x^4) + x^4(x+x^2+x^3+x^4)+ x^8(x+x^2+x^3+x^4)+...+ x^{96}(x+x^2+x^3+x^4)}$

Βλέπουμε τώρα ότι το

είναι εκ νέου κοινός παράγοντας, από όπου το ζητούμενο (για x=1000

).

#4

Οι

είναι όλοι πρώτοι μεταξύ τους για

άρτιο. (Π.χ. επειδή n^2 + 1 - (n-1)(n+1) = 2

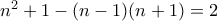, τότε ο μέγιστος κοινός διαιρέτηες των n+1,n^2+1

είναι ίσος με 1 ή 2. Για

άρτιο όμως δεν μπορεί να είναι ίσος με

.)

Τώρα παρατηρούμε ότι

$n + n^2 + \cdots + n^{1000} \equiv 0 \bmod n$
$n + n^2 + \cdots + n^{1000} \equiv -1 + 1 -1 + 1 + \cdots -1 + 1 \equiv 0 \bmod (n+1)$
και
$n + n^2 + \cdots + n^{1000} \equiv (n -1 - n + 1) + \cdots (n -1 - n + 1) \equiv 0 \bmod (n^2+1)$

Άρα κάθε ένας εκ των n,n+1,n^2+1

και άρα και το γινόμενό τους διαιρούν τον $n + n^2 + \cdots + n^{1000}$ για οποιοδήποτε άρτιο

.

Διαιρέτης αθροίσματος

Διαιρέτης αθροίσματος

Re: Διαιρέτης αθροίσματος

Re: Διαιρέτης αθροίσματος

Re: Διαιρέτης αθροίσματος

Μέλη σε σύνδεση