 , με
, με  , έχουμε "εγγράψει" τον ρόμβο
, έχουμε "εγγράψει" τον ρόμβο  .
.α) Δείξτε ότι ο ρόμβος καταλαμβάνει λιγότερη από το μισή επιφάνεια του τριγώνου.
β) Αν :
 , βρείτε το λόγο των πλευρών :
, βρείτε το λόγο των πλευρών : 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , με
, με  , έχουμε "εγγράψει" τον ρόμβο
, έχουμε "εγγράψει" τον ρόμβο  .
. , βρείτε το λόγο των πλευρών :
, βρείτε το λόγο των πλευρών : 
Αν
 τότε
τότε  και από την ομοιότητα των πράσινων τριγώνων με το μεγάλο έχουμε
και από την ομοιότητα των πράσινων τριγώνων με το μεγάλο έχουμε  . Ειδικά
. Ειδικά 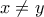 . Επίσης
. Επίσης 
 , από όπου το ζητούμενο.
, από όπου το ζητούμενο.  τότε
τότε  . Μαζί με την
. Μαζί με την  βρίσκουμε τα
βρίσκουμε τα  (άμεσο) και άρα το
(άμεσο) και άρα το  . Εδώ βγαίνει
. Εδώ βγαίνει  , και λοιπά.
, και λοιπά. , που είναι
, που είναι  όπως εννοεί ο Μιχάλης
όπως εννοεί ο Μιχάλης .
. του τριγώνου
του τριγώνου , ποια είναι η μέγιστη τιμή της διαφοράς ;
, ποια είναι η μέγιστη τιμή της διαφοράς ;Οπως έγραψε και ο κ. Λάμπρου (χρόνια πολλά με την ευκαιρία) έχουμε:KARKAR έγραψε: ↑Τετ Νοέμ 06, 2019 11:43 amΜικροδιαφορά επέκταση.pngΓια την απάντηση στα αρχικά ερωτήματα αρκεί ο λόγος, που είναι
όπως εννοεί ο Μιχάλης
με την έκφραση "και λοιπά" . Αν όμως θέλουμε να βρούμε έναν τύπο για την διαφορά αυτή ,
( το κόκκινο εξόγκωμα του Antrian ) , θα χρειασθούμε και την πλευρά.
Θέτω λοιπόν ένα πρόσθετο ερώτημα : Αν ο ρόμβος έχει εμβαδόν τοτου τριγώνου
και είναι γνωστή η μικρότερη πλευρά, ποια είναι η μέγιστη τιμή της διαφοράς ;
 .
. 
 .
. είναι διχοτόμος της
είναι διχοτόμος της  έχουμε ότι:
έχουμε ότι: 
 μεγιστοποιείται όταν
μεγιστοποιείται όταν 
 αυτού δηλ.
αυτού δηλ. 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες