 για
για ![x \in (0,1] x \in (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5f3bd0dafa13199e5ec59664dccbce7e.png) αν
αν 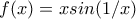
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

Τόλη η ερώτηση είναι λίγο παραπλανητική.Tolaso J Kos έγραψε: ↑Τετ Ιαν 08, 2020 10:01 pm
Σίγουρα υπολογίζεται το ολοκλήρωμα που προκύπτει στοιχειωδώς ;
Καλημέρα από τα Γρεβενά...
![\displaystyle{S_{OA}=\int_{0.01}^{1}ds=\int_{0.01}^{1}\sqrt{1+[f'(x)]^2]}dx \ \ (1) } \displaystyle{S_{OA}=\int_{0.01}^{1}ds=\int_{0.01}^{1}\sqrt{1+[f'(x)]^2]}dx \ \ (1) }](/forum/ext/geomar/texintegr/latexrender/pictures/a4ea8b4f079a15e009627622f95496a3.png)


![\displaystyle{I=[0.01, 1]} \displaystyle{I=[0.01, 1]}](/forum/ext/geomar/texintegr/latexrender/pictures/9d6c44cee0ed33eedd32187857672577.png)
Αν και ο Σταύρος έδωσε τον τόνο ότι κάτι άλλο να περιμένεις, φαίνεται ότι δεν έγινε κατανοητός.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Ιαν 08, 2020 10:55 pmΤόλη η ερώτηση είναι λίγο παραπλανητική.
Λέει να βρεθεί.Οχι να υπολογιστεί.
Αρα .......
 όπου
όπου  έχει μήκος μικρότερο ή ίσο της δοθείσας. Χρησιμοποίησε τώρα το γεγονός ότι η σειρά
έχει μήκος μικρότερο ή ίσο της δοθείσας. Χρησιμοποίησε τώρα το γεγονός ότι η σειρά  , αποκλίνει.
, αποκλίνει.Μιχάλη έχεις δίκιο!Mihalis_Lambrou έγραψε: ↑Πέμ Ιαν 09, 2020 9:01 amΑν και ο Σταύρος έδωσε τον τόνο ότι κάτι άλλο να περιμένεις, φαίνεται ότι δεν έγινε κατανοητός.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Ιαν 08, 2020 10:55 pmΤόλη η ερώτηση είναι λίγο παραπλανητική.
Λέει να βρεθεί.Οχι να υπολογιστεί.
Αρα .......
Επανέρχομαι λοιπόν.
Η παραπάνω συνάρτηση είναι το στάνταρ παράδειγμα καμπύλης που έχει άπειρο μήκος.
...........................................................................................................
 έως και την τιμή
έως και την τιμή  με αποτέλεσμα να προκύψει:
με αποτέλεσμα να προκύψει: 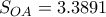 με προσέγγιση τέσσερα δεκαδικά ψηφία.
με προσέγγιση τέσσερα δεκαδικά ψηφία. όπου προέκυψαν σαφώς μεγαλύτερες τιμές του μήκους
όπου προέκυψαν σαφώς μεγαλύτερες τιμές του μήκους  , για παράδειγμα,
, για παράδειγμα,
 μέχρι και το
μέχρι και το  το μήκος της καμπύλης αυτής να είναι άπειρο!
το μήκος της καμπύλης αυτής να είναι άπειρο! χρόνια πριν, όταν τα λογισμικά ήταν καινούργια και είχε γίνει της μόδας η συζήτηση για αξιοποίησή τους στη έρευνα και στην διαδασκαλία μας, είχε οργανώσει το Βαρβάκειο μία σχετική ημερίδα. Ο εγκέφαλος από πίσω ήταν το μέλος μας, ο Ζήνων Λυγάτσικας (απολαύστε το site του εδώ).
χρόνια πριν, όταν τα λογισμικά ήταν καινούργια και είχε γίνει της μόδας η συζήτηση για αξιοποίησή τους στη έρευνα και στην διαδασκαλία μας, είχε οργανώσει το Βαρβάκειο μία σχετική ημερίδα. Ο εγκέφαλος από πίσω ήταν το μέλος μας, ο Ζήνων Λυγάτσικας (απολαύστε το site του εδώ).  έως το
έως το  συμπεριφέρεται ως (σταθερά επί)
συμπεριφέρεται ως (σταθερά επί)  . Οπότε η απόκλιση είναι αργή. Για παράδειγμα το
. Οπότε η απόκλιση είναι αργή. Για παράδειγμα το  έχει λογάριθμο
έχει λογάριθμο  . Αν το διπλασιάσουμε σε
. Αν το διπλασιάσουμε σε  , ο λογάριθμος γίνεται
, ο λογάριθμος γίνεται  , δηλαδή μία αύξηση ούτε
, δηλαδή μία αύξηση ούτε  .
.Ας δούμε ένα παράδειγμα όπου το λογισμικό μας τα θαλασσώνει.Mihalis_Lambrou έγραψε: ↑Πέμ Ιαν 09, 2020 10:48 pmΣυγκεκριμένα, είχα βρει μερικά ωραιότατα παραδείγματα όπου είτε το λογισμικό τα θαλασσώνει, είτε λέει μεν την σωστή απάντηση αλλά εμείς δεν την αποκωδικοποιούμε σωστά.
 δεκαδικών ψηφίων. Για παράδειγμα, αντί για
δεκαδικών ψηφίων. Για παράδειγμα, αντί για  το λογισμικό μας γράφει
το λογισμικό μας γράφει  .
. και για
και για  είναι
είναι  .
.  για κάθε
για κάθε  .
. δεκαδικών ψηφίων. Τι θα βρείτε ως τιμές των, ας πούμε,
δεκαδικών ψηφίων. Τι θα βρείτε ως τιμές των, ας πούμε,  ; Πόσο καλές τιμές είναι αυτές;
; Πόσο καλές τιμές είναι αυτές;  χωριστά, στην περίπτωση που δουλεύετε με ή χωρίς λογισμικό.
χωριστά, στην περίπτωση που δουλεύετε με ή χωρίς λογισμικό.  δεκαδικά ψηφία, δεν αλλάζει την ουσία. Θα εμφανιστεί το ίδιο φαινόμενο
δεκαδικά ψηφία, δεν αλλάζει την ουσία. Θα εμφανιστεί το ίδιο φαινόμενο δεκαδικά).
δεκαδικά).Μιχάλη, με αφορμή τη σχέση των λογισμικών, που ακόμα στην χώρα μας, νομίζω ότι είναι "εκτός παιχνιδιού",Mihalis_Lambrou έγραψε: ↑Σάβ Ιαν 11, 2020 6:15 pmΑς δούμε ένα παράδειγμα όπου το λογισμικό μας τα θαλασσώνει.Mihalis_Lambrou έγραψε: ↑Πέμ Ιαν 09, 2020 10:48 pmΣυγκεκριμένα, είχα βρει μερικά ωραιότατα παραδείγματα όπου είτε το λογισμικό τα θαλασσώνει, είτε λέει μεν την σωστή απάντηση αλλά εμείς δεν την αποκωδικοποιούμε σωστά.

 με την εντολή να γραφεί σε δεκαδική μορφή με έξι δεκαδικά ψηφία.
με την εντολή να γραφεί σε δεκαδική μορφή με έξι δεκαδικά ψηφία.Θα συμφωνήσω.
Ακριβώς. Ας συμπληρώσω ότι αν κάνεις δεκαδική προσέγγιση, όσο καλή και αν είναι, στο συγκεκριμένο παράδειγμα η σταθερή ακολουθίαKDORTSI έγραψε: ↑Σάβ Ιαν 11, 2020 10:21 pm
Λογισμικό Maple
Εδώ τα πράγματα είναι διαφορετικά!
Στην πρώτη γραμμή έχει εισαχθεί ο αριθμόςμε την εντολή να γραφεί σε δεκαδική μορφή με έξι δεκαδικά ψηφία.
Το αποτέλεσμα που προέκυψε δόθηκε για υπολογισμό του δεύτερου όρου κλπ. Το αποτέλεσμα είναι εντελώς διαφορετικό και όχι αυτό
που θα ανέμενε κανείς!
 φέρεται να αποκλίνει στο πλην άπειρο. Χάος, δηλαδή.
φέρεται να αποκλίνει στο πλην άπειρο. Χάος, δηλαδή.Νίκο, κάποια πρόοδος εδώ;Mihalis_Lambrou έγραψε: ↑Πέμ Ιαν 09, 2020 9:01 amΔίνω υπόδειξη μόνο για να μας γράψει ο θεματοθέτης Nikos127 λύση, αν και μάλλον ματαιοπονώ γιατί σε άλλες περιπτώσεις (βλέπε εδώ) μας αγνόησε: Ρωτάει δηλαδή την λύση άσκησης που συνάντησε σε μαθήματα που παρακολουθεί αλλά που δεν κατάφερε να λύσει (μέχρι εδώ όλα καλά) αλλά μετά ... εξαφανίζεται.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες