 με
με 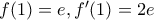
και
 , για κάθε
, για κάθε 
Αν για κάθε
 ισχύει
ισχύει 
i) Να δείξετε ότι η
 είναι κυρτή.
είναι κυρτή.ii) Να δείξετε ότι
 για κάθε
για κάθε 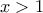 .
.iii) Να βρείτε το σύνολο τιμών της
 .
.iv) Να λύσετε στο διάστημα
 την εξίσωση
την εξίσωση 
Συντονιστής: Μπάμπης Στεργίου
 με
με 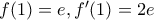
 , για κάθε
, για κάθε 
 ισχύει
ισχύει 
 είναι κυρτή.
είναι κυρτή. για κάθε
για κάθε 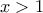 .
. .
. την εξίσωση
την εξίσωση 
...λίγο πρινΛάμπρος Κατσάπας έγραψε: ↑Παρ Μαρ 20, 2020 11:16 pmΈστω η δύο φορές παραγωγίσιμη συνάρτησημε
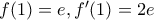
και, για κάθε
Αν για κάθεισχύει
i) Να δείξετε ότι ηείναι κυρτή.
ii) Να δείξετε ότιγια κάθε
.
iii) Να βρείτε το σύνολο τιμών της.
iv) Να λύσετε στο διάστηματην εξίσωση

 και επειδή
και επειδή  , συνεχής έχει σταθερό πρόσημο ,
, συνεχής έχει σταθερό πρόσημο ,  άρα
άρα  ισχύει
ισχύει  άρα
άρα  είναι κυρτή.
είναι κυρτή. γι αυτό θεωρούμε
γι αυτό θεωρούμε  με
με  και
και  και
και  και
και  που από δεδομένα
που από δεδομένα  επομένως η
επομένως η  γνήσια αύξουσα στο
γνήσια αύξουσα στο  άρα
άρα  που σημαίνει
που σημαίνει  γνήσια αύξουσα στο
γνήσια αύξουσα στο 
 που είναι αυτό που θέλαμε.
που είναι αυτό που θέλαμε. επειδή
επειδή  το
το  και από
και από  έχουμε ότι
έχουμε ότι  άρα η
άρα η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  έτσι
έτσι 
 και επειδή
και επειδή  από (ιιι) και
από (ιιι) και  η ισότητα ισχύει όταν
η ισότητα ισχύει όταν 
 που επαληθεύεται όταν
που επαληθεύεται όταν  , έτσι μοναδική λύση της εξίσωσης είναι το
, έτσι μοναδική λύση της εξίσωσης είναι το  .
. , για κάθε
, για κάθε  δεν χρειάζεται στις υποθέσεις.
δεν χρειάζεται στις υποθέσεις. με
με  τότε η σχέση δίνει
τότε η σχέση δίνει  ΑΤΟΠΟ.
ΑΤΟΠΟ. η
η  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα. θα είναι
θα είναι  οπότε η
οπότε η  γνησίως αύξουσα.
γνησίως αύξουσα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες