 Για το δευτεροβάθμιο τριώνυμο
Για το δευτεροβάθμιο τριώνυμο  , ισχύει :
, ισχύει :  , για κάθε
, για κάθε  .
.α) Υπολογίστε το

β) Υπολογίστε το

γ) Υπολογίστε τον θετικό
 , για τον οποίο :
, για τον οποίο : 
δ) Πόσες λύσεις έχει η εξίσωση :
 , για τις διάφορες τιμές του πραγματικού
, για τις διάφορες τιμές του πραγματικού  ;
;Συντονιστής: exdx
 Για το δευτεροβάθμιο τριώνυμο
Για το δευτεροβάθμιο τριώνυμο  , ισχύει :
, ισχύει :  , για κάθε
, για κάθε  .
.

 , για τον οποίο :
, για τον οποίο : 
 , για τις διάφορες τιμές του πραγματικού
, για τις διάφορες τιμές του πραγματικού  ;
;Δεν χρειάζεται να ξέρουμε ότι η
 είναι δευτεροβάθμιο τριώνυμο. Στην δοσμένη σχέση θέτω όπου
είναι δευτεροβάθμιο τριώνυμο. Στην δοσμένη σχέση θέτω όπου  το
το  και προκύπτει
και προκύπτει 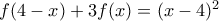 ,
, , που δίνει
, που δίνει  .
. ,
, ,
, , προκύπτει
, προκύπτει  , οπότε
, οπότε 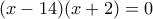 , συνεπώς
, συνεπώς  , αφού
, αφού  .
.  γράφεται
γράφεται  . Η Διακρίνουσα
. Η Διακρίνουσα  .
. 2 λύσεις, αν
2 λύσεις, αν  , δηλαδή
, δηλαδή  ,
, 1 λύση, αν
1 λύση, αν  , δηλαδή
, δηλαδή 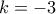 ,
, καμία λύση, αν
καμία λύση, αν  , δηλαδή
, δηλαδή  .
.Σωστά. Για χάρη των μαθητών ας δούμε τι θα συναντούσε κάποιος λύτης που πήγαινε με τριώνυμο,Ορέστης Λιγνός έγραψε: ↑Κυρ Μαρ 29, 2020 1:40 pmΔεν χρειάζεται να ξέρουμε ότι ηείναι δευτεροβάθμιο τριώνυμο.
 .
. . Συγκρίνοντας (*) συντελεστή του
. Συγκρίνοντας (*) συντελεστή του  έχουμε
έχουμε  , από όπου το
, από όπου το  . Από τον συντελεστή του
. Από τον συντελεστή του  βγαίνει εύκολα το
βγαίνει εύκολα το  και από τον σταθερό όρο βγαίνει τώρα το
και από τον σταθερό όρο βγαίνει τώρα το  . Και λοιπά.
. Και λοιπά. για κάθε
για κάθε  πραγματικό, δείξτε ότι
πραγματικό, δείξτε ότι 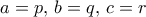 .
. Έστω το πολυώνυμο
 . Από την συνθήκη είναι
. Από την συνθήκη είναι  , και είναι
, και είναι 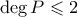 , άρα πρέπει
, άρα πρέπει  , δηλαδή
, δηλαδή  .
.Ορέστη, εδώ έχουμε ένα λεπτό σημείο: Για να μιλήσουμε για βαθμό πολυωνύμου (ακριβέστερα, πολυωνυμική συνάρτηση) προϋποθέτει ότι έχουμε αποδείξει ότι η παράσταση είναι μοναδική.Ορέστης Λιγνός έγραψε: ↑Κυρ Μαρ 29, 2020 2:48 pmΈστω το πολυώνυμο. Από την συνθήκη είναι
, και είναι
, άρα πρέπει
, δηλαδή
.
 (δηλαδή
(δηλαδή  ) έχουμε ότι τα τριώνυμα
) έχουμε ότι τα τριώνυμα  και
και  είναι ίσα!
είναι ίσα! 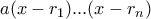 όπου
όπου  οι ρίζες. Για παράδειγμα στο
οι ρίζες. Για παράδειγμα στο  το
το  έχει τέσσερις(!) ρίζες,
έχει τέσσερις(!) ρίζες,  και δύο γραφές
και δύο γραφές  .
.Νομίζω ότι κάτι αλλο θες να γράψεις Μιχάλη,Mihalis_Lambrou έγραψε: ↑Κυρ Μαρ 29, 2020 3:24 pmΑυτό στους πραγματικούς ή μιγαδικούς αριθμούς είναι σωστό, αλλά πρέπει να αποδειχθεί. Δεν ισχύει το ίδιο όταν το σύνολα αναφοράς είναι άλλοι αριθμοί. Μιλώντας εκτός ύλης, αν δουλεύαμε στο(δηλαδή
) έχουμε ότι τα τριώνυμα
και
είναι ίσα!
 και
και  στο
στο  είναι ίσα σαν συναρτήσεις.
είναι ίσα σαν συναρτήσεις.
Σταύρο, λέω ακριβώς αυτό που λες και εσύ.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Μαρ 29, 2020 4:31 pm
Νομίζω ότι κάτι αλλο θες να γράψεις Μιχάλη,
προφανώς γνωρίζεις τα παρακάτω.
Τακαι
στο
είναι ίσα σαν συναρτήσεις.
Σαν πολυώνυμα δεν είναι ίσα.
Ειναι άλλο πολυώνυμο και άλλο πολυωνιμική συνάρτηση.
Στα
οι έννοιες ταυτίζονται.
Γράφω την απόδειξη που ζήταγα.Mihalis_Lambrou έγραψε: ↑Κυρ Μαρ 29, 2020 3:24 pmΓια να μιλήσουμε για βαθμό πολυωνύμου (ακριβέστερα, πολυωνυμική συνάρτηση) προϋποθέτει ότι έχουμε αποδείξει ότι η παράσταση είναι μοναδική.
 για κάθε
για κάθε  πραγματικό. Τότε για
πραγματικό. Τότε για  παίρνομε
παίρνομε  , οπότε
, οπότε  . Διαιρώντας με
. Διαιρώντας με  έπεται
έπεται  για κάθε
για κάθε  .
.  , οπότε
, οπότε  , και από εκεί εύκολα
, και από εκεί εύκολα  . Αν δεν ξέρουμε από όρια, τότε για
. Αν δεν ξέρουμε από όρια, τότε για  παίρνουμε
παίρνουμε 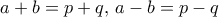 , αντίστοιχα. Με πρόσθεση κατά μέλη έπεται
, αντίστοιχα. Με πρόσθεση κατά μέλη έπεται  , και άρα
, και άρα  .
.

 στο
στο 

 στο
στο 
 με
με 
Σωστά. Ας το δούμε με τον περιορισμόΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Μαρ 29, 2020 6:59 pmΑπό ότι βλέπω μπορεί με στοιχειώδη μέσα (ύλη Α Λυκείου)
να αποδειχθεί το εξής:
Αν
και
πραγματικοί ώστε
Για κάθεστο
είναι
τότε
Σημείωση .Το για κάθεστο
μπορεί να αντικατασταθεί με το
για κάθεμε

 που γράφεις. Βλέπω διάφορες λύσεις αλλά για την ώρα
που γράφεις. Βλέπω διάφορες λύσεις αλλά για την ώρα  έχουμε
έχουμε 

 τότε
τότε  και από το προηγούμενο είναι
και από το προηγούμενο είναι  , όπως θέλαμε. Αλλιώς δεν μπορεί να είναι
, όπως θέλαμε. Αλλιώς δεν μπορεί να είναι  γιατί θέτοντας
γιατί θέτοντας  στην
στην 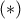 οποιονδήποτε θετικό αριθμό μικρότερο του
οποιονδήποτε θετικό αριθμό μικρότερο του  και του
και του  έπεται
έπεται  , άτοπο.
, άτοπο. , και λοιπά.
, και λοιπά.Ακριβώς τα ίδια είχα στο μυαλό μου με την εξης διαφορά.Mihalis_Lambrou έγραψε: ↑Κυρ Μαρ 29, 2020 7:31 pmΣωστά. Ας το δούμε με τον περιορισμόΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Μαρ 29, 2020 6:59 pmΑπό ότι βλέπω μπορεί με στοιχειώδη μέσα (ύλη Α Λυκείου)
να αποδειχθεί το εξής:
Αν
και
πραγματικοί ώστε
Για κάθεστο
είναι
τότε
Σημείωση .Το για κάθεστο
μπορεί να αντικατασταθεί με το
για κάθεμε

που γράφεις. Βλέπω διάφορες λύσεις αλλά για την ώρα
προτιμώ την εξής:
Για κάθε τέτοιοέχουμε
Αντότε
και από το προηγούμενο είναι
, όπως θέλαμε. Αλλιώς δεν μπορεί να είναι
γιατί θέτοντας
στην
οποιονδήποτε θετικό αριθμό μικρότερο του
και του
έπεται
, άτοπο.
Όμοια, και λοιπά.

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες