α) Βρείτε όλους τους πρώτους
 τέτοιους ώστε
τέτοιους ώστε  και οι αριθμοί
και οι αριθμοί  και
και  να είναι τέλεια τετράγωνα.
να είναι τέλεια τετράγωνα.β) Υπάρχουν πρώτοι
 τέτοιοι ώστε
τέτοιοι ώστε  και οι αριθμοί
και οι αριθμοί  και
και  να είναι τέλεια τετράγωνα;
να είναι τέλεια τετράγωνα;ΘΕΜΑ 2
Δίνεται το σύνολο
 .
.Να βρεθεί η μέγιστη τιμή του
 για την οποία υπάρχουν σύνολα
για την οποία υπάρχουν σύνολα  τέτοια ώστε
τέτοια ώστε  , και κανένα από αυτά δεν περιέχει την μέση τιμή δύο οποιονδήποτε στοιχείων του.
, και κανένα από αυτά δεν περιέχει την μέση τιμή δύο οποιονδήποτε στοιχείων του.Για την τιμή του
 που θα βρείτε, να προσδιορίσετε το πλήθος των συνόλων
που θα βρείτε, να προσδιορίσετε το πλήθος των συνόλων 
ΘΕΜΑ 3
Να βρείτε τη μέγιστη και την ελάχιστη τιμή της παράστασης

όταν τα
 και
και  διατρέχουν το σύνολο των θετικών πραγματικών αριθμών.
διατρέχουν το σύνολο των θετικών πραγματικών αριθμών.ΘΕΜΑ 4
Θεωρούμε τρίγωνο
 , το έγκεντρό του
, το έγκεντρό του  , το σημείο επαφής
, το σημείο επαφής  του εγγεγραμμένου κύκλου με την
του εγγεγραμμένου κύκλου με την  και τη διχοτόμο του
και τη διχοτόμο του 
Αν
 το μέσο του τόξου
το μέσο του τόξου  του περιγεγραμμένου κύκλου του, που περιέχει το
του περιγεγραμμένου κύκλου του, που περιέχει το  και
και  να αποδείξετε ότι η ευθεία
να αποδείξετε ότι η ευθεία  διέρχεται από το μέσο του τμήματος
διέρχεται από το μέσο του τμήματος 

 πρώτοι και
πρώτοι και  ταυτόχρονα τέλεια τετράγωνα τότε (τουλάχιστον) ένας εκ των
ταυτόχρονα τέλεια τετράγωνα τότε (τουλάχιστον) ένας εκ των  .
.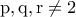 .Τότε
.Τότε  .Άρα για να είναι
.Άρα για να είναι 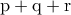 τέλειο τετράγωνο πρέπει
τέλειο τετράγωνο πρέπει  .Αν ήταν
.Αν ήταν 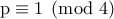 τότε πρέπει
τότε πρέπει  άρα έστω
άρα έστω  (ή το αντίστροφο,δεν έχει σημασία).Τότε όμως είναι
(ή το αντίστροφο,δεν έχει σημασία).Τότε όμως είναι  άτοπο αφού το
άτοπο αφού το 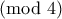 .Όμοια καταλήγουμε σε άτοπο όταν
.Όμοια καταλήγουμε σε άτοπο όταν 
 .Έστω
.Έστω  .Πρέπει
.Πρέπει  άρα
άρα  άρα
άρα  (αφού
(αφού  .Τότε όμως
.Τότε όμως  άτοπο αφού το
άτοπο αφού το  .
. (ή
(ή  ,δεν έχει σχέση) και έτσι
,δεν έχει σχέση) και έτσι  με
με  φυσικό.Επειδή το αριστερό μέλος είναι γινόμενο πρώτων έχουμε τις εξής περιπτώσεις:
φυσικό.Επειδή το αριστερό μέλος είναι γινόμενο πρώτων έχουμε τις εξής περιπτώσεις: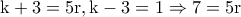 άτοπο.
άτοπο.
 άτοπο.
άτοπο. και οι αναδιατάξεις.
και οι αναδιατάξεις. (χρησιμοποιούμε τον ισχυρισμό και σχέσεις
(χρησιμοποιούμε τον ισχυρισμό και σχέσεις  οπότε με δοκιμές καταλήγουμε σε αυτή)
οπότε με δοκιμές καταλήγουμε σε αυτή) αλλά η λύση μου είναι μάλλον πολύπλοκη για "μικρούς". Θα περιμένω να δω κάτι άλλο πριν την αναρτήσω.
αλλά η λύση μου είναι μάλλον πολύπλοκη για "μικρούς". Θα περιμένω να δω κάτι άλλο πριν την αναρτήσω. ως άμεση εφαρμογή της ανισότητας Cauchy-Schwarz και πιάνεται όταν
ως άμεση εφαρμογή της ανισότητας Cauchy-Schwarz και πιάνεται όταν 
 με
με ![\displaystyle{t\in \left(0,\frac{1}{2}\right].} \displaystyle{t\in \left(0,\frac{1}{2}\right].}](/forum/ext/geomar/texintegr/latexrender/pictures/fede94bfc29c17b32396afeadbc3273c.png)
 .
.

 (1)
(1)


 βαθμού συν το ότι η εξίσωση που προκύπτει είναι συμμετρική τετάρτου βαθμού.
βαθμού συν το ότι η εξίσωση που προκύπτει είναι συμμετρική τετάρτου βαθμού. 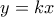 , και έστω ότι το δεδομένο κλασμα πάιρνει την τιμή
, και έστω ότι το δεδομένο κλασμα πάιρνει την τιμή  , τότε η εξίσωση
, τότε η εξίσωση 
 . Η εξίσωση αυτή γράφεται
. Η εξίσωση αυτή γράφεται 
 , διαιρούμε με
, διαιρούμε με  και έχουμε
και έχουμε
 , θέτουμε
, θέτουμε  και έχουμε
και έχουμε


 έχουμε τις επιπλέον συνθήκες οι ρίζες της παραπάνω εξίσωσης να είναι μεγαλύτερες ή ίσες του
έχουμε τις επιπλέον συνθήκες οι ρίζες της παραπάνω εξίσωσης να είναι μεγαλύτερες ή ίσες του  που μηδενίζει τον συντελεστή του δευτεροβάθμιου όρου ξεχωριστά. Οπότε πρέπει να εξετάσουμε και τις ανισότητες
που μηδενίζει τον συντελεστή του δευτεροβάθμιου όρου ξεχωριστά. Οπότε πρέπει να εξετάσουμε και τις ανισότητες
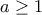 .
. .Η τετράδα
.Η τετράδα  είναι αρμονική άρα αρκεί
είναι αρμονική άρα αρκεί  .
.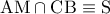 .Στο
.Στο 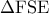 το
το  είναι ορθόκεντρο άρα
είναι ορθόκεντρο άρα  .Αρκεί λοιπόν να δείξω ότι
.Αρκεί λοιπόν να δείξω ότι  .Για να ισχύει αυτό αρκεί
.Για να ισχύει αυτό αρκεί 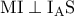 καθώς τότε το
καθώς τότε το  .
. .Είναι γνωστό ότι
.Είναι γνωστό ότι  .Είναι
.Είναι  άρα
άρα  .Έτσι αν
.Έτσι αν  η παράλληλη από το
η παράλληλη από το 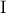 στην
στην  (στο σχήμα η πορτοκαλί διακεκομμένη) τότε σχηματίζεται η αρμονική δέσμη
(στο σχήμα η πορτοκαλί διακεκομμένη) τότε σχηματίζεται η αρμονική δέσμη 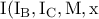 .Επίσης και η δέσμη
.Επίσης και η δέσμη  είναι αρμονική.Παρατηρούμε πως οι δύο αυτές δέσμες έχουν κάθετα τα τρία ζεύγη ομόλογων ακτίνων τους άρα και το τέταρτο,δηλαδή τις
είναι αρμονική.Παρατηρούμε πως οι δύο αυτές δέσμες έχουν κάθετα τα τρία ζεύγη ομόλογων ακτίνων τους άρα και το τέταρτο,δηλαδή τις  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε. , οπότε εύκολα προκύπτει ότι
, οπότε εύκολα προκύπτει ότι  .
.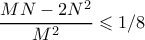
 , οπότε
, οπότε  .
. ύψος του
ύψος του  μέσο της
μέσο της  με διατέμνουσα την
με διατέμνουσα την 
 (1)
(1)


 και η (1) δίνει
και η (1) δίνει 

 του
του  ως προς το
ως προς το  πως
πως  και επομένως αρκεί
και επομένως αρκεί  .Είναι όμως στο σχήμα του Προδρόμου
.Είναι όμως στο σχήμα του Προδρόμου  από συμμετρική αντιστροφή που δίνει το ζητούμενο
από συμμετρική αντιστροφή που δίνει το ζητούμενο