 .
.Ανίσωση με λίγο απόλυτο
Συντονιστής: stranton
- Al.Koutsouridis
- Δημοσιεύσεις: 1798
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
- Al.Koutsouridis
- Δημοσιεύσεις: 1798
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13278
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ανίσωση με λίγο απόλυτο
Al.Koutsouridis έγραψε: ↑Δευ Μάιος 04, 2020 8:08 pmΩραία! Να δούμε όμως πως γίνονται και οι παραγοντοποιήσεις.




 Εύκολα με Horner αλλά είναι εκτός φακέλου.
Εύκολα με Horner αλλά είναι εκτός φακέλου.Αλλιώς με το ίδιο σκεπτικό όπως στην προηγούμενη:


Για το πρόσημο της πρώτης παράστασης, χωρίς παραγοντοποίηση είναι:

- Al.Koutsouridis
- Δημοσιεύσεις: 1798
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ανίσωση με λίγο απόλυτο
Άλλη μια λύση με τεχνικές που έχουμε δει πολλάκις στο 
παρατηρούμε ότι η ανίσωση γράφεται
 .
.


 .
.
Θέτουμε , τότε η ανίσωση γράφεται
, τότε η ανίσωση γράφεται
 και την οποία μελετάμε σαν δευτεροβάθμιο τριώνυμο. Οι ρίζες της εξίσωσης
και την οποία μελετάμε σαν δευτεροβάθμιο τριώνυμο. Οι ρίζες της εξίσωσης  είναι
είναι
 και
και  . Έτσι η ανίσωση παίρνει την μορφή
. Έτσι η ανίσωση παίρνει την μορφή
 .
.
Στην τελαυταία, παραγοντοποιημένη πλέον, ανίσωση μπορούμε να διακρίνουμε τις περιπτώσεις για το πότε τα απόλυτα είναι θετικά ή αρνητικά και συνεχίσουμε την λύση. Ας δούμε έναν εναλλακτικό τρόπο για να προχωρήσουμε χωρίς να "ανοίξουμε" τα απόλυτα.
Στην ανίσωση μας ζητείται να συγκρίνουμε το γινόμενο δυο αριθμών με το μηδέν, οπότε με την αλλαγή κάθε παράγοντα με μια έκφραση του ίδου προσήμου προκύπτει ισοδύναμη ανίσωση. Παρατηρούμε ότι για τους μη αρνητικούς αριθμούς και
και  το πρόσημο της διαφοράς
το πρόσημο της διαφοράς  συμπίπτει με το πρόσημο της διαφοράς των τετραγώνων τους
συμπίπτει με το πρόσημο της διαφοράς των τετραγώνων τους  . Επομένως προκύπτει
. Επομένως προκύπτει





Η τελευταία ισοδυναμία ισχύει επειδή και
και  .
.
Από εδώ και πέρα συνεχίζουμε με την επίλυση των εξισώσεων και την κατάστρωση του πίνακα προσήμων.
παρατηρούμε ότι η ανίσωση γράφεται
 .
.

 .
.Θέτουμε
 , τότε η ανίσωση γράφεται
, τότε η ανίσωση γράφεται και την οποία μελετάμε σαν δευτεροβάθμιο τριώνυμο. Οι ρίζες της εξίσωσης
και την οποία μελετάμε σαν δευτεροβάθμιο τριώνυμο. Οι ρίζες της εξίσωσης  είναι
είναι και
και  . Έτσι η ανίσωση παίρνει την μορφή
. Έτσι η ανίσωση παίρνει την μορφή .
.Στην τελαυταία, παραγοντοποιημένη πλέον, ανίσωση μπορούμε να διακρίνουμε τις περιπτώσεις για το πότε τα απόλυτα είναι θετικά ή αρνητικά και συνεχίσουμε την λύση. Ας δούμε έναν εναλλακτικό τρόπο για να προχωρήσουμε χωρίς να "ανοίξουμε" τα απόλυτα.
Στην ανίσωση μας ζητείται να συγκρίνουμε το γινόμενο δυο αριθμών με το μηδέν, οπότε με την αλλαγή κάθε παράγοντα με μια έκφραση του ίδου προσήμου προκύπτει ισοδύναμη ανίσωση. Παρατηρούμε ότι για τους μη αρνητικούς αριθμούς
 και
και  το πρόσημο της διαφοράς
το πρόσημο της διαφοράς  συμπίπτει με το πρόσημο της διαφοράς των τετραγώνων τους
συμπίπτει με το πρόσημο της διαφοράς των τετραγώνων τους  . Επομένως προκύπτει
. Επομένως προκύπτει




Η τελευταία ισοδυναμία ισχύει επειδή
 και
και  .
.Από εδώ και πέρα συνεχίζουμε με την επίλυση των εξισώσεων και την κατάστρωση του πίνακα προσήμων.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες

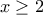 και
και  και έχω:
και έχω:

 Απ' όπου παίρνω
Απ' όπου παίρνω ή
ή  ή
ή 
![\boxed{x \in ( - \infty , - 2] \cup \left[ { - \frac{1}{4}\left( {\sqrt {17} + 1} \right),\frac{1}{4}\left( {\sqrt {17} - 1} \right)} \right] \cup [1, + \infty )} \boxed{x \in ( - \infty , - 2] \cup \left[ { - \frac{1}{4}\left( {\sqrt {17} + 1} \right),\frac{1}{4}\left( {\sqrt {17} - 1} \right)} \right] \cup [1, + \infty )}](/forum/ext/geomar/texintegr/latexrender/pictures/10ca2412a87f1a51121fe42ba6c7e38d.png)