Το θυμάμαι Μιχάλη, το πρόβλημα που τότε είχε δημιουργηθεί.
Οι μαθητές τα τελευταία χρόνια δεν διδάσκονται την ΜΑΘΗΜΑΤΙΚΗ ΛΟΓΙΚΗ, οπότε αν κάποιος είχε την ιδέα να θέσει
στην θέση του

κάτι άλλο, όπως συχνά κάνουμε σε τέτοιου είδους ασκήσεις , τότε θα διαπίστωνε ότι δεν είναι
δυνατόν να υπάρχει τέτοια συνάρτηση και είναι πολύ φυσιολογικό να σκεφτεί ότι τους έχει δοθεί λάθος άσκηση.
Το ερώτημα που είχε τεθεί τότε, ήταν: Τι μονάδες θα έπαιρνε ο συγκεκριμένος μαθητής; Είχαν δοθεί πολλές μάχες
για την απάντηση σε αυτό το ερώτημα.
Ας δούμε τώρα μια πιθανή αντιμετώπιση του θέματος που θα είχε κάνει κάποιος υποψήφιος: (αντί του

, έχουμε το

,
που δεν αλλάζει κάτι στην διαδικασία), (τυχαία η πορεία, σίγουρα υπάρχουν και συντομότερες αν το ψάξουμε)
Θέτουμε

και βρίσκουμε
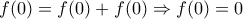
Θέτουμε τώρα όπου
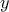
το
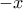
και έχουμε:
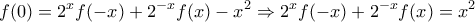
, (Α) , και θέτοντας

σε αυτήν, έχουμε:
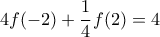
, (1)
Στη συνέχεια θέτουμε στην αρχική όπου
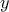
το
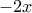
και παίρνουμε:
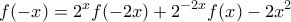
, και έτσι η (Α), γράφεται:
![\displaystyle{2^x . [2^x f(-2x)+2^{-2x} f(x) -2x^2 ]+2^{-x} f(x) = x^2 \Rightarrow 2^{2x}f(-2x) +2^{-x}f(x) -2^{x+1}.x^2 +2^{-x}f(x)=x^2 \Rightarrow} \displaystyle{2^x . [2^x f(-2x)+2^{-2x} f(x) -2x^2 ]+2^{-x} f(x) = x^2 \Rightarrow 2^{2x}f(-2x) +2^{-x}f(x) -2^{x+1}.x^2 +2^{-x}f(x)=x^2 \Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/451fd10049a38b5ef8678a43d7150df1.png)
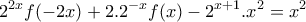
, και θέτοντας

σε αυτήν, παίρνουμε:
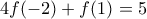
, (2).
Τέλος, θέτοντας στην αρχική

, παίρνουμε:
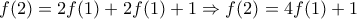
, οπότε λόγω αυτής, η (1) γράφεται:
![\displaystyle{4f(-2) +\frac{1}{4} .[4f(1)+1]=4 \Rightarrow 4f(-2)+f(1) +\frac{1}{4}=4\Rightarrow 4f(-2)+f(1)=\frac{15}{4}} \displaystyle{4f(-2) +\frac{1}{4} .[4f(1)+1]=4 \Rightarrow 4f(-2)+f(1) +\frac{1}{4}=4\Rightarrow 4f(-2)+f(1)=\frac{15}{4}}](/forum/ext/geomar/texintegr/latexrender/pictures/ed2056790232adbdd48106a243ddd978.png)
.
Η σχέση αυτή που καταλήξαμε σε συνδυασμό με την (2) καταλήγουν σε άτοπο, άρα τέτοια συνάρτηση δεν υπάρχει.
με
, για κάθε
.
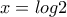 . Τότε
. Τότε 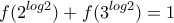 , (1)
, (1)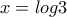 . Τότε:
. Τότε:  , (2)
, (2)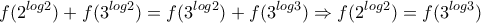
 είναι
είναι  , παίρνουμε
, παίρνουμε 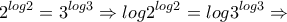
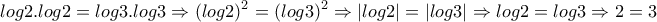

 έχουμε
έχουμε 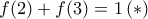 .
.  τέτοιο ώστε
τέτοιο ώστε 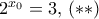 . Tότε για
. Tότε για  παίρνουμε
παίρνουμε 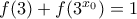 που με σύγκριση με την
που με σύγκριση με την  δίνει
δίνει 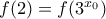 .
.  συνάρτηση
συνάρτηση  δίνει
δίνει 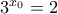 , οπότε από την
, οπότε από την  έχουμε
έχουμε 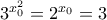 , και άρα
, και άρα  . Aυτό όμως αντιβαίνει στην
. Aυτό όμως αντιβαίνει στην  κάτι άλλο, όπως συχνά κάνουμε σε τέτοιου είδους ασκήσεις , τότε θα διαπίστωνε ότι δεν είναι
κάτι άλλο, όπως συχνά κάνουμε σε τέτοιου είδους ασκήσεις , τότε θα διαπίστωνε ότι δεν είναι , έχουμε το
, έχουμε το  ,
, και βρίσκουμε
και βρίσκουμε 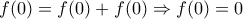
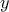 το
το 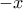 και έχουμε:
και έχουμε: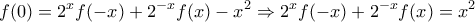 , (Α) , και θέτοντας
, (Α) , και θέτοντας  σε αυτήν, έχουμε:
σε αυτήν, έχουμε: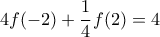 , (1)
, (1)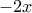 και παίρνουμε:
και παίρνουμε: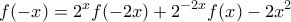 , και έτσι η (Α), γράφεται:
, και έτσι η (Α), γράφεται:![\displaystyle{2^x . [2^x f(-2x)+2^{-2x} f(x) -2x^2 ]+2^{-x} f(x) = x^2 \Rightarrow 2^{2x}f(-2x) +2^{-x}f(x) -2^{x+1}.x^2 +2^{-x}f(x)=x^2 \Rightarrow} \displaystyle{2^x . [2^x f(-2x)+2^{-2x} f(x) -2x^2 ]+2^{-x} f(x) = x^2 \Rightarrow 2^{2x}f(-2x) +2^{-x}f(x) -2^{x+1}.x^2 +2^{-x}f(x)=x^2 \Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/451fd10049a38b5ef8678a43d7150df1.png)
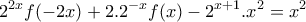 , και θέτοντας
, και θέτοντας  σε αυτήν, παίρνουμε:
σε αυτήν, παίρνουμε: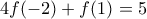 , (2).
, (2). , παίρνουμε:
, παίρνουμε: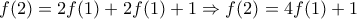 , οπότε λόγω αυτής, η (1) γράφεται:
, οπότε λόγω αυτής, η (1) γράφεται:![\displaystyle{4f(-2) +\frac{1}{4} .[4f(1)+1]=4 \Rightarrow 4f(-2)+f(1) +\frac{1}{4}=4\Rightarrow 4f(-2)+f(1)=\frac{15}{4}} \displaystyle{4f(-2) +\frac{1}{4} .[4f(1)+1]=4 \Rightarrow 4f(-2)+f(1) +\frac{1}{4}=4\Rightarrow 4f(-2)+f(1)=\frac{15}{4}}](/forum/ext/geomar/texintegr/latexrender/pictures/ed2056790232adbdd48106a243ddd978.png) .
.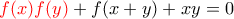 , για κάθε
, για κάθε 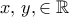
 που είχα, το σωστό είναι
που είχα, το σωστό είναι  .
. 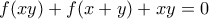 , για κάθε
, για κάθε  και
και  ελεύθερο παίρνουμε ότι η
ελεύθερο παίρνουμε ότι η  θέτοντας
θέτοντας  ).
). τη δοσμένη συνθήκη. Έστω προς άτοπο ότι υπάρχει τέτοια
τη δοσμένη συνθήκη. Έστω προς άτοπο ότι υπάρχει τέτοια 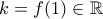 .
.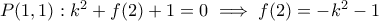
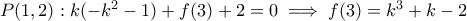
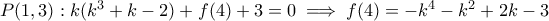
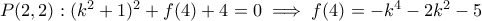
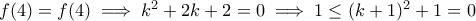 , άτοπο.
, άτοπο.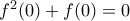 , οπότε
, οπότε 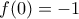 . Θα αποκλείσουμε και τα δύο.
. Θα αποκλείσουμε και τα δύο. 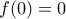 τότε το
τότε το 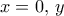 ελεύθερο δίνει
ελεύθερο δίνει  , που όμως απορρίπτεται αφού η μηδενική συνάρτηση δεν ικανοποιεί την σχέση. Μένει η
, που όμως απορρίπτεται αφού η μηδενική συνάρτηση δεν ικανοποιεί την σχέση. Μένει η 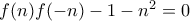 και ειδικά
και ειδικά 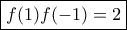 και
και 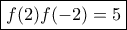 .
. 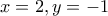 και
και 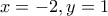 παίρνουμε αντίστοιχα
παίρνουμε αντίστοιχα 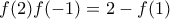 και
και 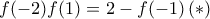 . Πολλαπλασιάζοντας κατά μέλη έχουμε
. Πολλαπλασιάζοντας κατά μέλη έχουμε ![[f(2)f(-2)][f(1)f(-1)]= (2-f(1))(2-f(-1)) = 4 -2(f(1)+f(-1)) + f(1)f(-1) [f(2)f(-2)][f(1)f(-1)]= (2-f(1))(2-f(-1)) = 4 -2(f(1)+f(-1)) + f(1)f(-1)](/forum/ext/geomar/texintegr/latexrender/pictures/f5ba732b0ebac2c5f105edb7bedb2048.png) που από τις
που από τις 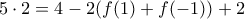 οπότε
οπότε 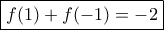 .
. 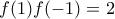 μας λέει ότι τα
μας λέει ότι τα 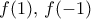 είναι ρίζες της
είναι ρίζες της 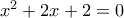 , που όμως δεν έχει πραγματικές ρίζες. Και λοιπά.
, που όμως δεν έχει πραγματικές ρίζες. Και λοιπά.