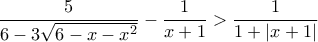 .
.Ρητή ανίσωση με απόλυτο
Συντονιστής: exdx
- Al.Koutsouridis
- Δημοσιεύσεις: 1930
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ρητή ανίσωση με απόλυτο
Θέτοντας τους απαραίτητους περιορισμούς:
![\displaystyle{
\left\{
\begin{aligned}
&x + 1 \ne 0 \\[0.05in]
&6 - 3\sqrt{6 - x - x^2} \ne 0 \\[0.05in]
&6 - x - x^2 \ge 0
\end{aligned}
\right.
\Leftrightarrow
\left\{
\begin{aligned}
&x \ne -1 \\[0.05in]
&x^2 + x - 2 \ne 0 \\[0.05in]
&x \in [-3, 2]
\end{aligned}
\right.
\Leftrightarrow \boxed{x \in \bigl[-3, 2 \bigr] - \bigl\{ -2, -1, 1\bigr\}}
} \displaystyle{
\left\{
\begin{aligned}
&x + 1 \ne 0 \\[0.05in]
&6 - 3\sqrt{6 - x - x^2} \ne 0 \\[0.05in]
&6 - x - x^2 \ge 0
\end{aligned}
\right.
\Leftrightarrow
\left\{
\begin{aligned}
&x \ne -1 \\[0.05in]
&x^2 + x - 2 \ne 0 \\[0.05in]
&x \in [-3, 2]
\end{aligned}
\right.
\Leftrightarrow \boxed{x \in \bigl[-3, 2 \bigr] - \bigl\{ -2, -1, 1\bigr\}}
}](/forum/ext/geomar/texintegr/latexrender/pictures/691e4ba416dbb023aa82eaf6f0bcd060.png)
ισοδύναμα γράφω:
![\displaystyle{
\begin{aligned}
\dfrac{5}{6 - 3\sqrt{6 - x - x^2}} - \dfrac{1}{x + 1} > \dfrac{1}{1 + |x + 1|}
&\Leftrightarrow \dfrac{5 \Bigl(6 + 3\sqrt{6 - x - x^2} \Bigr)}{36 - 54 + 9x + 9x^2} > \dfrac{1}{1 + |x + 1|} + \dfrac{1}{x + 1}
\\[0.1in]
&\Leftrightarrow \dfrac{5}{3} \cdot \dfrac{2 + \sqrt{6 - x - x^2}}{x^2 + x - 2} > \dfrac{1}{1 + |x + 1|} + \dfrac{1}{x + 1}
\\[0.1in]
&\Leftrightarrow \dfrac{5}{3} \cdot \dfrac{2 + \sqrt{(2 - x)(x + 3)}}{(x + 2)(x - 1)} > \dfrac{1}{1 + |x + 1|} + \dfrac{1}{x + 1} \quad (1)
\end{aligned}
} \displaystyle{
\begin{aligned}
\dfrac{5}{6 - 3\sqrt{6 - x - x^2}} - \dfrac{1}{x + 1} > \dfrac{1}{1 + |x + 1|}
&\Leftrightarrow \dfrac{5 \Bigl(6 + 3\sqrt{6 - x - x^2} \Bigr)}{36 - 54 + 9x + 9x^2} > \dfrac{1}{1 + |x + 1|} + \dfrac{1}{x + 1}
\\[0.1in]
&\Leftrightarrow \dfrac{5}{3} \cdot \dfrac{2 + \sqrt{6 - x - x^2}}{x^2 + x - 2} > \dfrac{1}{1 + |x + 1|} + \dfrac{1}{x + 1}
\\[0.1in]
&\Leftrightarrow \dfrac{5}{3} \cdot \dfrac{2 + \sqrt{(2 - x)(x + 3)}}{(x + 2)(x - 1)} > \dfrac{1}{1 + |x + 1|} + \dfrac{1}{x + 1} \quad (1)
\end{aligned}
}](/forum/ext/geomar/texintegr/latexrender/pictures/140f7e4e66185082a0ff067ef94daa40.png)
Διακρίνω περιπτώσεις:
- Για
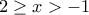 με
με 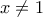 :
:
![\displaystyle{
\begin{aligned}
(1)
\Leftrightarrow
\dfrac{5}{3} \cdot \dfrac{2 + \sqrt{(2 - x)(x + 3)}}{(x + 2)(x - 1)} > \dfrac{1}{x +2} + \dfrac{1}{x + 1}
&\Leftrightarrow
\dfrac{5(x + 1) \Bigl[ 2 + \sqrt{(2 - x)(x + 3)} \Bigr]}{3(x + 2)(x - 1)(x + 1)} > \dfrac{6x^2 + 3x - 9}{3(x + 2)(x - 1)(x + 1)}
\\[0.1in]
&\Leftrightarrow
\dfrac{\overbrace{5(x + 1) \sqrt{(2 - x)(x + 3)} \;}^{\ge \; 0} \overbrace{- \; 6x^2 + 7x + 19}^{> \; 0 \text{ \textgreek{για} } x \; \in \; [-1, \; 2 \,] }}{3(x + 2)(x - 1)(x + 1)} > 0
\\[0.05in]
&\Leftrightarrow (x + 2)(x - 1)(x + 1) > 0
\\[0.05in]
&\Leftrightarrow \boxed{1 < x \le 2}
\end{aligned}
} \displaystyle{
\begin{aligned}
(1)
\Leftrightarrow
\dfrac{5}{3} \cdot \dfrac{2 + \sqrt{(2 - x)(x + 3)}}{(x + 2)(x - 1)} > \dfrac{1}{x +2} + \dfrac{1}{x + 1}
&\Leftrightarrow
\dfrac{5(x + 1) \Bigl[ 2 + \sqrt{(2 - x)(x + 3)} \Bigr]}{3(x + 2)(x - 1)(x + 1)} > \dfrac{6x^2 + 3x - 9}{3(x + 2)(x - 1)(x + 1)}
\\[0.1in]
&\Leftrightarrow
\dfrac{\overbrace{5(x + 1) \sqrt{(2 - x)(x + 3)} \;}^{\ge \; 0} \overbrace{- \; 6x^2 + 7x + 19}^{> \; 0 \text{ \textgreek{για} } x \; \in \; [-1, \; 2 \,] }}{3(x + 2)(x - 1)(x + 1)} > 0
\\[0.05in]
&\Leftrightarrow (x + 2)(x - 1)(x + 1) > 0
\\[0.05in]
&\Leftrightarrow \boxed{1 < x \le 2}
\end{aligned}
}](/forum/ext/geomar/texintegr/latexrender/pictures/f5085d16e76901505be472985724902e.png)
- Για
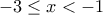 με
με 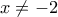 :
:
![\displaystyle{
\begin{aligned}
(1)
\Leftrightarrow
\dfrac{5}{3} \cdot \dfrac{2 + \sqrt{6 - x - x^2}}{(x - 1)(x + 2)} > \dfrac{1}{x + 1} - \dfrac{1}{x}
&\Leftrightarrow
\dfrac{ 5x(x + 1) \Bigl[2 + \sqrt{6 - x - x^2} \Bigr] }{3x(x + 1)(x + 2)(x - 1)} > - \dfrac{3x^2 + 3x - 6}{3x(x + 1)(x - 1)(x + 2)}
\\[0.15in]
&\Leftrightarrow
\dfrac{ 5x(x + 1) \Bigl[2 + \sqrt{6 - x(x + 1)} \Bigr] + 3x(x + 1) - 6 }{3x(x + 1)\bigl[ x(x + 1) - 2 \bigr]} > 0
\\[0.15in]
\overunderset{\ \ \ \ \ y \; := \; x(x \; + \; 1)}{\ \ \ \ y \; \in \; (0, 6], \ y \; \ne \; 2}{\Leftarrow\joinrel=\joinrel=\joinrel=\joinrel=\joinrel=\joinrel=\joinrel=\joinrel=\joinrel\joinrel\joinrel}&\joinrel\joinrel\!\Rightarrow
\dfrac{ 5y \Bigl( 2 + \sqrt{6 - y} \Bigr) + 3y - 6 }{3y(y - 2)} > 0
\\[0.15in]
&\Leftrightarrow
(y - 2) \Bigl( 5y \sqrt{6 - y} + 13y - 6 \Bigr) > 0
\end{aligned}
} \displaystyle{
\begin{aligned}
(1)
\Leftrightarrow
\dfrac{5}{3} \cdot \dfrac{2 + \sqrt{6 - x - x^2}}{(x - 1)(x + 2)} > \dfrac{1}{x + 1} - \dfrac{1}{x}
&\Leftrightarrow
\dfrac{ 5x(x + 1) \Bigl[2 + \sqrt{6 - x - x^2} \Bigr] }{3x(x + 1)(x + 2)(x - 1)} > - \dfrac{3x^2 + 3x - 6}{3x(x + 1)(x - 1)(x + 2)}
\\[0.15in]
&\Leftrightarrow
\dfrac{ 5x(x + 1) \Bigl[2 + \sqrt{6 - x(x + 1)} \Bigr] + 3x(x + 1) - 6 }{3x(x + 1)\bigl[ x(x + 1) - 2 \bigr]} > 0
\\[0.15in]
\overunderset{\ \ \ \ \ y \; := \; x(x \; + \; 1)}{\ \ \ \ y \; \in \; (0, 6], \ y \; \ne \; 2}{\Leftarrow\joinrel=\joinrel=\joinrel=\joinrel=\joinrel=\joinrel=\joinrel=\joinrel=\joinrel\joinrel\joinrel}&\joinrel\joinrel\!\Rightarrow
\dfrac{ 5y \Bigl( 2 + \sqrt{6 - y} \Bigr) + 3y - 6 }{3y(y - 2)} > 0
\\[0.15in]
&\Leftrightarrow
(y - 2) \Bigl( 5y \sqrt{6 - y} + 13y - 6 \Bigr) > 0
\end{aligned}
}](/forum/ext/geomar/texintegr/latexrender/pictures/21069b44b29f95c1019e04f173efb04e.png)
Βρίσκω τις τιμές του για τις οποίες η δεύτερη παρένθεση είναι θετική. Προφανώς, για
για τις οποίες η δεύτερη παρένθεση είναι θετική. Προφανώς, για 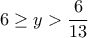 είναι θετική. Για
είναι θετική. Για 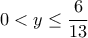 , τώρα, είναι:
, τώρα, είναι:
![\displaystyle{
\begin{aligned}
5y \sqrt{6 - y} + 13y - 6 > 0
\Leftrightarrow 5y \sqrt{6 - y} > 6 - 13y \ge 0
&\Leftrightarrow 150y^2 - 25y^3 > 169y^2 - 156y + 36
\\[0.05in]
&\Leftrightarrow
25y^3 + 19y^2 - 156y + 36 < 0
\\[0.05in]
\overset{\ \ \ \ \rm Horner}{\Leftarrow \joinrel=\joinrel=\joinrel=\joinrel=\joinrel\joinrel}\joinrel\joinrel&\Rightarrow
(y - 2)(y + 3)\biggl( y - \dfrac{6}{25} \biggr) < 0
\\[0.05in]
&\Leftrightarrow \boxed{\dfrac{6}{25} < y \le \dfrac{6}{13}}
\end{aligned}
} \displaystyle{
\begin{aligned}
5y \sqrt{6 - y} + 13y - 6 > 0
\Leftrightarrow 5y \sqrt{6 - y} > 6 - 13y \ge 0
&\Leftrightarrow 150y^2 - 25y^3 > 169y^2 - 156y + 36
\\[0.05in]
&\Leftrightarrow
25y^3 + 19y^2 - 156y + 36 < 0
\\[0.05in]
\overset{\ \ \ \ \rm Horner}{\Leftarrow \joinrel=\joinrel=\joinrel=\joinrel=\joinrel\joinrel}\joinrel\joinrel&\Rightarrow
(y - 2)(y + 3)\biggl( y - \dfrac{6}{25} \biggr) < 0
\\[0.05in]
&\Leftrightarrow \boxed{\dfrac{6}{25} < y \le \dfrac{6}{13}}
\end{aligned}
}](/forum/ext/geomar/texintegr/latexrender/pictures/92ea1512164c09a35987ce42e74c385e.png)
Τελικά - και συναληθεύοντας με τους περιορισμούς για το - η δεύτερη παρένθεση είναι θετική αν και μόνο αν:
- η δεύτερη παρένθεση είναι θετική αν και μόνο αν:
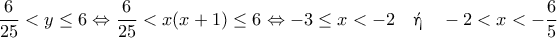
και προφανώς αρνητική αν και μόνο αν: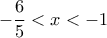 . Με πίνακα προσήμου, βρίσκω πως στο υπό εξέταση διάστημα η ανίσωση έχει λύση την:
. Με πίνακα προσήμου, βρίσκω πως στο υπό εξέταση διάστημα η ανίσωση έχει λύση την:  .
.
 για τα οποία ισχύει
για τα οποία ισχύει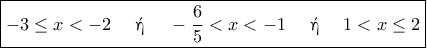
- Al.Koutsouridis
- Δημοσιεύσεις: 1930
- Εγγραφή: Πέμ Ιαν 30, 2014 11:58 pm
- Τοποθεσία: Αθήνα
Re: Ρητή ανίσωση με απόλυτο
Θα ήθελα να ευχαριστήσω τον vgreco για την λύση του στο παρόν πρόβλημα, αλλά και στα άλλα παρόμοια, που έλυσε πρόσφατα. Για την ιστορία η άσκηση είναι από τις εισαγωγικές εξετάσεις του Φυσικό-Τεχνολογικού Ινστιτούτου Μόσχας για το έτος 2004.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
