
Oλοκλήρωμα
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: Oλοκλήρωμα
Από τον κανόνα του Leibniz έχουμε
![f'(a)=-2 \int_{0}^{1}\frac{1}{(x-\cos a)^2 +\sin ^2 a}dx=\frac{-2}{\sin ^2 a}\int_{0}^{1}\frac{1}{1+(\frac{x- \cos a}{\sin a })^2}dx=\frac{-2}{\sin a}[\arctan \frac{x- \cos a }{\sin a}]_{0}^{1} f'(a)=-2 \int_{0}^{1}\frac{1}{(x-\cos a)^2 +\sin ^2 a}dx=\frac{-2}{\sin ^2 a}\int_{0}^{1}\frac{1}{1+(\frac{x- \cos a}{\sin a })^2}dx=\frac{-2}{\sin a}[\arctan \frac{x- \cos a }{\sin a}]_{0}^{1}](/forum/ext/geomar/texintegr/latexrender/pictures/22753f166985bf2b214a6abd14c067e4.png)
Όμως και
και  και βρίσκουμε τελικά
και βρίσκουμε τελικά
 ooooops.
ooooops.
Y.Γ. Δουλειά του ποδαριού

![f'(a)=-2 \int_{0}^{1}\frac{1}{(x-\cos a)^2 +\sin ^2 a}dx=\frac{-2}{\sin ^2 a}\int_{0}^{1}\frac{1}{1+(\frac{x- \cos a}{\sin a })^2}dx=\frac{-2}{\sin a}[\arctan \frac{x- \cos a }{\sin a}]_{0}^{1} f'(a)=-2 \int_{0}^{1}\frac{1}{(x-\cos a)^2 +\sin ^2 a}dx=\frac{-2}{\sin ^2 a}\int_{0}^{1}\frac{1}{1+(\frac{x- \cos a}{\sin a })^2}dx=\frac{-2}{\sin a}[\arctan \frac{x- \cos a }{\sin a}]_{0}^{1}](/forum/ext/geomar/texintegr/latexrender/pictures/22753f166985bf2b214a6abd14c067e4.png)
Όμως
 και
και  και βρίσκουμε τελικά
και βρίσκουμε τελικά  ooooops.
ooooops.Y.Γ. Δουλειά του ποδαριού

Μάγκος Θάνος
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Oλοκλήρωμα
Ελπίζω να μην έχω λάθος. Για 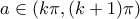 με
με  από Leibnitz έχουμε
από Leibnitz έχουμε
 , άρα
, άρα
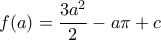 .
.
Όμως .
.
Αλλά . Συνεπώς
. Συνεπώς
 , άρα
, άρα
 και συνεπώς
και συνεπώς 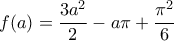 για
για 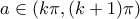
Για έχουμε παρόμοια ότι
έχουμε παρόμοια ότι  και
και
γγια ότι
ότι  .
.
Υ.Γ. Γρηγόρη σε ευχαριστώ. Τώρα για το άλλο λαθάκι...ο θεός και η ψυχή μου
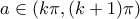 με
με  από Leibnitz έχουμε
από Leibnitz έχουμε  , άρα
, άρα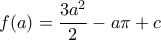 .
. Όμως
 .
.Αλλά
 . Συνεπώς
. Συνεπώς , άρα
, άρα και συνεπώς
και συνεπώς 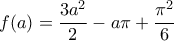 για
για 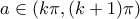
Για
 έχουμε παρόμοια ότι
έχουμε παρόμοια ότι  και
καιγγια
 ότι
ότι  .
.Υ.Γ. Γρηγόρη σε ευχαριστώ. Τώρα για το άλλο λαθάκι...ο θεός και η ψυχή μου
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Παρ Μάιος 28, 2010 12:08 am, έχει επεξεργασθεί 1 φορά συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης

