
Όρια με ολοκληρώματα
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Re: Όρια με ολοκληρώματα
27) και φρενάρω για την ώρα 


Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: Όρια με ολοκληρώματα
Τι ψεύτης Θεέ μου...mathxl έγραψε:27) και φρενάρω για την ώρα
28) Να δείξετε ότι
![\displaystyle{\mathop {\lim }\limits_{n \to \infty } {n^2}\left( {\int_0^1 {\sqrt[n]{{1 + {x^n}}}} dx - 1} \right) = \frac{{{\pi ^2}}}{{12}}.} \displaystyle{\mathop {\lim }\limits_{n \to \infty } {n^2}\left( {\int_0^1 {\sqrt[n]{{1 + {x^n}}}} dx - 1} \right) = \frac{{{\pi ^2}}}{{12}}.}](/forum/ext/geomar/texintegr/latexrender/pictures/87398e84d1a0bf183605a466a3637ab3.png)
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Όρια με ολοκληρώματα
mathxl έγραψε:24)
Έστω η συνεχής συνάρτηση. Αν α > 0 και
να
ι) δείξετε ότι η F είναι παραγωγίσιμη στο (0,1)
ιι) υπολογίσετε το
ιιι) υπολογίσετε το
 Η παραγωγισιμότητα της
Η παραγωγισιμότητα της  προκύπτει από τον κανόνα του Leibnitz και ισχύει στο
προκύπτει από τον κανόνα του Leibnitz και ισχύει στο  , με
, με 
Παρατηρούμε ότι οι
 είναι φραγμένες στο
είναι φραγμένες στο ![\displaystyle{[0,1]} \displaystyle{[0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/1109a14ceae9f7dfdce6cfbb76246020.png) . Από τη συνέχεια τώρα της
. Από τη συνέχεια τώρα της  στο
στο  , προκύπτει εύκολα ότι
, προκύπτει εύκολα ότι  και
και  στο
στο ![\displaystyle{[0,1]} \displaystyle{[0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/1109a14ceae9f7dfdce6cfbb76246020.png) καθώς
καθώς  .
. 
Τώρα έχουμε :

 .
.********************************************************************************
Για το
 , δεν ξέρω αν μπορεί να χρησιμοποιηθεί το πρώτο, η λύση μου όμως είναι η εξής :
, δεν ξέρω αν μπορεί να χρησιμοποιηθεί το πρώτο, η λύση μου όμως είναι η εξής : Θέτω
![\displaystyle{M=\max_{x\in[0,1]}f(x)} \displaystyle{M=\max_{x\in[0,1]}f(x)}](/forum/ext/geomar/texintegr/latexrender/pictures/5617acb9a49331b4712ba7fbfa11e042.png) .
.Έστω
 . Από τη συνέχεια της
. Από τη συνέχεια της  βρίσκω
βρίσκω ![\displaystyle{[c,d]\subseteq[0,1]} \displaystyle{[c,d]\subseteq[0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/1288d3e61cfadc07c5c55cc5e87390a0.png) με
με ![\displaystyle{M\geq f(x)\geq M-h>0\,\,\forall x\in[c,d]} \displaystyle{M\geq f(x)\geq M-h>0\,\,\forall x\in[c,d]}](/forum/ext/geomar/texintegr/latexrender/pictures/f06248578ff1074c03b0e7a39fcb1e2f.png) ,
, άρα και
![\displaystyle{f^{a}(x)\geq (M-h)^{a}>0\,\,\forall x\in[c,d]\quad\boxed{*}} \displaystyle{f^{a}(x)\geq (M-h)^{a}>0\,\,\forall x\in[c,d]\quad\boxed{*}}](/forum/ext/geomar/texintegr/latexrender/pictures/a1926493f09dddfd302a02f272ee42ce.png) .
.Επειδή
 , βρίσκω και
, βρίσκω και  με
με  .
.Τώρα
 ,
,άρα το όριο είναι
 .
.******************************************************************
Να συμπληρώσω ότι ισχύει και ότι
 , όπου
, όπου ![\displaystyle{m:=\min_{x\in[0,1]}f(x)} \displaystyle{m:=\min_{x\in[0,1]}f(x)}](/forum/ext/geomar/texintegr/latexrender/pictures/c2fc1f1c6eed558bf9cc1ecf5ed9f112.png) .
.Απόδειξη :
![\displaystyle{\lim_{a\to-\infty}\big(F(a)\big)^{1/a}\stackrel{y=-a}{=}\lim_{y\to+\infty}\Big(\int_{0}^{1}f^{-y}(x)\,dx\Big)^{-1/y}=\lim_{y\to+\infty}\frac{1}{\displaystyle\Big(\int_{0}^{1}\Big(\frac{1}{f(x)}\Big)^{y}\,dx\Big)^{1/y}}\stackrel{ii)}{\longrightarrow}1/\max_{x\in[0,1]}1/f(x)\stackrel{\boxed{*}}{=}\min_{x\in[0,1]}f(x)} \displaystyle{\lim_{a\to-\infty}\big(F(a)\big)^{1/a}\stackrel{y=-a}{=}\lim_{y\to+\infty}\Big(\int_{0}^{1}f^{-y}(x)\,dx\Big)^{-1/y}=\lim_{y\to+\infty}\frac{1}{\displaystyle\Big(\int_{0}^{1}\Big(\frac{1}{f(x)}\Big)^{y}\,dx\Big)^{1/y}}\stackrel{ii)}{\longrightarrow}1/\max_{x\in[0,1]}1/f(x)\stackrel{\boxed{*}}{=}\min_{x\in[0,1]}f(x)}](/forum/ext/geomar/texintegr/latexrender/pictures/9b258610add4ab15ed966790d1004591.png) .
.
![\displaystyle{M_{1/f}:=\max_{x\in[0,1]}1/f(x)\Rightarrow\forall x\in[0,1]: 1/f(x)\leq M_{1/f}\Rightarrow\forall x\in[0,1]: f(x)\geq1/M_{1/f}\Rightarrow1/M_{1/f}=m_{f}} \displaystyle{M_{1/f}:=\max_{x\in[0,1]}1/f(x)\Rightarrow\forall x\in[0,1]: 1/f(x)\leq M_{1/f}\Rightarrow\forall x\in[0,1]: f(x)\geq1/M_{1/f}\Rightarrow1/M_{1/f}=m_{f}}](/forum/ext/geomar/texintegr/latexrender/pictures/889c2c08964dc4c53e6e63c99a0d4ff7.png) (με τις αντίχτοιχες ισότητες φυσικά να "πιάνονται").
(με τις αντίχτοιχες ισότητες φυσικά να "πιάνονται").*********************************************************************
Το αντίστοιχο διακριτό ανάλογο των παραπάνω είναι το εξής :
Έστω
 θετικοί πραγματικοί και
θετικοί πραγματικοί και  .
. Αν
 , θέτουμε
, θέτουμε 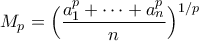 και
και 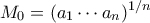 . Δείξτε ότι
. Δείξτε ότι
 ,
,

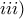
 και
και

(Νεγρεπόντης ΙΙα σ.155 ασκ 21.100)
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Πέμ Ιουν 10, 2010 1:27 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
Re: Όρια με ολοκληρώματα
Η παραπάνω άσκηση είναι από  και δεν είχε λύση από εκεί που την πήρα
και δεν είχε λύση από εκεί που την πήρα
 και δεν είχε λύση από εκεί που την πήρα
και δεν είχε λύση από εκεί που την πήραΠοτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Όρια με ολοκληρώματα
Ας δούμε και μια παρόμοια με την 
 Έστω
Έστω ![\displaystyle{f[a,b]\to\mathbb{R}} \displaystyle{f[a,b]\to\mathbb{R}}](/forum/ext/geomar/texintegr/latexrender/pictures/0781d93eb2f6c28ec3f61bb3100f1cfc.png) (
( για τα
για τα  ) ολοκληρώσιμη.
) ολοκληρώσιμη.
Θέτουμε με
με  . Τότε :
. Τότε :

 ,
,

![\displaystyle{\lim_{n\to+\infty}\sqrt[n]{f_{1n}\cdots f_{nn}}=e^{\frac{1}{b-a}\int_{a}^{b}\ln(f(x))\,dx}} \displaystyle{\lim_{n\to+\infty}\sqrt[n]{f_{1n}\cdots f_{nn}}=e^{\frac{1}{b-a}\int_{a}^{b}\ln(f(x))\,dx}}](/forum/ext/geomar/texintegr/latexrender/pictures/198dda0be7b47b2a7761660287c4bf28.png) , και
, και
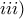

Υ.Γ.: Γενικεύεται και στα γενικευμένα ολοκληρώματα

 Έστω
Έστω ![\displaystyle{f[a,b]\to\mathbb{R}} \displaystyle{f[a,b]\to\mathbb{R}}](/forum/ext/geomar/texintegr/latexrender/pictures/0781d93eb2f6c28ec3f61bb3100f1cfc.png) (
( για τα
για τα  ) ολοκληρώσιμη.
) ολοκληρώσιμη. Θέτουμε
 με
με  . Τότε :
. Τότε : 
 ,
,
![\displaystyle{\lim_{n\to+\infty}\sqrt[n]{f_{1n}\cdots f_{nn}}=e^{\frac{1}{b-a}\int_{a}^{b}\ln(f(x))\,dx}} \displaystyle{\lim_{n\to+\infty}\sqrt[n]{f_{1n}\cdots f_{nn}}=e^{\frac{1}{b-a}\int_{a}^{b}\ln(f(x))\,dx}}](/forum/ext/geomar/texintegr/latexrender/pictures/198dda0be7b47b2a7761660287c4bf28.png) , και
, και 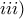

Υ.Γ.: Γενικεύεται και στα γενικευμένα ολοκληρώματα
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Τρί Οκτ 05, 2010 1:28 pm, έχει επεξεργασθεί 3 φορές συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Όρια με ολοκληρώματα
Μια γενίκευση της 
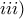 υπάρχει εδώ με τη μόνη διαφορά ότι εδώ η μεταβλητή ως προς την οποίια παίρνουμε όριο είναι συνεχής
υπάρχει εδώ με τη μόνη διαφορά ότι εδώ η μεταβλητή ως προς την οποίια παίρνουμε όριο είναι συνεχής

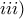 υπάρχει εδώ με τη μόνη διαφορά ότι εδώ η μεταβλητή ως προς την οποίια παίρνουμε όριο είναι συνεχής
υπάρχει εδώ με τη μόνη διαφορά ότι εδώ η μεταβλητή ως προς την οποίια παίρνουμε όριο είναι συνεχής
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Τρί Οκτ 05, 2010 1:28 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
Re: Όρια με ολοκληρώματα
Τάσο έχω ήδη δώσει μία για 28 , αν βάλουμε 29 την δική σου τότε η ακόλουθη είναι η
30) Να προσδιορίσετε τον πραγματικ'ό αριθμό α ώστε
με
Για την τιμή του α που βρήκατε να υπολογίσετε και το όριο L
30) Να προσδιορίσετε τον πραγματικ'ό αριθμό α ώστε

με

Για την τιμή του α που βρήκατε να υπολογίσετε και το όριο L
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Όρια με ολοκληρώματα
mathxl έγραψε:27) και φρενάρω για την ώρα


Εσύ....; Θα γίνεις κανίβαλος....;
Re: Όρια με ολοκληρώματα
Την ίδια λύση έχω δει και εγώ η οποία βασίζεται στην σειρά 
χωρίς αλλαγή μεταβλητής



Με τέτοιο τρόπο βγαίνει
;;; (Αλλαγή σειράς ολοκλήρωσης);

χωρίς αλλαγή μεταβλητής



Με τέτοιο τρόπο βγαίνει

;;; (Αλλαγή σειράς ολοκλήρωσης);
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Όρια με ολοκληρώματα
Πάρα πολύ μου άρεσε αυτό!mathxl έγραψε:Τι ψεύτης Θεέ μου...
28) Να δείξετε ότι
Λοιπόν:
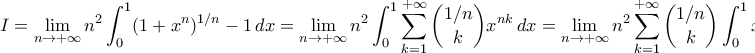


 (εναλλαγή ορίων)
(εναλλαγή ορίων) (για σταθερό
(για σταθερό  έχουμε πηλίκο πολυωνύμων του
έχουμε πηλίκο πολυωνύμων του  ίδιου βαθμού
ίδιου βαθμού  )
) ,
,Με την εναλλαγή των ορίων να δικαιολογείται λόγω απόλυτης σύγκλισης.
Εσύ....; Θα γίνεις κανίβαλος....;
Re: Όρια με ολοκληρώματα
Τάσο το θέμα είναι από Vojtech Jarnik, 2002, Categoria II και είνα αναπάντητο από εκεί που το πήρα
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Όρια με ολοκληρώματα
Αυτές οι ονομασίες που δίνεις είναι forums;mathxl έγραψε:Τάσο το θέμα είναι από Vojtech Jarnik, 2002, Categoria II και είνα αναπάντητο από εκεί που το πήρα
Εσύ....; Θα γίνεις κανίβαλος....;
Re: Όρια με ολοκληρώματα
Διαγωνισμοί πρέπει να είναι που βρίσκω από φόρουμ
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: Όρια με ολοκληρώματα
31) Ας δούμε (ένα γράμμα πιο αριστερά στο πληκτρολόγιο Φωτεινή  -όπως καταλαβαίνεις, δεν κοιτώ τι γράφω
-όπως καταλαβαίνεις, δεν κοιτώ τι γράφω  ) και αυτό το όριο
) και αυτό το όριο


Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: Όρια με ολοκληρώματα
Είναι τα λεγόμενα Fresnel integrals !
To αποτέλεσμα είναι
Από ότι θυμάμαι όμως δεν είναι και πολύ εύκολο στον υπολογισμό!
To αποτέλεσμα είναι

Από ότι θυμάμαι όμως δεν είναι και πολύ εύκολο στον υπολογισμό!
Σιλουανός Μπραζιτίκος
- chris_gatos
- Επιμελητής
- Δημοσιεύσεις: 6962
- Εγγραφή: Κυρ Δεκ 21, 2008 9:03 pm
- Τοποθεσία: Ανθούπολη
Re: Όρια με ολοκληρώματα
Δες και εδώ.Από ότι θυμάμαι όμως δεν είναι και πολύ εύκολο στον υπολογισμό!
What's wrong with a Greek in Hamburg?
Re: Όρια με ολοκληρώματα
Αυτό ήθελα Γιώργο, ευχαριστώΩmega Man έγραψε:Δες και εδώ.Από ότι θυμάμαι όμως δεν είναι και πολύ εύκολο στον υπολογισμό!
Δίνω και μια άλλη λύση που βρήκα με Γ και διπλό ολοκλήρωμα εδώ http://www.artofproblemsolving.com/Foru ... +integrals
ο κόλπο ακόμη πιο γρήγορα και όμορφα εδώ http://www.mathhelpforum.com/math-help/ ... ost44.html
Καλορίζικοι οι επιμελητές μας
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Όρια με ολοκληρώματα
Με διπλό ολοκλήρωμα και εναλλαγή σειράς άθροισης (χωρίς μιγαδική ανάλυση) υπάρχει και στο βιβλίο του Nowak Problems in mathematical analysis III p.191
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Παρ Ιουν 11, 2010 7:03 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Όρια με ολοκληρώματα
Είναι συγκεκριμένα το πρόβλημα 4 του 2002 της κατηγορίας 2 εδώ.mathxl έγραψε:28) Να δείξετε ότι
Εσύ....; Θα γίνεις κανίβαλος....;
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες




![\displaystyle{I=\mathop {\lim }\limits_{n \to \infty } {n^2}\left( {\int_0^1 {\sqrt[n]{{1 + {x^n}}}} dx - 1} \right) = \frac{{{\pi ^2}}}{{12}}.} \displaystyle{I=\mathop {\lim }\limits_{n \to \infty } {n^2}\left( {\int_0^1 {\sqrt[n]{{1 + {x^n}}}} dx - 1} \right) = \frac{{{\pi ^2}}}{{12}}.}](/forum/ext/geomar/texintegr/latexrender/pictures/58453be6abc90b626d42fa2b305c2bff.png)