Να βρεθούν οι συνεχείς συναρτήσεις
 , για τις οποίες υπάρχει συνάρτηση
, για τις οποίες υπάρχει συνάρτηση  , 1-1, ώστε
, 1-1, ώστε 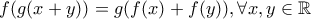
Φιλικά
Συντονιστής: emouroukos
 , για τις οποίες υπάρχει συνάρτηση
, για τις οποίες υπάρχει συνάρτηση  , 1-1, ώστε
, 1-1, ώστε 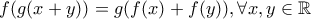
Δηλαδή Ανδρέα ισχυρίζεσαι ότι ηΑνδρέας Πούλος έγραψε:...
Από την (3) προκύπτει ότι όλες οι σταθερές συναρτήσεις και όλες οι συνεχείς και περιττές συναρτήσεις είναι λύσεις της συναρτησιακής μας εξίσωσης.
Ισχυρίζομαι ότι δεν υπάρχουν άλλες συναρτήσεις που είναι λύσεις της δεδομένης εξίσωσης.
Ες αύριον τα σπουδαία.
Φιλικά,
Ανδρέας Πούλος
 είναι λύση του προβλήματος; Δεν νομίζω
είναι λύση του προβλήματος; Δεν νομίζω , τότε η δοθείσα για
, τότε η δοθείσα για  , δίνει
, δίνει  , άρα επειδή είναι συνεχής (Cauchy)
, άρα επειδή είναι συνεχής (Cauchy) 
 . Τοτε εχουμε
. Τοτε εχουμε ![f[g(x+y)] = f[g(2u)] f[g(x+y)] = f[g(2u)]](/forum/ext/geomar/texintegr/latexrender/pictures/be6a7c7814c0fb6949ef896bcefc57d6.png) , δηλαδη
, δηλαδη ![g[f(x) + f(y)] = g[2 f(u)] g[f(x) + f(y)] = g[2 f(u)]](/forum/ext/geomar/texintegr/latexrender/pictures/86121afcca16ac26aa97433db7f5cc66.png) και
και  απο το 1-1 της
απο το 1-1 της  .
. , ισχυει οτι το μεσο του ευθυγραμμου τμηματος που οριζουν ειναι επισης σημειο του γραφηματος.
, ισχυει οτι το μεσο του ευθυγραμμου τμηματος που οριζουν ειναι επισης σημειο του γραφηματος. , οι τιμες των σημειων
, οι τιμες των σημειων  , οπου
, οπου  ρητος με τερματιζομενο δυαδικο αναπτυγμα ανηκουν στην ευθεια που οριζεται απο τα
ρητος με τερματιζομενο δυαδικο αναπτυγμα ανηκουν στην ευθεια που οριζεται απο τα  .
. . Ετσι, αφου η
. Ετσι, αφου η  ειναι συνεχης, θα ειναι και γραμμικη.
ειναι συνεχης, θα ειναι και γραμμικη. ειναι λυση. Η
ειναι λυση. Η 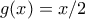 ικανοποιει ολες τις γραμμικες και σταθερες
ικανοποιει ολες τις γραμμικες και σταθερες  .
.s.kap έγραψε:Δεν είμαι σίγουρος για το αν κάνω κατάλληλη επιλογή φακέλλου, αλλά οι μέχρι τώρα προσπάθειες μου δεν έδωσαν αποτέλεσμα, οπότε δεν ξέρω αν τα εργαλεία που χρειάζονται για τη λύση της είναι αυτά που απαιτεί τούτος ο φάκελλος. Την μοιράζομαι μαζί σας :
Να βρεθούν οι συνεχείς συναρτήσεις, για τις οποίες υπάρχει συνάρτηση
, 1-1, ώστε
Φιλικά
 είναι
είναι  οπότε
οπότε 
 και, αφού η
και, αφού η  είναι 1-1,
είναι 1-1, 
 που είναι πάντα λύση αρκεί να επιλέξουμε π.χ.
που είναι πάντα λύση αρκεί να επιλέξουμε π.χ. 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες