 χωρίς προσεγγίσεις ριζών...
χωρίς προσεγγίσεις ριζών...ανισότητα
Συντονιστής: spyros
ανισότητα
Να αποδείξετε ότι
 χωρίς προσεγγίσεις ριζών...
χωρίς προσεγγίσεις ριζών...
 χωρίς προσεγγίσεις ριζών...
χωρίς προσεγγίσεις ριζών...Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: ανισότητα
[Η λύση δεν ολοκληρώνεται]
Η ιδέα είναι να προσεγγίσω το (από πάνω) τόσο καλά ώστε η προσέγγισή του
(από πάνω) τόσο καλά ώστε η προσέγγισή του  να είναι μικρότερη από το
να είναι μικρότερη από το  , ώστε να ισχύει
, ώστε να ισχύει  και άρα
και άρα  .
.
Έστω κύκλος C ακτίνας 1 και κανονικό ν-γωνο περιγεγραμμένο σε αυτόν. Μεταξύ των περιμέτρων του κύκλου και του πολυγώνου
και του πολυγώνου  θα ισχύει
θα ισχύει  <
<  , ενώ
, ενώ  άρα
άρα  ή
ή 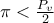 οπότε πρέπει να βρεθεί ένα ικανά "μεγάλο" ν ώστε η περίμετρος του πολυγώνου να είναι
οπότε πρέπει να βρεθεί ένα ικανά "μεγάλο" ν ώστε η περίμετρος του πολυγώνου να είναι  ή
ή  .
.
Έστω Ο το κέντρο του κύκλου, ΑΒ μία πλευρά του ν-γώνου και Μ το σημείο επαφής της με τον κύκλο (ή το μέσο του ΑΒ). Στο ορθογώνιο τρίγωνο ΟΑΜ (η Μ είναι ορθή) έχουμε ,
,  και
και  , ενώ
, ενώ  , άρα
, άρα  , δηλαδή
, δηλαδή  . Έτσι η περίμετρος του πολυγώνου είναι
. Έτσι η περίμετρος του πολυγώνου είναι 
(το σχήμα δίνεται και συνημμένο)
Τελικά, ζητάμε ένα ικανά μεγάλο ν ώστε να ισχύει ή ισοδύναμα
ή ισοδύναμα 
Θα αποδείξω ότι για ν = 48 η παραπάνω απαίτηση ισχύει, δηλαδή ότι .
.
Ξεκινώντας από το ότι και με τους τύπους αποτετραγωνισμού διαδοχικά έχουμε
και με τους τύπους αποτετραγωνισμού διαδοχικά έχουμε
 , άρα
, άρα
 , άρα
, άρα

Το τελευταίο απλοποιείται ως εξής:

Έτσι, μένει να δείξουμε ότι

Στις πράξεις το πράγμα ξεφεύγει σε όγκο αλγεβρικών παραστάσεων και δεν μπόρεσα να βρω κάποιον σύντομο δρόμο μέσω απλοποιήσεων. Το ότι το 48 μας κάνει για την ανίσωση το γνωρίζω με "ζαβολιά" (με τη βοήθεια της GeoGebra, αν θέλετε δείτε το συνημμένο). Μάλιστα, το 48 είναι ο μικρότερος αριθμός και μας κάνει και κάθε μεγαλύτερός του. Οπότε, από εδώ και πέρα είναι "απλώς" θέμα πράξεων!
Η ιδέα είναι να προσεγγίσω το
 (από πάνω) τόσο καλά ώστε η προσέγγισή του
(από πάνω) τόσο καλά ώστε η προσέγγισή του  να είναι μικρότερη από το
να είναι μικρότερη από το  , ώστε να ισχύει
, ώστε να ισχύει  και άρα
και άρα  .
.Έστω κύκλος C ακτίνας 1 και κανονικό ν-γωνο περιγεγραμμένο σε αυτόν. Μεταξύ των περιμέτρων του κύκλου
 και του πολυγώνου
και του πολυγώνου  θα ισχύει
θα ισχύει  <
<  , ενώ
, ενώ  άρα
άρα  ή
ή 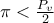 οπότε πρέπει να βρεθεί ένα ικανά "μεγάλο" ν ώστε η περίμετρος του πολυγώνου να είναι
οπότε πρέπει να βρεθεί ένα ικανά "μεγάλο" ν ώστε η περίμετρος του πολυγώνου να είναι  ή
ή  .
.Έστω Ο το κέντρο του κύκλου, ΑΒ μία πλευρά του ν-γώνου και Μ το σημείο επαφής της με τον κύκλο (ή το μέσο του ΑΒ). Στο ορθογώνιο τρίγωνο ΟΑΜ (η Μ είναι ορθή) έχουμε
 ,
,  και
και  , ενώ
, ενώ  , άρα
, άρα  , δηλαδή
, δηλαδή  . Έτσι η περίμετρος του πολυγώνου είναι
. Έτσι η περίμετρος του πολυγώνου είναι 
(το σχήμα δίνεται και συνημμένο)
Τελικά, ζητάμε ένα ικανά μεγάλο ν ώστε να ισχύει
 ή ισοδύναμα
ή ισοδύναμα 
Θα αποδείξω ότι για ν = 48 η παραπάνω απαίτηση ισχύει, δηλαδή ότι
 .
.Ξεκινώντας από το ότι
 και με τους τύπους αποτετραγωνισμού διαδοχικά έχουμε
και με τους τύπους αποτετραγωνισμού διαδοχικά έχουμε , άρα
, άρα , άρα
, άρα
Το τελευταίο απλοποιείται ως εξής:

Έτσι, μένει να δείξουμε ότι

Στις πράξεις το πράγμα ξεφεύγει σε όγκο αλγεβρικών παραστάσεων και δεν μπόρεσα να βρω κάποιον σύντομο δρόμο μέσω απλοποιήσεων. Το ότι το 48 μας κάνει για την ανίσωση το γνωρίζω με "ζαβολιά" (με τη βοήθεια της GeoGebra, αν θέλετε δείτε το συνημμένο). Μάλιστα, το 48 είναι ο μικρότερος αριθμός και μας κάνει και κάθε μεγαλύτερός του. Οπότε, από εδώ και πέρα είναι "απλώς" θέμα πράξεων!
- Συνημμένα
-
- polygon.ggb
- Αρχείο GeoGebra (ggb)
- (6.46 KiB) Μεταφορτώθηκε 35 φορές
-
- Σχήμα
- anisotita_sxima.gif (3.65 KiB) Προβλήθηκε 1084 φορές
Παντελής Πετρίδης
Re: ανισότητα
Παντελή καλώς όρισες στο φόρουμ!
Δεν έχω κάποια λύση και η προσέγγιση που σκέφτηκα είναι εντελώς διαφορετική απότι η δική σου
Συγκεκριμένα σκέφτηκα να διαιρέσω με το 2 οπότε το πρόβλημα μετασχηματίζεται στο εξής

το δεξί μέλος παιδεύτηκα λίγο για να το φτιάξω - σκεφτόμουν ανισότητα hadamard hermitte αλλά μου τα χαλάει στα κοίλα- τέλοσπάντων δεν βλέπω να αποδίδει ο τρόπος που σκέφτηκα.
Θα περιμένουμε λοιπόν για μια λύση
Η άσκηση είναι από μαθλινκσ αναπάντητη απόσο θυμάμαι (έψαξα το λινκ αλλά δεν μπορώ να το εντοπίσω)
Δεν έχω κάποια λύση και η προσέγγιση που σκέφτηκα είναι εντελώς διαφορετική απότι η δική σου
Συγκεκριμένα σκέφτηκα να διαιρέσω με το 2 οπότε το πρόβλημα μετασχηματίζεται στο εξής

το δεξί μέλος παιδεύτηκα λίγο για να το φτιάξω - σκεφτόμουν ανισότητα hadamard hermitte αλλά μου τα χαλάει στα κοίλα- τέλοσπάντων δεν βλέπω να αποδίδει ο τρόπος που σκέφτηκα.
Θα περιμένουμε λοιπόν για μια λύση
Η άσκηση είναι από μαθλινκσ αναπάντητη απόσο θυμάμαι (έψαξα το λινκ αλλά δεν μπορώ να το εντοπίσω)
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
- Ανδρέας Πούλος
- Δημοσιεύσεις: 1494
- Εγγραφή: Κυρ Μαρ 01, 2009 10:47 pm
- Τοποθεσία: ΘΕΣΣΑΛΟΝΙΚΗ
- Επικοινωνία:
Re: ανισότητα
Επιτρέψτέ μου να διαμορφώσω λίγο την εκφώνηση αυτού του πολύ ωραίου προβλήματος.
Να αποδειχθεί με στοιχειώδη Μαθηματικά ότι:
2π > > π.
> π.
Φιλικά,
Ανδρέας Πούλος
Να αποδειχθεί με στοιχειώδη Μαθηματικά ότι:
2π >
 > π.
> π.Φιλικά,
Ανδρέας Πούλος
- Ανδρέας Πούλος
- Δημοσιεύσεις: 1494
- Εγγραφή: Κυρ Μαρ 01, 2009 10:47 pm
- Τοποθεσία: ΘΕΣΣΑΛΟΝΙΚΗ
- Επικοινωνία:
Re: ανισότητα
Διαισθάνομαι ότι το εξαιρετικά χρήσιμο βιβλίο του Τιχομίροφ "Ιστορίες για μέγιστα και ελάχιστα",
εκδόσεις Κάτοπτρο, 1990, μπορεί να μας δώσει καλές ιδέες για τη επίλυση του προβλήματος.
Το ίδιο και το βιβλίο των Andreescu κ.α. "Geometric problems on Maxima and Minima", Birkhauser, 2006.
Φιλικά,
Ανδρέας Πούλος
εκδόσεις Κάτοπτρο, 1990, μπορεί να μας δώσει καλές ιδέες για τη επίλυση του προβλήματος.
Το ίδιο και το βιβλίο των Andreescu κ.α. "Geometric problems on Maxima and Minima", Birkhauser, 2006.
Φιλικά,
Ανδρέας Πούλος
-
kwstas12345
- Δημοσιεύσεις: 1055
- Εγγραφή: Δευ Ιαν 11, 2010 2:12 pm
Re: ανισότητα
Mια απάντηση στο νέο φράγμα του κ.Ανδρέα:
Eίναι:

Φιλικά,
Κώστας
Eίναι:

Φιλικά,
Κώστας
τελευταία επεξεργασία από kwstas12345 σε Δευ Αύγ 30, 2010 2:41 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
kwstas12345
- Δημοσιεύσεις: 1055
- Εγγραφή: Δευ Ιαν 11, 2010 2:12 pm
Re: ανισότητα
Nομίζω πως το άνω φράγμα μπορεί να βελτιωθεί περαιτέρω.Άς δειχτεί λοιπόν:  .
.
Φιλικά,
Κώστας
 .
.Φιλικά,
Κώστας
- Ανδρέας Πούλος
- Δημοσιεύσεις: 1494
- Εγγραφή: Κυρ Μαρ 01, 2009 10:47 pm
- Τοποθεσία: ΘΕΣΣΑΛΟΝΙΚΗ
- Επικοινωνία:
Re: ανισότητα
Αγαπητέ Κώστα, δεν παίζω. Χρησιμοποιείς "παράνομα" μέσα. Είπαμε εντελώς στοιχειώδη Μαθηματικά.
΄Οχι συνάρτηση Riemann κλπ. Πάντως, μου άρεσε η απόδειξή σου.
Όμως, υπάρχουν και τα αρχιαοελληνικά κόλπα.
Για παράδειγμα, μία απλή απόδειξη για την σχέση είναι η ακόλουθη.
είναι η ακόλουθη.
Κατασκευάζουμε κύκλο ακτίνας 1 και εγγράφουμε σε αυτόν τετράγωνο.
Αυτό έχει πλευρά μήκους .
.
Ο κύκλος έχει περίμετρο 2π. Άρα .
.
Όμως, .
.
Συνεπώς, .
.
Το ζόρικο θέμα είναι η άλλη (η αρχική ανισότητα). Προκαλούμε τους φίλους για εντελώς στοιχειώδη απόδειξη.
Φιλικά,
Ανδρέας Πούλος
΄Οχι συνάρτηση Riemann κλπ. Πάντως, μου άρεσε η απόδειξή σου.
Όμως, υπάρχουν και τα αρχιαοελληνικά κόλπα.
Για παράδειγμα, μία απλή απόδειξη για την σχέση
 είναι η ακόλουθη.
είναι η ακόλουθη.Κατασκευάζουμε κύκλο ακτίνας 1 και εγγράφουμε σε αυτόν τετράγωνο.
Αυτό έχει πλευρά μήκους
 .
.Ο κύκλος έχει περίμετρο 2π. Άρα
 .
.Όμως,
 .
. Συνεπώς,
 .
.Το ζόρικο θέμα είναι η άλλη (η αρχική ανισότητα). Προκαλούμε τους φίλους για εντελώς στοιχειώδη απόδειξη.
Φιλικά,
Ανδρέας Πούλος
- Ανδρέας Πούλος
- Δημοσιεύσεις: 1494
- Εγγραφή: Κυρ Μαρ 01, 2009 10:47 pm
- Τοποθεσία: ΘΕΣΣΑΛΟΝΙΚΗ
- Επικοινωνία:
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3342
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: ανισότητα
Από το ότι το εμβαδόν του κανονικού δωδεκαγώνου εγγεγραμμένου σε κύκλο ακτίνας 1 ισούται προς 3Ανδρέας Πούλος έγραψε:από που προκύπτει ότι 2π > 6;
Όσον αφορά την αρχική ανισότητα, μπορούμε απλά να εκμεταλλευθούμε την αναπόφευκτα στοιχειώδη ανισότητα του Αρχιμήδη,
 (χρήση κανονικού 96-γώνου), σε συνδυασμό με την
(χρήση κανονικού 96-γώνου), σε συνδυασμό με την  (που είναι ισοδύναμη, ύστερα από δυο υψώσεις στο τετράγωνο και απαλοιφή παρονομαστών, προς την
(που είναι ισοδύναμη, ύστερα από δυο υψώσεις στο τετράγωνο και απαλοιφή παρονομαστών, προς την  )
) Γιώργος Μπαλόγλου
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3342
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: ανισότητα
Και με κανονικό 48-γωνο γίνεται, για όποιον μπορεί να αποδείξει με το χέρι την ![48[\frac{-t^{2}+2\sqrt{2t^{2}-t}}{2t-1}]<\sqrt{2}+\sqrt{3} 48[\frac{-t^{2}+2\sqrt{2t^{2}-t}}{2t-1}]<\sqrt{2}+\sqrt{3}](/forum/ext/geomar/texintegr/latexrender/pictures/c838ef2c6ca3f8aac4171e7c1e040466.png) , όπου
, όπου 

[Το εμβαδόν του μοναδιαίου κύκλου, , είναι μικρότερο από το εμβαδόν του περιγεγραμμένου κανονικού 48-γώνου,
, είναι μικρότερο από το εμβαδόν του περιγεγραμμένου κανονικού 48-γώνου, ![48[tan\frac{\pi}{48}] 48[tan\frac{\pi}{48}]](/forum/ext/geomar/texintegr/latexrender/pictures/a8c567d187c04e90d5308831ced408a5.png) ^ για την
^ για την  χρησιμοποιούμε 3 φορές τον τύπο
χρησιμοποιούμε 3 φορές τον τύπο 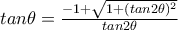 αρχίζοντας βέβαια από την
αρχίζοντας βέβαια από την  .]
.]
Γιώργος Μπαλόγλου
ΥΓ Για την ανισότητα του Αρχιμήδη, , βρήκα το άρθρο του Burton Rosenberg "Archimedes and Pi", δείτε εδώ
, βρήκα το άρθρο του Burton Rosenberg "Archimedes and Pi", δείτε εδώ
![48[\frac{-t^{2}+2\sqrt{2t^{2}-t}}{2t-1}]<\sqrt{2}+\sqrt{3} 48[\frac{-t^{2}+2\sqrt{2t^{2}-t}}{2t-1}]<\sqrt{2}+\sqrt{3}](/forum/ext/geomar/texintegr/latexrender/pictures/c838ef2c6ca3f8aac4171e7c1e040466.png) , όπου
, όπου 
[Το εμβαδόν του μοναδιαίου κύκλου,
 , είναι μικρότερο από το εμβαδόν του περιγεγραμμένου κανονικού 48-γώνου,
, είναι μικρότερο από το εμβαδόν του περιγεγραμμένου κανονικού 48-γώνου, ![48[tan\frac{\pi}{48}] 48[tan\frac{\pi}{48}]](/forum/ext/geomar/texintegr/latexrender/pictures/a8c567d187c04e90d5308831ced408a5.png) ^ για την
^ για την  χρησιμοποιούμε 3 φορές τον τύπο
χρησιμοποιούμε 3 φορές τον τύπο 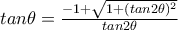 αρχίζοντας βέβαια από την
αρχίζοντας βέβαια από την  .]
.]Γιώργος Μπαλόγλου
ΥΓ Για την ανισότητα του Αρχιμήδη,
 , βρήκα το άρθρο του Burton Rosenberg "Archimedes and Pi", δείτε εδώ
, βρήκα το άρθρο του Burton Rosenberg "Archimedes and Pi", δείτε εδώΓιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες

