Κάθε επιτυχία στους μαθητές της Γ΄ Λυκείου που δίνουν έναν πολύ δύσκολο αγώνα.
Παρακάτω, ένα δικό μου διαγώνισμα στο 1ο κεφάλαιο της Ανάλυσης.
Για όσους το θέλουν σε .doc μπορούν να το κατεβάσουν από εδώ
ΔΙΑΓΩΝΙΣΜΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ΄ ΛΥΚΕΙΟΥ
ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΜΑΘΗΜΑΤΙΚΑ
ΟΡΙΟ ΚΑΙ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
ΘΕΜΑ 1ο
A. Πότε μια συνάρτηση λέμε ότι είναι συνεχής στο [α,β]; ......................Μονάδες 9
B. Να διατυπώσετε και να αποδείξετε το θεώρημα ενδιάμεσων τιμών ......Μονάδες 10.
Γ. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας την ένδειξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση.
α. Αν η συνάρτηση f είναι ορισμένη στο
 και
και  τότε, σε κάθε περίπτωση,
τότε, σε κάθε περίπτωση,  =
=  .....Μονάδες 1
.....Μονάδες 1 β. Αν για δύο συναρτήσεις f , g ισχύουν :
 και
και  τότε το όριο
τότε το όριο  είναι καλά ορισμένο και είναι ίσο με το 0 .....Μονάδες 1
είναι καλά ορισμένο και είναι ίσο με το 0 .....Μονάδες 1 γ. Αν η συνάρτηση f είναι ορισμένη στο διάστημα Δ και ισχύει:
 για κάθε x ε Δ τότε οπωσδήποτε η f θα διατηρεί σταθερό πρόσημο στο Δ.......Μονάδες 1
για κάθε x ε Δ τότε οπωσδήποτε η f θα διατηρεί σταθερό πρόσημο στο Δ.......Μονάδες 1 δ. Αν η συνάρτηση f είναι ορισμένη στο IR και συνεχής στο διάστημα [α , β] τότε αναγκαστικά θα είναι συνεχής στα α, β .....Μονάδες 1
ε. Αν η συνάρτηση f είναι συνεχής στο διάστημα Δ τότε αναγκαστικά θα παρουσιάζει μέγιστη και ελάχιστη τιμή στο Δ .......Μονάδες 1
στ. Το σύνολο τιμών μιας συνεχούς συνάρτησης f στο Δ=[α,β] είναι πάντα το [f(α),f(β)] ......Μονάδες 1
ΘΕΜΑ 2ο
Δίνεται η συνεχής και γνησίως αύξουσα συνάρτηση
 για την οποία ισχύουν:
για την οποία ισχύουν: 
και

α. Να δείξετε ότι υπάρχει μοναδικό
 τέτοιο ώστε:
τέτοιο ώστε:  ......Μονάδες 8
......Μονάδες 8 β. Να δείξετε ότι
 ......Μονάδες 9
......Μονάδες 9 γ. Να βρείτε το σύνολο τιμών της
 .....Μονάδες 8
.....Μονάδες 8 ΘΕΜΑ 3ο
Δίνεται η συνάρτηση
 ,
,  και
και  .
.Α. Για τις διάφορες τιμές του
 να βρείτε το
να βρείτε το ....Μονάδες 8
....Μονάδες 8Β. Έστω ότι

α. Να μελετήσετε την συνάρτηση
 ως προς τη μονοτονία......Μονάδες 5
ως προς τη μονοτονία......Μονάδες 5β. Να βρείτε το σύνολο τιμών της
 .......Μονάδες 6
.......Μονάδες 6γ. Να ορίσετε την αντίστροφή της .......Μονάδες 6
ΘΕΜΑ 4ο
Δίνεται η συνεχής συνάρτηση
 ,για την οποία ισχύει
,για την οποία ισχύει 
Α.
α. Να βρείτε το
 .....Μονάδες 3
.....Μονάδες 3β. Να βρείτε το όριο:
 .....Μονάδες 5
.....Μονάδες 5Β. Αν επιπλέον για την f ισχύει:

α. Να δείξετε ότι:
 ......Μονάδες7
......Μονάδες7 β. Να υπολογίσετε τα όρια
 και
και  ......Mονάδες 5
......Mονάδες 5 γ. Να χρησιμοποιήσετε δεδομένο ότι η συνάρτηση είναι γνησίως φθίνουσα στο
![\displaystyle{\left( { - \infty ,0} \right]} \displaystyle{\left( { - \infty ,0} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ac38e9c7e5aa7ab14f64b51460ee5b0d.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  για να δείξετε ότι η εξίσωση:
για να δείξετε ότι η εξίσωση:  έχει δύο ακριβώς ρίζες για κάθε τιμή του
έχει δύο ακριβώς ρίζες για κάθε τιμή του με
με  .....Μονάδες 5
.....Μονάδες 5
 και
και 

 έτσι ώστε
έτσι ώστε
![x\in [0,3] x\in [0,3]](/forum/ext/geomar/texintegr/latexrender/pictures/304c30b2e809aa1ba319fe4bb74ca012.png) και ξέρουμε πως
και ξέρουμε πως


![\lim_{x\rightarrow 0}\left(ln(x+1)-lnx\right)=\lim_{x\rightarrow 0}\frac{ln(x+1)}{lnx}=\lim_{x\rightarrow 0}\left[-lnx\cdot ln(x+1) \right]=\lim_{x\rightarrow 0}-lnx \cdot \lim_{x\rightarrow 0} ln(x+1)=+ \infty \lim_{x\rightarrow 0}\left(ln(x+1)-lnx\right)=\lim_{x\rightarrow 0}\frac{ln(x+1)}{lnx}=\lim_{x\rightarrow 0}\left[-lnx\cdot ln(x+1) \right]=\lim_{x\rightarrow 0}-lnx \cdot \lim_{x\rightarrow 0} ln(x+1)=+ \infty](/forum/ext/geomar/texintegr/latexrender/pictures/59e6e36e9cdca8a6c17156492c807112.png)
![lim_{x\rightarrow 0}\left[ ln(ax^2+x+1)-ln((1+a)+a) \right]=ln1-lna=-lna lim_{x\rightarrow 0}\left[ ln(ax^2+x+1)-ln((1+a)+a) \right]=ln1-lna=-lna](/forum/ext/geomar/texintegr/latexrender/pictures/fce19d745bdf72872f43dd920a93b6b5.png)
 διότι
διότι  και
και  και αυτό γιατί η f γνησίως αύξουσα άρα έχει το πολύ μια λύση. Αν λοιπόν ήταν f(3)=0 ή f(0)=0 και επειδή f(0)= -f(3) (για x=0 στην αρχική σχέση) τότε θα ίσχυε f(3)=f(0)=0. Επομένως η f θα είχε δύο λύσεις άτοπο. Άρα
και αυτό γιατί η f γνησίως αύξουσα άρα έχει το πολύ μια λύση. Αν λοιπόν ήταν f(3)=0 ή f(0)=0 και επειδή f(0)= -f(3) (για x=0 στην αρχική σχέση) τότε θα ίσχυε f(3)=f(0)=0. Επομένως η f θα είχε δύο λύσεις άτοπο. Άρα  επομένως η συνεχής συνάρτηση f έχει τουλάχιστον μια λύση
επομένως η συνεχής συνάρτηση f έχει τουλάχιστον μια λύση  και επειδή η f γνησίως αύξουσα η λύση
και επειδή η f γνησίως αύξουσα η λύση  είναι μοναδική.
είναι μοναδική. και όχι το
και όχι το  .
.
 θα γίνει
θα γίνει 
 θα διατηρεί πρόσημο λόγω συνέχειας άρα θα είναι
θα διατηρεί πρόσημο λόγω συνέχειας άρα θα είναι 
 είναι δεκτή μιας και
είναι δεκτή μιας και 
 . Όμως, δεν μπορεί
. Όμως, δεν μπορεί  , διαφορετικά και από τη σχέση
, διαφορετικά και από τη σχέση  θα έπρεπε:
θα έπρεπε:  .
.  .
. . Άρα για
. Άρα για  είναι
είναι  . Μάλιστα το
. Μάλιστα το  είναι ο μοναδικός πραγματικός αριθμός για τον οποίο
είναι ο μοναδικός πραγματικός αριθμός για τον οποίο  εξίσωση δευτέρου βαθμού με άγνωστο το f(x) καταλήγουμε στις
εξίσωση δευτέρου βαθμού με άγνωστο το f(x) καταλήγουμε στις  από τις οποίες η πρώτη είναι δεκτη καθώς επαληθεύει την f(0)=2
από τις οποίες η πρώτη είναι δεκτη καθώς επαληθεύει την f(0)=2 εξίσωση δευτέρου βαθμού με άγνωστο το
εξίσωση δευτέρου βαθμού με άγνωστο το  καταλήγουμε στις
καταλήγουμε στις 



 (αλλιώς θα ήταν
(αλλιώς θα ήταν 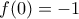 ) , προκύπτει
) , προκύπτει  ο.ε.δ.
ο.ε.δ. για κάποιο
για κάποιο  ,τότε
,τότε  άτοπο,
άτοπο,  συνεχής και
συνεχής και  τότε :
τότε : κ.λ.π.
κ.λ.π. γνωρίζουμε, από το Α.α., ότι ισχύει:
γνωρίζουμε, από το Α.α., ότι ισχύει:  .
. 
 .
.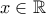 . Σύμφωνα με την
. Σύμφωνα με την  , ο πραγματικός αριθμός
, ο πραγματικός αριθμός  θα είναι ρίζα της εξίσωσης:
θα είναι ρίζα της εξίσωσης: .
. . Οπότε η εξίσωση
. Οπότε η εξίσωση  έχει δύο άνισες ρίζες:
έχει δύο άνισες ρίζες: 
 .
. μπορούμε να δημιουργήσουμε άπειρες συναρτήσεις που να έχουν
μπορούμε να δημιουργήσουμε άπειρες συναρτήσεις που να έχουν  να επιλέγουμε ότι θέλουμε, μεταξύ των
να επιλέγουμε ότι θέλουμε, μεταξύ των  και
και  , σαν
, σαν  για κάθε
για κάθε  και αυτό γιατί:
και αυτό γιατί: και εφόσον η συνάρτησή μας είναι συνεχής, από το θεώρημα του Bolzano, θα πρέπει να διατηρεί σταθερό πρόσημο στο
και εφόσον η συνάρτησή μας είναι συνεχής, από το θεώρημα του Bolzano, θα πρέπει να διατηρεί σταθερό πρόσημο στο  .
.  ή
ή  .
.  , άρα θα πρέπει:
, άρα θα πρέπει:  .
.