Θερμή παράκληση να χρησιμοποιούνται Ελληνικά και όποιος φίλος χρησιμοποιεί Geogebra ας επισυνάπτει και το αρχείο ggb (για δική μου διευκόλυνση).
Άσκηση 001 Δίνεται τετράγωνο
 με κέντρο
με κέντρο  . Αν για τυχαία σημεία
. Αν για τυχαία σημεία  επί των πλευρών
επί των πλευρών  αντίστοιχα ισχύει
αντίστοιχα ισχύει  , δείξτε ότι:
, δείξτε ότι:1)
 .
.2)
 .
.
 τα μέσα των πλευρών
τα μέσα των πλευρών  αντίστοιχα.
αντίστοιχα.  είναι τετράγωνο με μήκος πλευράς το μισό
είναι τετράγωνο με μήκος πλευράς το μισό  .
.  . Τα ορθογώνια τρίγωνα
. Τα ορθογώνια τρίγωνα  έχουν τις κάθετες πλευρές τους
έχουν τις κάθετες πλευρές τους  ίσες και τις
ίσες και τις  ίσες άρα είναι ίσα και έτσι θα είναι και ισοδύναμα
ίσες άρα είναι ίσα και έτσι θα είναι και ισοδύναμα  δηλαδή
δηλαδή 
 .
. κατασκευάζω εξωτερικά το ισόπλευρο
κατασκευάζω εξωτερικά το ισόπλευρο  . Αν
. Αν  , δείξτε ότι
, δείξτε ότι  .
. κι επειδή
κι επειδή  , όπου
, όπου  η πλευρά του τετραγώνου ,θα είναι
η πλευρά του τετραγώνου ,θα είναι  κι έτσι τα τρίγωνα
κι έτσι τα τρίγωνα  είναι ίσα οπότε
είναι ίσα οπότε  κι ακόμη
κι ακόμη  και
και  .Άρα
.Άρα 
 η προβολή της
η προβολή της  στην
στην  .Προφανώς
.Προφανώς  . Τώρα με γενικευμένο Πυθαγόρειο θεώρημα στο αμβλυγώνιο τρίγωνο
. Τώρα με γενικευμένο Πυθαγόρειο θεώρημα στο αμβλυγώνιο τρίγωνο  παίρνουμε
παίρνουμε 
 κατασκευάζω εσωτερικά το ισόπλευρο
κατασκευάζω εσωτερικά το ισόπλευρο  . Αν
. Αν  τετράγωνο στο ημιεπίπεδο που ορίζεται απ’ την
τετράγωνο στο ημιεπίπεδο που ορίζεται απ’ την  και στο οποίο δεν ανήκει το
και στο οποίο δεν ανήκει το  , να δείξετε ότι
, να δείξετε ότι  .
.

 είναι ισόπλευρο αφού
είναι ισόπλευρο αφού  και
και 

 , τέτοιο ώστε
, τέτοιο ώστε  και
και  . Να δείξετε ότι
. Να δείξετε ότι  .
. και το τρίγωνο
και το τρίγωνο  έχει
έχει  .
. προφανώς
προφανώς  και το ζητούμενο αποδείχτηκε .
και το ζητούμενο αποδείχτηκε . και
και όπου
όπου  το μέσο του
το μέσο του 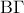 .
. είναι ισοσκελή με κορυφές
είναι ισοσκελή με κορυφές  αντίστοιχα και επειδή
αντίστοιχα και επειδή  , θα είναι όμοια με
, θα είναι όμοια με  .
. το μέσο της
το μέσο της  , να δείξετε ότι
, να δείξετε ότι  .
. είναι ως γνωστό όμοια .
είναι ως γνωστό όμοια . , αν
, αν  και
και  , θα είναι:
, θα είναι: . Ας πούμε
. Ας πούμε  , από την ομοιότητα των τριγώνων
, από την ομοιότητα των τριγώνων  θα έχουμε :
θα έχουμε : . Από το Πυθαγόρειο θεώρημα στο τρίγωνο
. Από το Πυθαγόρειο θεώρημα στο τρίγωνο  , θα προκύψει :
, θα προκύψει :  .
. .
.  ισχύει :
ισχύει :  η
η  γίνεται :
γίνεται : .
. , να δείξετε ότι
, να δείξετε ότι  .
.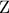 το σημείο τομής των
το σημείο τομής των  . Τα ορθογώνια τρίγωνα
. Τα ορθογώνια τρίγωνα  έχουν τις κάθετες πλευρές του
έχουν τις κάθετες πλευρές του  ίσες και τις
ίσες και τις  γιατί έχουν κάθετες πλευρές , οπότε θα είναι
γιατί έχουν κάθετες πλευρές , οπότε θα είναι  . έτσι όμως θα ισχύει και
. έτσι όμως θα ισχύει και  .
. 
 είναι όμοια επειδή είναι ορθογώνια κι επειδή
είναι όμοια επειδή είναι ορθογώνια κι επειδή  .
. βρίσκουμε με Π.Θ. πως ισούται με
βρίσκουμε με Π.Θ. πως ισούται με  .
. .
. .
. όσο δηλαδή το εμβαδόν του τριγώνου μας.
όσο δηλαδή το εμβαδόν του τριγώνου μας.
 .Το
.Το  είναι εγγράψιμο οπότε
είναι εγγράψιμο οπότε  .Αλλά τα τρίγωνα
.Αλλά τα τρίγωνα  είναι ίσα αφού
είναι ίσα αφού  (οξείες με κάθετες πλευρές) κι έτσι
(οξείες με κάθετες πλευρές) κι έτσι  .Άρα
.Άρα 
 . Αν
. Αν  , να δείξετε ότι:
, να δείξετε ότι: .
. .
. έχουμε ότι
έχουμε ότι 

 .Οπότε
.Οπότε 
 έχουμε
έχουμε



 .Οπότε
.Οπότε 
 έχουμε
έχουμε


 .
. είναι ίσα.
είναι ίσα. και
και 
 είναι εγγράψιμο άρα
είναι εγγράψιμο άρα 