Δεν έχω το βιβλίο των Kaczor, Nowak για να συγκρίνω αλλά το πιστεύω ότι είναι δύσκολη η άσκηση.
Από κάτω δίνω λύση με την επιπλέον υπόθεση

γιατί από μόνη της είναι ενδιαφέρουσα και (μάλλον) απλούστερη από την γενική περίπτωση (που δεν είδα).
AlexandrosG έγραψε:
Άσκηση 3
Έστω

ακολουθία πραγματικών αριθμών τέτοια ώστε η σειρά

να συγκλίνει. Να δειχθεί ότι

Έστω ότι

. Άρα υπάρχει

και άπειρο σύνολο δεικτών

με

Ορίζουμε επαγωγικά ακολουθία

στοιχείων του

με

ως εξής.
Για το επαγωγικό βήμα, αφού έχουμε επιλέξει τον

, επιλέγουμε

τόσο μεγάλο ώστε να ισχύει

Είναι τότε

, όπως θέλαμε.
Έχουμε τώρα (εδώ μπαίνει η υπόθεση

)

που σημαίνει ότι η

αποκλίνει αφού δεν είναι Cauchy.
Από το άτοπο έπεται το ζητούμενο.
Φιλικά,
Μιχάλης
 μετρικός χώρος.Αποδείξτε ότι κάθε κλειστό υποσύνολο του
μετρικός χώρος.Αποδείξτε ότι κάθε κλειστό υποσύνολο του  γράφεται ως αριθμήσιμη τομή ανοιχτών συνόλων και κάθε ανοιχτό υποσύνολο του
γράφεται ως αριθμήσιμη τομή ανοιχτών συνόλων και κάθε ανοιχτό υποσύνολο του  γράφεται ως αριθμήσιμη ένωση κλειστών συνόλων.
γράφεται ως αριθμήσιμη ένωση κλειστών συνόλων. υπάρχει άπειρο υποσύνολό
υπάρχει άπειρο υποσύνολό  του
του  ώστε κάθε
ώστε κάθε  να είναι ανοιχτό ως προς τη σχετική μετρική στο
να είναι ανοιχτό ως προς τη σχετική μετρική στο  ;
;
 το οποίο είναι κλειστό. Για κάθε
το οποίο είναι κλειστό. Για κάθε  ορίζουμε
ορίζουμε  .
.  είναι ανοιχτό ως ένωση ανοιχτών σφαιρών.
είναι ανοιχτό ως ένωση ανοιχτών σφαιρών. , άρα αρκεί να δείξω ότι
, άρα αρκεί να δείξω ότι  .
. . Θα δείξω ότι
. Θα δείξω ότι  .
. είναι ανοιχτό άρα υπάρχει
είναι ανοιχτό άρα υπάρχει  . Δηλαδή για όλα τα
. Δηλαδή για όλα τα  έχουμε ότι
έχουμε ότι  .
.  .
.
 .
. έδειξες ότι υπάρχει
έδειξες ότι υπάρχει  εξαρτάται από το
εξαρτάται από το  ακολουθία πραγματικών αριθμών τέτοια ώστε η σειρά
ακολουθία πραγματικών αριθμών τέτοια ώστε η σειρά  να συγκλίνει. Να δειχθεί ότι
να συγκλίνει. Να δειχθεί ότι 
 και
και  έτσι ώστε
έτσι ώστε  ενώ
ενώ  ?
? -σύνολο και κάθε ανοικτό υποσύνολο ενός μετρικού χώρου είναι
-σύνολο και κάθε ανοικτό υποσύνολο ενός μετρικού χώρου είναι  -σύνολο.
-σύνολο. κλειστό υποσύνολο του
κλειστό υποσύνολο του  η συνάρτηση απόστασης από το σύνολο
η συνάρτηση απόστασης από το σύνολο  θεωρούμε το σύνολο
θεωρούμε το σύνολο  .
.  είναι (ομοιόμορφα) συνεχής, το σύνολο
είναι (ομοιόμορφα) συνεχής, το σύνολο  είναι ανοικτό στο
είναι ανοικτό στο  ,
,  είναι ανοικτό υποσύνολο του
είναι ανοικτό υποσύνολο του  για κάθε
για κάθε  .
. τότε
τότε  για κάθε
για κάθε  για κάθε
για κάθε  οπότε
οπότε  ,αφού το
,αφού το  .
. είναι ανοικτό υποσύνολο του
είναι ανοικτό υποσύνολο του  είναι κλειστό υποσύνολο του
είναι κλειστό υποσύνολο του  οπότε
οπότε  , όπου
, όπου  κλειστό υποσύνολο του
κλειστό υποσύνολο του  με
με  και
και  η ευκλείδεια μετρική.
η ευκλείδεια μετρική. και
και 
 ενώ
ενώ 
 όπου οι αριθμοί
όπου οι αριθμοί 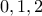 λαμβάνονται (στην σωστή τους θέση) πάνω στον άξονα των πραγματικών.
λαμβάνονται (στην σωστή τους θέση) πάνω στον άξονα των πραγματικών.  έχουμε
έχουμε 
 δεν πήγαινε στο
δεν πήγαινε στο  θα υπήρχε
θα υπήρχε 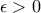 και
και  γνησίως αύξουσα ακολουθία φυσικών ώστε
γνησίως αύξουσα ακολουθία φυσικών ώστε  .Τότε όμως η δοθείσα σειρά θα απόκλινε.
.Τότε όμως η δοθείσα σειρά θα απόκλινε. .
. .
.  συγκλίνει στο
συγκλίνει στο  όποτε
όποτε  και
και  αλλά
αλλά 
 γιατί από μόνη της είναι ενδιαφέρουσα και (μάλλον) απλούστερη από την γενική περίπτωση (που δεν είδα).
γιατί από μόνη της είναι ενδιαφέρουσα και (μάλλον) απλούστερη από την γενική περίπτωση (που δεν είδα). . Άρα υπάρχει
. Άρα υπάρχει  και άπειρο σύνολο δεικτών
και άπειρο σύνολο δεικτών  με
με 
 στοιχείων του
στοιχείων του  με
με  ως εξής.
ως εξής. , επιλέγουμε
, επιλέγουμε  τόσο μεγάλο ώστε να ισχύει
τόσο μεγάλο ώστε να ισχύει 
 , όπως θέλαμε.
, όπως θέλαμε. )
) 
 αποκλίνει αφού δεν είναι Cauchy.
αποκλίνει αφού δεν είναι Cauchy.  μη κενό και κλειστό υποσύνολο του
μη κενό και κλειστό υποσύνολο του  συνεχής συνάρτηση.Δείξτε ότι υπάρχει συνεχής
συνεχής συνάρτηση.Δείξτε ότι υπάρχει συνεχής  έτσι ώστε
έτσι ώστε  για κάθε
για κάθε  .
. είναι ανοικτό αν και μόνο αν το σύνολο
είναι ανοικτό αν και μόνο αν το σύνολο  είναι κλειστό, συμπεραίνουμε ότι η ένωση οσωνδήποτε κλειστών συνόλων είναι κλειστό σύνολο. Τα μονοσύνολα είναι κλειστά και συνεπώς οποιοδήποτε σύνολο είναι κλειστό. Ξανά από την ισοδυναμία οποιοδήποτε σύνολο είναι και ανοικτό. Να σημειώσω εδώ ότι τότε ο χώρος λέγεται διακριτός και μια μετρική που επάγει αυτήν την τοπολογία είναι η
είναι κλειστό, συμπεραίνουμε ότι η ένωση οσωνδήποτε κλειστών συνόλων είναι κλειστό σύνολο. Τα μονοσύνολα είναι κλειστά και συνεπώς οποιοδήποτε σύνολο είναι κλειστό. Ξανά από την ισοδυναμία οποιοδήποτε σύνολο είναι και ανοικτό. Να σημειώσω εδώ ότι τότε ο χώρος λέγεται διακριτός και μια μετρική που επάγει αυτήν την τοπολογία είναι η  για
για  ενώ
ενώ  για
για  .
.![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) είναι ομοιομορφικό με το
είναι ομοιομορφικό με το  μέσω της
μέσω της  αλλά το μεν πρώτο είναι ολικά φραγμένο (άμεσο) αλλά όχι το δεύτερο (αφού δεν είναι καν φραγμένο).
αλλά το μεν πρώτο είναι ολικά φραγμένο (άμεσο) αλλά όχι το δεύτερο (αφού δεν είναι καν φραγμένο).  με την συνήθη μετρική και, κατόπιν, με την μετρική
με την συνήθη μετρική και, κατόπιν, με την μετρική .
.  μέσω της
μέσω της  αλλά, φυσικά, το
αλλά, φυσικά, το