52 φύλλα της τράπουλας
Συντονιστής: Γιώργος Ρίζος
52 φύλλα της τράπουλας
Βρίσκεσαι σε ένα δωμάτιο όπου έχεις άπειρες μπερδεμένες τράπουλες, γυρισμένες ανάποδα (δε μπορείς να προβλέψεις τι θα τραβήξεις και κάθε φορά που τραβάς ένα φύλλο έχεις τις ίδιες πιθανότητες να σου ξανατύχει). Πόσα φύλλα κατά μέσο όρο χρειάζεται να τραβήξεις για να σχηματίσεις και τα 52 φύλλα της τράπουλας;
Re: 52 φύλλα της τράπουλας
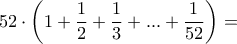
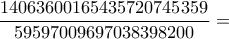
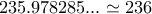
Αν νομίζεις-θεωρείς σωστό εσύ ή οποιοσδήποτε άλλος να γράψω και μερικά λογάκια για το πως φτάνουμε σε αυτό το αποτέλεσμα, ευχαρίστως να το κάνω.
Υ.Γ Η στρογγυλοποίηση
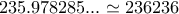 μάλλον δεν χρειάζεται αφού μιλάμε για Μ.Ο
μάλλον δεν χρειάζεται αφού μιλάμε για Μ.ΟRe: 52 φύλλα της τράπουλας
Λίγα λογάκια δε θα ηταν άσχημα!! 
Απ' ότι έχω καταλάβει όμως τα διασκεδαστικά μαθηματικα είναι τα αγαπημένα σου. Όποτε ανεβάζω εσύ μου το λύνεις!!
Απ' ότι έχω καταλάβει όμως τα διασκεδαστικά μαθηματικα είναι τα αγαπημένα σου. Όποτε ανεβάζω εσύ μου το λύνεις!!
Re: 52 φύλλα της τράπουλας
Μετά από την τόσο κομψή διατύπωση , δεν μπορώ παρά να γράψω όσο πιο αναλυτικά μπορώ!Silver έγραψε:Λίγα λογάκια δε θα ήταν άσχημα!!
Kαταρχάς αφού οι τράπουλες είναι άπειρες,- άρα και τα
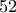 είδη φύλλων είναι άπειρα - όταν τραβήξουμε
είδη φύλλων είναι άπειρα - όταν τραβήξουμε  (
( πεπερασμένος αριθμός) πάλι άπειρα μένουν ή ισοδύναμα σαν να έχουμε μία τράπουλα και κάθε φορά που τραβάμε ένα φύλλο το επανατοποθετούμε - ας πούμε ότι την επανατοποθέτηση την κάνει κάποιος άλλος, - χωρίς να γνωρίζουμε την θέση του.
πεπερασμένος αριθμός) πάλι άπειρα μένουν ή ισοδύναμα σαν να έχουμε μία τράπουλα και κάθε φορά που τραβάμε ένα φύλλο το επανατοποθετούμε - ας πούμε ότι την επανατοποθέτηση την κάνει κάποιος άλλος, - χωρίς να γνωρίζουμε την θέση του.Τραβώντας το πρώτο φύλλο ότι και να είναι μας κάνει, η πιθανότητα να συμβεί αυτό είναι
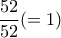 .
. Tραβώντας για δεύτερο φύλλο σxηματισμού της τράπουλας όποιο από τα υπόλοιπα
 είδη τραβήξουμε μας κάνει, η πιθανότητα να συμβεί είναι
είδη τραβήξουμε μας κάνει, η πιθανότητα να συμβεί είναι 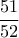 , oπότε ο μέσος όρος φύλλων που πρέπει να τραβήξουμε για την εύρεση διαφορετικού από το πρώτο φύλλο είναι
, oπότε ο μέσος όρος φύλλων που πρέπει να τραβήξουμε για την εύρεση διαφορετικού από το πρώτο φύλλο είναι 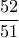 κ.ο.κ για την εύρεση τρίτου φύλλου διαφορετικού από τα δύο πρώτα, όποιο από τα υπόλοιπα
κ.ο.κ για την εύρεση τρίτου φύλλου διαφορετικού από τα δύο πρώτα, όποιο από τα υπόλοιπα  διαφορετικά φύλλα μας κάνει, άρα πιθανότητα
διαφορετικά φύλλα μας κάνει, άρα πιθανότητα 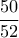 και ο μέσος απαιτούμενος αριθμός φύλλων
και ο μέσος απαιτούμενος αριθμός φύλλων 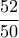 ,...., και για το
,...., και για το 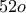 της υπό σχηματισμόν τράπουλας η πιθανότητα είναι
της υπό σχηματισμόν τράπουλας η πιθανότητα είναι 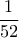 , οπότε ο απαιτούμενος μέσος αριθμός τυχαίων φύλλων που πρέπει να τραβήξουμε είναι
, οπότε ο απαιτούμενος μέσος αριθμός τυχαίων φύλλων που πρέπει να τραβήξουμε είναι 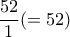
Άρα αθροιστικά ο μ. όρος φύλλων που χρειάζεται να τραβήξουμε για τον σχηματισμό μιας πλήρους τράπουλας είναι το άθροισμα των επί μέρους μ. όρων για καθένα από αυτά ήτοι:
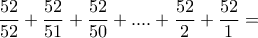
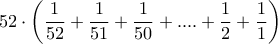 = το παραπάνω αποτέλεσμα.
= το παραπάνω αποτέλεσμα.Ναι, σωστή ... η διάγνωση! Σε επίπεδο μαθηματικών τα διασκεδαστικά μαθηματικά, οι μαθηματικοί γρίφοι, η συνδυαστική και η συνδυαστική γεωμετρία έχουν - τα τριάμισυ περίπου χρόνια που ασχολούμαι - την πρώτη θέση μακράν.Silver έγραψε: Απ' ότι έχω καταλάβει όμως τα διασκεδαστικά μαθηματικά είναι τα αγαπημένα σου. Όποτε ανεβάζω εσύ μου το λύνεις!!
Φιλικά,
Ευθύμης Αλεξίου
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 17466
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: 52 φύλλα της τράπουλας
Το ενδιαφέρον αυτό πρόβλημα είναι αρκετά γνωστό, και ονομάζεται στην βιβλιογραφία "collecting coupons".
Η συνηθισμένη διατύπωσή του είναι:
Αν μαζεύω κουπόνια, όπως για παράδειγμα παλαιότερα σε πακέτα με τσίχλες
υπήρχε η εικόνα ενός ποδοσφαιριστή και ο στόχος ήταν να μαζεύψω όλο το πακέτο,
πόσες κατά μέσο όρο τσίχλες πρέπει να αγοράσω;
Για παράδειγμα θα το βρει κανείς στο βιβλίο του Moesteller, Fifty Challenging Problems
in Probability, εκδόσεις Dover, Πρόβλημα , σελίς
, σελίς  , με λύση στην σελίδα
, με λύση στην σελίδα  .
.
Στην γενική περίπτωση η απάντηση είναι ασυμπτωτικά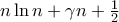 , όπου
, όπου  η
η
σταθερά Euler.
Ήξερα από παλαιότερα την λύση, αλλά δεν την έγραψα για να την χαρεί άλλος. Είχα
πρωτοσυναντήσει το πρόβλημα στα φοιτητικά μου χρόνια, σε μάθημα Πιθανοτήτων και
Στατιστικής, με τον φωτισμένο δάσκαλο D. R. Cox, σπουδαίο Στατιστικό.
Η συνηθισμένη διατύπωσή του είναι:
Αν μαζεύω κουπόνια, όπως για παράδειγμα παλαιότερα σε πακέτα με τσίχλες
υπήρχε η εικόνα ενός ποδοσφαιριστή και ο στόχος ήταν να μαζεύψω όλο το πακέτο,
πόσες κατά μέσο όρο τσίχλες πρέπει να αγοράσω;
Για παράδειγμα θα το βρει κανείς στο βιβλίο του Moesteller, Fifty Challenging Problems
in Probability, εκδόσεις Dover, Πρόβλημα
 , σελίς
, σελίς  , με λύση στην σελίδα
, με λύση στην σελίδα  .
. Στην γενική περίπτωση η απάντηση είναι ασυμπτωτικά
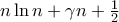 , όπου
, όπου  η
η σταθερά Euler.
Ήξερα από παλαιότερα την λύση, αλλά δεν την έγραψα για να την χαρεί άλλος. Είχα
πρωτοσυναντήσει το πρόβλημα στα φοιτητικά μου χρόνια, σε μάθημα Πιθανοτήτων και
Στατιστικής, με τον φωτισμένο δάσκαλο D. R. Cox, σπουδαίο Στατιστικό.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
