 , η οποία είναι συνεχής και "1-1". Υποθέτουμε ότι ισχύει:
, η οποία είναι συνεχής και "1-1". Υποθέτουμε ότι ισχύει:  και ότι
και ότι 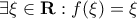 . Ν.δ.ό
. Ν.δ.ό  .
.Στέλιος
Συντονιστές: m.pαpαgrigorakis, Καρδαμίτσης Σπύρος, Πρωτοπαπάς Λευτέρης, R BORIS, KAKABASBASILEIOS, Μπάμπης Στεργίου
 , η οποία είναι συνεχής και "1-1". Υποθέτουμε ότι ισχύει:
, η οποία είναι συνεχής και "1-1". Υποθέτουμε ότι ισχύει:  και ότι
και ότι 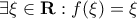 . Ν.δ.ό
. Ν.δ.ό  .
.Γράφω μια πολλή ωραία λύση που μου έστειλε σε προσωπικό e-mail ο φίλος Δημήτρης Μπουνάκης, ένας από τους Συμβούλους Μαθηματικών στη Κρήτη:mostel έγραψε:Θεωρούμε τη συνάρτηση, η οποία είναι συνεχής και "1-1". Υποθέτουμε ότι ισχύει:
και ότι
. Ν.δ.ό
.
 . Χωρίς βλάβη
. Χωρίς βλάβη  . Δύο περιπτώσεις μπορεί να έχουμε: Είτε
. Δύο περιπτώσεις μπορεί να έχουμε: Είτε  είτε
είτε  .
.  και
και  .
.
 είναι φθίνουσα (διότι
είναι φθίνουσα (διότι  άρα
άρα  και όμοια η γενική περίπτωση).
και όμοια η γενική περίπτωση). (διότι
(διότι  και όμοια η γενική περίπτωση).
και όμοια η γενική περίπτωση). (απλό).
(απλό). συγκλίνει. Από την γ) έχουμε
συγκλίνει. Από την γ) έχουμε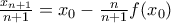
 εργαζόμαστε όμοια αλλά τώρα χρησιμοποιώντας την ισοδύναμη μορφή
εργαζόμαστε όμοια αλλά τώρα χρησιμοποιώντας την ισοδύναμη μορφή  της δοθείσας συναρτησιακής σχέσης.
της δοθείσας συναρτησιακής σχέσης. Κλέβοντας ιδέες από την λύση του Δημήτρη έγραψα αμέσως από πάνω, γράφω μία παραλλαγή της:mostel έγραψε:Θεωρούμε τη συνάρτηση, η οποία είναι συνεχής και "1-1". Υποθέτουμε ότι ισχύει:
και ότι
. Ν.δ.ό
.
 και
και 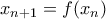 .
.  (η περίπτωση
(η περίπτωση  αντιμετωπίζεται όμοια) εύκολα βλέπουμε επαγωγικά ότι ισχύει
αντιμετωπίζεται όμοια) εύκολα βλέπουμε επαγωγικά ότι ισχύει 
 συγκλίνει.
συγκλίνει.



 .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες