Κάποια μπορoύν να λυθούν με τρόπους που σουλουπώνονται και στα λυκειακά πλαίσια και κάποια άλλα όχι.
Θα συμπληρώνω την εδώ λίστα για να είναι όλα μαζεμένα, αφού το θέματα είναι σχετικά.






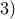
 , (βγαίνει και λυκειακά)
, (βγαίνει και λυκειακά) 

 , (βγαίνει και λυκειακά)
, (βγαίνει και λυκειακά) 
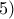
 .
.
 Αν η
Αν η ![f:[0,1]\to\mathbb{R} f:[0,1]\to\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/2f88c23f13b9b1904c39f298cd688669.png) είναι συνεχής και
είναι συνεχής και  , να βρεθεί το όριο
, να βρεθεί το όριο  . (βγαίνει και λυκειακά)
. (βγαίνει και λυκειακά) 
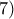
 .
. 

 όπου
όπου  .
. 

 Έστω
Έστω  συνεχής στο
συνεχής στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) και
και  μη σταθερά πολυώνυμα με
μη σταθερά πολυώνυμα με  και με το
και με το  να έχει θετικό μεγιστοβάθμιο συντελεστή.
να έχει θετικό μεγιστοβάθμιο συντελεστή. Ας υπολογισθεί το όριο
 .
.(Αυτή είναι δικό μου μαγείρεμα και γενικεύει το παρακάτω. Ελπίζω να μην έχει γίνει καμμία πατάτα)
 Ας βρεθεί τώρα το όριο
Ας βρεθεί τώρα το όριο  . (Αυτό είναι από το Νεγρεπόντη)
. (Αυτό είναι από το Νεγρεπόντη) 
 Με τις ίδιες προϋποθέσεις όπως και στο
Με τις ίδιες προϋποθέσεις όπως και στο  , ας υπολογισθεί το όριο
, ας υπολογισθεί το όριο .
.(Και αυτή είναι δικό μου μαγείρεμα. Ελπίζω πάλι...).
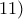

 Τούτο εδώ είναι απολύτως σχετικό με τα προβλήματα που τίθενται
Τούτο εδώ είναι απολύτως σχετικό με τα προβλήματα που τίθενται  εδώ
εδώ εδώ και
εδώ και εδώ.
εδώ.Έστω
![f:[0,1]\to(0,+\infty) f:[0,1]\to(0,+\infty)](/forum/ext/geomar/texintegr/latexrender/pictures/394c72a1d5ea289299f96cd43a87cbb4.png) συνεχής. Δείξτε ότι για κάθε
συνεχής. Δείξτε ότι για κάθε  υπάρχει
υπάρχει  με
με  και υπολογίστε το όριο
και υπολογίστε το όριο  .
.
![\displaystyle{
\int\limits_0^1 {nx(1 - x^2 )^n dx = n\int\limits_0^{\frac{\pi }{2}} {\sin t} (1 - \sin ^2 t)^n \cos tdt = - n\int\limits_0^{\frac{\pi }{2}} {\cos ^{2n + 1} td(\cos t) = - n\left[ {\frac{{\cos ^{2n + 2} t}}{{2n + 2}}} \right]_0^{\frac{\pi }{2}} = \frac{n}{{2n + 2}}} }
} \displaystyle{
\int\limits_0^1 {nx(1 - x^2 )^n dx = n\int\limits_0^{\frac{\pi }{2}} {\sin t} (1 - \sin ^2 t)^n \cos tdt = - n\int\limits_0^{\frac{\pi }{2}} {\cos ^{2n + 1} td(\cos t) = - n\left[ {\frac{{\cos ^{2n + 2} t}}{{2n + 2}}} \right]_0^{\frac{\pi }{2}} = \frac{n}{{2n + 2}}} }
}](/forum/ext/geomar/texintegr/latexrender/pictures/086f1bcbc78b1ea9ce290524655ec12b.png)


 και
και  οπότε το κριτήριο παρεμβολής δε δουλεύει.
οπότε το κριτήριο παρεμβολής δε δουλεύει.
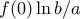
 και ότι ο παρονομαστής είναι πολυώνυμο του
και ότι ο παρονομαστής είναι πολυώνυμο του  βαθμού σίγουρα μεγαλύτερου του 1. Το πρώτο μαζί με το Θεώρημα Κυριαρχημένης Σύγκλισης του Lebesgue μας λέει ότι μπορούμε να εναλλάξουμε όριο και ολοκλήρωμα και το δεύτερο ότι η οριακή συνάρτηση είναι η μηδενική. Άρα το ζητούμενο όριο είναι ολοκλήρωμα της μηδενικής δηλαδή 0.
βαθμού σίγουρα μεγαλύτερου του 1. Το πρώτο μαζί με το Θεώρημα Κυριαρχημένης Σύγκλισης του Lebesgue μας λέει ότι μπορούμε να εναλλάξουμε όριο και ολοκλήρωμα και το δεύτερο ότι η οριακή συνάρτηση είναι η μηδενική. Άρα το ζητούμενο όριο είναι ολοκλήρωμα της μηδενικής δηλαδή 0.
![\displaystyle{
\ln (x + \frac{{x^5 }}{t}) = \ln x + \ln (1 + \frac{{x^4 }}{t}),\forall x \in \left[ {1,2} \right],\forall t > 0
} \displaystyle{
\ln (x + \frac{{x^5 }}{t}) = \ln x + \ln (1 + \frac{{x^4 }}{t}),\forall x \in \left[ {1,2} \right],\forall t > 0
}](/forum/ext/geomar/texintegr/latexrender/pictures/8691f9f9e71655c453d8c0a3b288e6ad.png)

![\displaystyle{
g(x)=1 + \frac{{x^4 }}{t},x \in \left[ {1,2} \right]
} \displaystyle{
g(x)=1 + \frac{{x^4 }}{t},x \in \left[ {1,2} \right]
}](/forum/ext/geomar/texintegr/latexrender/pictures/edee90d8f78bb378b5d19dbfadd7c95e.png)
![\displaystyle{
g(1) \le g(x) \le g(2),\forall x \in \left[ {1,2} \right] \Leftrightarrow 1 + \frac{1}{t} \le 1 + \frac{{x^4 }}{t} \le 1 + \frac{{16}}{t},\forall x \in \left[ {1,2} \right]
} \displaystyle{
g(1) \le g(x) \le g(2),\forall x \in \left[ {1,2} \right] \Leftrightarrow 1 + \frac{1}{t} \le 1 + \frac{{x^4 }}{t} \le 1 + \frac{{16}}{t},\forall x \in \left[ {1,2} \right]
}](/forum/ext/geomar/texintegr/latexrender/pictures/49397780dce5bfba78c76b0d9afaace4.png)
![\displaystyle{
\ln (1 + \frac{1}{t}) \le \ln (1 + \frac{{x^4 }}{t}) \le \ln (1 + \frac{{16}}{t}),\forall x \in \left[ {1,2} \right]
} \displaystyle{
\ln (1 + \frac{1}{t}) \le \ln (1 + \frac{{x^4 }}{t}) \le \ln (1 + \frac{{16}}{t}),\forall x \in \left[ {1,2} \right]
}](/forum/ext/geomar/texintegr/latexrender/pictures/09e9c0dcd39d5e6e53627823ca563f37.png)




![\displaystyle{
\frac{{2x}}{\pi } \le \sin x \le x,x \in \left[ {0,\frac{\pi }{2}} \right]
} \displaystyle{
\frac{{2x}}{\pi } \le \sin x \le x,x \in \left[ {0,\frac{\pi }{2}} \right]
}](/forum/ext/geomar/texintegr/latexrender/pictures/e5459ed957ec7868021ce9ade3247df8.png)


![\displaystyle{
\left[ {\frac{{-e^{ - tx} }}{t}} \right]_0^{\frac{\pi }{2}} \le \int\limits_0^{\frac{\pi }{2}} {e^{ - t\sin x} dx} \le \left[ { - \frac{{e^{ - \frac{{2tx}}{\pi }} }}{{\frac{{2t}}{\pi }}}} \right]_0^{\frac{\pi }{2}}
} \displaystyle{
\left[ {\frac{{-e^{ - tx} }}{t}} \right]_0^{\frac{\pi }{2}} \le \int\limits_0^{\frac{\pi }{2}} {e^{ - t\sin x} dx} \le \left[ { - \frac{{e^{ - \frac{{2tx}}{\pi }} }}{{\frac{{2t}}{\pi }}}} \right]_0^{\frac{\pi }{2}}
}](/forum/ext/geomar/texintegr/latexrender/pictures/09df81eb2677284cacb1ed1fe59e4a42.png)



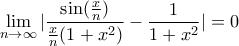

![\displaystyle{
[0,t],t < + \infty
} \displaystyle{
[0,t],t < + \infty
}](/forum/ext/geomar/texintegr/latexrender/pictures/9ca7e7355157d1af804483b218f01055.png)




 για κάποιο
για κάποιο  με
με  .
.  λόγω συνέχειας της
λόγω συνέχειας της  .
. συνεχώς παραγωγίσιμη στο
συνεχώς παραγωγίσιμη στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) , τότε
, τότε για κάποιο
για κάποιο  .
.![f:[a,b] \to \mathbb{R} f:[a,b] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/1e32016b6e720735017fcee010f23652.png) συνεχής. Τότε
συνεχής. Τότε  .
. .
.


 όπου
όπου  και
και  για
για ![x \in (0,1] x \in (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5f3bd0dafa13199e5ec59664dccbce7e.png) .
. μπορεί να υπολογιστεί π.χ. με L' Hopital. (Προσοχή: Το θεωρούμε συνάρτηση του
μπορεί να υπολογιστεί π.χ. με L' Hopital. (Προσοχή: Το θεωρούμε συνάρτηση του  .)
.)![x \in [0,1] x \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) έχουμε
έχουμε  το οποίο είναι ανεξάρτητο του
το οποίο είναι ανεξάρτητο του 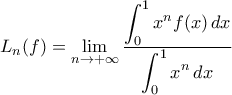 .
.
 για κάθε πολυώνυμο P.
για κάθε πολυώνυμο P.![|f(x)-p(x)|<\epsilon, \forall \epsilon \in [0,1] |f(x)-p(x)|<\epsilon, \forall \epsilon \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5ec39df388ab1b2f688463cf5d7a8e90.png)
 ώστε
ώστε 
 (Ι η I(x)=1)
(Ι η I(x)=1)