socrates έγραψε:ΑΣΚΗΣΗ 412
Να βρείτε τον μικρότερο τετραψήφιο αριθμό

για τον οποίο το σύστημα

έχει ακέραια ρίζα.
Με αφαίρεση κατά μέλη των δύο εξισώσεων που δίνονται, έχουμε:

![\displaystyle{(x+y)^{3}-3xy(x+y)+xy(x+y)-[(x+y)^{2}-2xy]-(x+y)+1=0\Rightarrow} \displaystyle{(x+y)^{3}-3xy(x+y)+xy(x+y)-[(x+y)^{2}-2xy]-(x+y)+1=0\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/10ae6840eb2c9414ee88b03c70fadb7b.png)
![\displaystyle{(x+y)^{3}-2xy(x+y)-[(x+y)^{2}-2xy]-(x+y-1)=0\Rightarrow} \displaystyle{(x+y)^{3}-2xy(x+y)-[(x+y)^{2}-2xy]-(x+y-1)=0\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/54edfac647908e0612ba4681e71d0eb4.png)
![\displaystyle{(x+y)[(x+y)^{2}-2xy]-[(x+y)^{2}-2xy]-(x+y-1)=0\Rightarrow} \displaystyle{(x+y)[(x+y)^{2}-2xy]-[(x+y)^{2}-2xy]-(x+y-1)=0\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/d4b90e432ffe277324f99586307a6073.png)
-(x+y-1)=0\Rightarrow (x+y-1)[(x+y)^{2}-2xy]=0\Rightarrow} \displaystyle{[(x+y)^{2}-2xy](x+y-1)-(x+y-1)=0\Rightarrow (x+y-1)[(x+y)^{2}-2xy]=0\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/91abb40be565a7c498ab4bd6ebb13f81.png)

ή

Αν ήταν

τότε επειδή πρόκειται για ακέραιους, θα έπρεπε


ή αντιστρόφως. Όμως σε όλες αυτές τις περιπτώσεις, ο

δεν θα ήταν τετραψήφιος, που είναι άτοπο. Άρα πρέπει μόνο να εξετάσουμε την περίπτωση

Θεωρούμε λοιπόν το σύστημα


από αυτό παίρνουμε


Άρα


'Αρα τα

είναι οι ρίζες της εξίσωσης:

, δηλαδή της εξίσωσης:

, της οποίας η διακρίνουσα είναι

. Πρέπει όμως η διακρίνουσα να είναι τέλειο τετράγωνο ακεραίου αριθμού. Δηλαδή να υπάρχει

ακέραιος, ώστε να είναι

και άρα

. Για να είναι ο

ακέραιος, πρέπει αρχικά ο

να είναι άρτιος. Δηλαδή να υπάρχει

ακέραιος ώστε

. Τότε έχουμε

και άρα

και για να είναι ακέραιος αυτός πρέπει ο

να είναι περιττός, δηλαδή να υπάρχει

ακέραιος ώστε να είναι

. Τότε έχουμε

Επειδή θέλουμε o

να είναι τετραψήφιος, πρέπει

δηλαδή

και από την ανίσωση αυτή βρίσκουμε ότι

ή

Οπότε διαπιστώνουμε ότι ο ακέραιος

για τον οποίο ο

παίρνει την ελάχιστη τιμή (ως τετραψήφιος) είναι η

οπότε

(ή θα μπορούσαμε ακόμα να παίρναμε την

και πάλι θα είχαμε

)
Συνεπώς η ελάχιστη ακέραια τιμή για τον τετραψήφιο αριθμό

είναι η

η οποία εύκολα βλέπουμε ότι επαληθεύει το σύστημα.
, για τους οποίους ο αριθμός
είναι τετράγωνο ακεραίου.
 ο αριθμός
ο αριθμός  είναι τετράγωνο ακεραίου ενώ για
είναι τετράγωνο ακεραίου ενώ για  κάτι τέτοιο δεν ισχύει.Εξετάζουμε για
κάτι τέτοιο δεν ισχύει.Εξετάζουμε για  και βρίσκουμε:
και βρίσκουμε:  πράγμα που σημαίνει οτι η ρίζα του (1) βρίσκεται μεταξύ δύο φυσικών αριθμών συνεπώς ο (1) δεν είναι τετράγωνο ακεραίου.Στη συνέχεια χρησιμοποιώντας επέκταση του θεωρήματος του Φερμά που λέει οτι:
πράγμα που σημαίνει οτι η ρίζα του (1) βρίσκεται μεταξύ δύο φυσικών αριθμών συνεπώς ο (1) δεν είναι τετράγωνο ακεραίου.Στη συνέχεια χρησιμοποιώντας επέκταση του θεωρήματος του Φερμά που λέει οτι:  μόνο για
μόνο για  όπου
όπου  ,
, ,
,
 καταλήγουμε στο οτι για κάθε
καταλήγουμε στο οτι για κάθε  ο αριθμός(1) ΔΕΝ είναι τετράγωνο ακεραίου.Αρα μόνο για
ο αριθμός(1) ΔΕΝ είναι τετράγωνο ακεραίου.Αρα μόνο για  τηρούνται οι προυποθέσεις της άσκησης.
τηρούνται οι προυποθέσεις της άσκησης.
 λόγω θεωρήματος Φερμά.Έπειτα παρατηρούμε οτι:
λόγω θεωρήματος Φερμά.Έπειτα παρατηρούμε οτι:  που σημαίνει οτι ο αριθμός(2) δεν είναι τετράγωνο ακεραίου,
που σημαίνει οτι ο αριθμός(2) δεν είναι τετράγωνο ακεραίου,  .Είμαι σωστός ή όχι;
.Είμαι σωστός ή όχι; είναι πραγματικοί αριθμοί τέτοιοι ώστε
είναι πραγματικοί αριθμοί τέτοιοι ώστε  και
και  να δείξετε ότι
να δείξετε ότι
 όπου
όπου  είναι μη αρνητικοί. Οπότε αρκεί να δείξουμε ότι:
είναι μη αρνητικοί. Οπότε αρκεί να δείξουμε ότι:




 τέτοια ώστε
τέτοια ώστε 
 συμβολίζουμε το πλήθος των (θετικών) διαιρετών του φυσικού αριθμού
συμβολίζουμε το πλήθος των (θετικών) διαιρετών του φυσικού αριθμού 
 είτε με
είτε με  . Επομένως το αριστερό μέλος είναι ισότιμο με
. Επομένως το αριστερό μέλος είναι ισότιμο με  η
η  ενώ το δεξί με
ενώ το δεξί με  είναι περιττοί. Για κάθε θετικό ακέραιο
είναι περιττοί. Για κάθε θετικό ακέραιο  όμως, μπορούμε να χωρίσουμε τους διαιρέτες του σε ζεύγη της μορφή
όμως, μπορούμε να χωρίσουμε τους διαιρέτες του σε ζεύγη της μορφή  και επομένως το
και επομένως το  είναι άρτιος εκτός και αν το
είναι άρτιος εκτός και αν το  είναι μονοσύνολο.) Επειδή
είναι μονοσύνολο.) Επειδή  για να είναι το
για να είναι το  τέλειο τετράγωνο πρέπει
τέλειο τετράγωνο πρέπει  και άρα
και άρα  . Άρα
. Άρα  και άρα
και άρα  . Δηλαδή το μόνο ζεύγος που ικανοποιεί την συνθήκη είναι το
. Δηλαδή το μόνο ζεύγος που ικανοποιεί την συνθήκη είναι το  .
.

![\displaystyle{(x+y)^{3}-3xy(x+y)+xy(x+y)-[(x+y)^{2}-2xy]-(x+y)+1=0\Rightarrow} \displaystyle{(x+y)^{3}-3xy(x+y)+xy(x+y)-[(x+y)^{2}-2xy]-(x+y)+1=0\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/10ae6840eb2c9414ee88b03c70fadb7b.png)
![\displaystyle{(x+y)^{3}-2xy(x+y)-[(x+y)^{2}-2xy]-(x+y-1)=0\Rightarrow} \displaystyle{(x+y)^{3}-2xy(x+y)-[(x+y)^{2}-2xy]-(x+y-1)=0\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/54edfac647908e0612ba4681e71d0eb4.png)
![\displaystyle{(x+y)[(x+y)^{2}-2xy]-[(x+y)^{2}-2xy]-(x+y-1)=0\Rightarrow} \displaystyle{(x+y)[(x+y)^{2}-2xy]-[(x+y)^{2}-2xy]-(x+y-1)=0\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/d4b90e432ffe277324f99586307a6073.png)
-(x+y-1)=0\Rightarrow (x+y-1)[(x+y)^{2}-2xy]=0\Rightarrow} \displaystyle{[(x+y)^{2}-2xy](x+y-1)-(x+y-1)=0\Rightarrow (x+y-1)[(x+y)^{2}-2xy]=0\Rightarrow}](/forum/ext/geomar/texintegr/latexrender/pictures/91abb40be565a7c498ab4bd6ebb13f81.png)
 ή
ή 

 ή αντιστρόφως. Όμως σε όλες αυτές τις περιπτώσεις, ο
ή αντιστρόφως. Όμως σε όλες αυτές τις περιπτώσεις, ο  δεν θα ήταν τετραψήφιος, που είναι άτοπο. Άρα πρέπει μόνο να εξετάσουμε την περίπτωση
δεν θα ήταν τετραψήφιος, που είναι άτοπο. Άρα πρέπει μόνο να εξετάσουμε την περίπτωση 




 είναι οι ρίζες της εξίσωσης:
είναι οι ρίζες της εξίσωσης:  , δηλαδή της εξίσωσης:
, δηλαδή της εξίσωσης:  , της οποίας η διακρίνουσα είναι
, της οποίας η διακρίνουσα είναι  . Πρέπει όμως η διακρίνουσα να είναι τέλειο τετράγωνο ακεραίου αριθμού. Δηλαδή να υπάρχει
. Πρέπει όμως η διακρίνουσα να είναι τέλειο τετράγωνο ακεραίου αριθμού. Δηλαδή να υπάρχει  και άρα
και άρα  . Για να είναι ο
. Για να είναι ο  ακέραιος ώστε
ακέραιος ώστε  . Τότε έχουμε
. Τότε έχουμε  και άρα
και άρα  και για να είναι ακέραιος αυτός πρέπει ο
και για να είναι ακέραιος αυτός πρέπει ο  ακέραιος ώστε να είναι
ακέραιος ώστε να είναι  . Τότε έχουμε
. Τότε έχουμε 
 δηλαδή
δηλαδή  και από την ανίσωση αυτή βρίσκουμε ότι
και από την ανίσωση αυτή βρίσκουμε ότι 

 οπότε
οπότε  (ή θα μπορούσαμε ακόμα να παίρναμε την
(ή θα μπορούσαμε ακόμα να παίρναμε την  και πάλι θα είχαμε
και πάλι θα είχαμε  να γράφεται ως γινόμενο (δύο ή περισσότερων) διαδοχικών ακεραίων.
να γράφεται ως γινόμενο (δύο ή περισσότερων) διαδοχικών ακεραίων. πραγματικοί, τέτοιοι ώστε να ισχύει
πραγματικοί, τέτοιοι ώστε να ισχύει  και
και  να αποδείξετε ότι
να αποδείξετε ότι  για κάθε θετικό ακέραιο
για κάθε θετικό ακέραιο 
 και τέτοιοι ώστε:
και τέτοιοι ώστε:
 και
και  να δείξετε ότι:
να δείξετε ότι: 
 και με μήκη πλευρών ακέραιοι αριθμοί.
και με μήκη πλευρών ακέραιοι αριθμοί. θετικούς πραγματικούς, με
θετικούς πραγματικούς, με  και
και  να δειχθεί ότι:
να δειχθεί ότι:
 πραγματικοί αριθμοί τέτοιοι ώστε
πραγματικοί αριθμοί τέτοιοι ώστε  να δείξετε ότι
να δείξετε ότι 
 πλευράς
πλευράς  και
και  σημεία των
σημεία των  ώστε
ώστε  . Να δειχθεί ότι
. Να δειχθεί ότι
 . 'Έστω ότι η μια από τις κοινές αυτές εφαπτομένες τέμνει τον μικρό κύκλο στο σημείο
. 'Έστω ότι η μια από τις κοινές αυτές εφαπτομένες τέμνει τον μικρό κύκλο στο σημείο  και τον μεγάλο στο
και τον μεγάλο στο  . Αν
. Αν  , να υπολογίσετε το εμβαδόν του μικρού κύκλου.
, να υπολογίσετε το εμβαδόν του μικρού κύκλου. ,
,  σημείο της
σημείο της  και
και  το μέσον της
το μέσον της  . Η
. Η  τέμνει την
τέμνει την  στο
στο  και η
και η  την
την  στο
στο  .
. (
(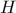 σημείο της
σημείο της  (
(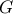 σημείο της
σημείο της  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. . Φέρνουμε ευθεία
. Φέρνουμε ευθεία  έτσι ώστε η γωνία
έτσι ώστε η γωνία  να είναι ίση με
να είναι ίση με  . Από τα
. Από τα  και
και  συναρτήσει του
συναρτήσει του  .
. θεωρούμε δύο χορδές
θεωρούμε δύο χορδές  που είναι κάθετες μεταξύ τους και δεν περνάνε από το κέντρο του κύκλου. Οι δύο χορδές τέμνονται στο σημείο
που είναι κάθετες μεταξύ τους και δεν περνάνε από το κέντρο του κύκλου. Οι δύο χορδές τέμνονται στο σημείο  , έτσι ώστε να είναι
, έτσι ώστε να είναι  . Έστω
. Έστω  το συμμετρικό του
το συμμετρικό του 
 θεωρούμε σημείο
θεωρούμε σημείο  και
και  να είναι ίσες.
να είναι ίσες.
 βρίσκονται ο ένας εκτός του άλλου. Να βρεθεί :
βρίσκονται ο ένας εκτός του άλλου. Να βρεθεί : είναι τέλειο τετράγωνο ακεραίου.
είναι τέλειο τετράγωνο ακεραίου.  το πλήθος των ρόμβων πλευράς 1, που σχηματίζονται.
το πλήθος των ρόμβων πλευράς 1, που σχηματίζονται.  είναι πρώτος αριθμός.
είναι πρώτος αριθμός. και
και  οι κάθετες πλευρές ορθογωνίου τριγώνου τότε ισχύει:
οι κάθετες πλευρές ορθογωνίου τριγώνου τότε ισχύει:  όπου
όπου  η υποτείνουσά του.Στον Ευκλείδιο χώρο το θεώρημα γίνεται:
η υποτείνουσά του.Στον Ευκλείδιο χώρο το θεώρημα γίνεται:  όπου
όπου  οι χωρικές διαστάσεις(μήκος,πλάτος,βάθος).2.Από το θεώρημα του Φερμά,γνωρίζουμε οτι ΔΕΝ ισχύει:
οι χωρικές διαστάσεις(μήκος,πλάτος,βάθος).2.Από το θεώρημα του Φερμά,γνωρίζουμε οτι ΔΕΝ ισχύει:  για
για 
 και
και  όπου
όπου  .Θέτουμε τώρα
.Θέτουμε τώρα  και καταλήγουμε:
και καταλήγουμε:  που σημαίνει οτι ο αριθμός κάτω από τη ρίζα δεν ειναι τετράγωνο ακεραίου.Στη συνέχεια θέτουμε:
που σημαίνει οτι ο αριθμός κάτω από τη ρίζα δεν ειναι τετράγωνο ακεραίου.Στη συνέχεια θέτουμε:  και παρατηρούμε οτι η σχέση (1) είναι (σχεδόν) ίδια με τη σχέση (3).Αφού η (1) δε μας <<οδήγησε>> σε τέλειο τετράγωνο τότε ούτε η (3) και συνεπώς ούτε η (2) μας <<οδηγούν>> σε παρόμοιο συμπέρασμα.Καταλήγουμε με επαγωγή,οτι για κάθε
και παρατηρούμε οτι η σχέση (1) είναι (σχεδόν) ίδια με τη σχέση (3).Αφού η (1) δε μας <<οδήγησε>> σε τέλειο τετράγωνο τότε ούτε η (3) και συνεπώς ούτε η (2) μας <<οδηγούν>> σε παρόμοιο συμπέρασμα.Καταλήγουμε με επαγωγή,οτι για κάθε  ο αριθμός
ο αριθμός  δεν είναι τετράγωνο ακεραίου.ΠΑΡΑΤΗΡΗΣΗ:Βάζοντας
δεν είναι τετράγωνο ακεραίου.ΠΑΡΑΤΗΡΗΣΗ:Βάζοντας  και
και  στη (1) καθώς και
στη (1) καθώς και  και
και  στη (2),καταλήγουμε (με επαγωγή και πάλι) στο συμπέρασμα οτι κάθε φορά που καταλήγουμε στη σχέση:
στη (2),καταλήγουμε (με επαγωγή και πάλι) στο συμπέρασμα οτι κάθε φορά που καταλήγουμε στη σχέση:  ο αριθμός στη μέση των ανισώσεων,δεν είναι τετράγωνο ακεραίου.Παίρνουμε τώρα τις σχέσεις:
ο αριθμός στη μέση των ανισώσεων,δεν είναι τετράγωνο ακεραίου.Παίρνουμε τώρα τις σχέσεις:  και
και  .Παρατηρούμε οτι και οι δύο σχέσεις γράφονται κατα τα πρότυπα της (4): η (5) για
.Παρατηρούμε οτι και οι δύο σχέσεις γράφονται κατα τα πρότυπα της (4): η (5) για  και
και  ενώ η (6) για
ενώ η (6) για  και
και  .Άρα οι αριθμοί
.Άρα οι αριθμοί  και
και  δεν είναι τετράγωνα ακεραίων.Με επαγωγή,βρίσκουμε οτι για κάθε
δεν είναι τετράγωνα ακεραίων.Με επαγωγή,βρίσκουμε οτι για κάθε  ο αριθμός
ο αριθμός  (δεν την έχω).Η μόνη λύση πάντως της άσκησης είναι για
(δεν την έχω).Η μόνη λύση πάντως της άσκησης είναι για  .ΔΕΙΤΕ ΤΗΝ ΠΑΡΑΚΑΤΩ ΔΗΜΟΣΙΕΥΣΗ.
.ΔΕΙΤΕ ΤΗΝ ΠΑΡΑΚΑΤΩ ΔΗΜΟΣΙΕΥΣΗ. έχουμε π.χ. την
έχουμε π.χ. την  . Ακόμη όμως και αν εννοείς
. Ακόμη όμως και αν εννοείς  τότε πάλι υπάρχει πρόβλημα. Ο Euler είχε εικάσει ότι δεν υπάρχουν ακέραιοι
τότε πάλι υπάρχει πρόβλημα. Ο Euler είχε εικάσει ότι δεν υπάρχουν ακέραιοι  ώστε
ώστε  αλλά η εικασία αποδείχθηκε λανθασμένη. Ένα παράδειγμα είναι το
αλλά η εικασία αποδείχθηκε λανθασμένη. Ένα παράδειγμα είναι το  . Περισσότερα
. Περισσότερα 
 για τους οποίους ορίζονται τα κλάσματα.
για τους οποίους ορίζονται τα κλάσματα. 
 και ο αριθμός
και ο αριθμός  είναι τέλειο τετράγωνο ακεραίου, να δείξετε ότι
είναι τέλειο τετράγωνο ακεραίου, να δείξετε ότι 

 τέτοιοι ώστε
τέτοιοι ώστε 
 έτσι ώστε
έτσι ώστε 
 σημεία στο επίπεδο έτσι ώστε:
σημεία στο επίπεδο έτσι ώστε: και
και από αυτά τα σημεία στο εξωτερικό του;
από αυτά τα σημεία στο εξωτερικό του;


 έχουμε
έχουμε








 ,,, ΣΧΕΣΗ (1)
,,, ΣΧΕΣΗ (1) είναι άρρητος.
είναι άρρητος. ρητός τέτοιος ώστε να είναι
ρητός τέτοιος ώστε να είναι 

 τότε η σχέση αυτή καταλήγει σε άτοπο. Άρα το δεύτερο μέλος είναι άρρητος ενώ το πρώτο ρητός. Συνεπώς δείξαμε ότι ο αριθμός
τότε η σχέση αυτή καταλήγει σε άτοπο. Άρα το δεύτερο μέλος είναι άρρητος ενώ το πρώτο ρητός. Συνεπώς δείξαμε ότι ο αριθμός  είναι άρρητος, οπότε από την ΣΧΕΣΗ (1) έχουμε:
είναι άρρητος, οπότε από την ΣΧΕΣΗ (1) έχουμε: και
και  από όπου προκύπτει ότι
από όπου προκύπτει ότι  και
και 
 , οπότε
, οπότε  αλλά δεν είναι αλήθεια ότι ο αριθμός κάτω από τη ρίζα (δηλαδή ο
αλλά δεν είναι αλήθεια ότι ο αριθμός κάτω από τη ρίζα (δηλαδή ο  ), δεν είναι τετράγωνο ακεραίου.
), δεν είναι τετράγωνο ακεραίου.  . Άρα
. Άρα  . Αρκεί λοιπόν να αποδείξουμε ότι:
. Αρκεί λοιπόν να αποδείξουμε ότι:


 ,,,,(ΣΧΕΣΗ 1)
,,,,(ΣΧΕΣΗ 1)

 , από την υπόθεση και
, από την υπόθεση και προφανώς αφού
προφανώς αφού 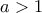 . Άρα
. Άρα και έτσι η ΣΧΕΣΗ 1 είναι αληθής άρα έχουμε και το ζητούμενο.
και έτσι η ΣΧΕΣΗ 1 είναι αληθής άρα έχουμε και το ζητούμενο.




 που να είναι τέτοιοι ώστε:
που να είναι τέτοιοι ώστε:


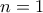 τότε θα έίχαμε
τότε θα έίχαμε  που όμως είναι αδύνατον.Έπομένως με
που όμως είναι αδύνατον.Έπομένως με 
![\displaystyle{m-1=\frac{8}{n-1}\Rightarrow (m-1)(n-1)=8\Rightarrow [m-1=1, & , n-1=8]} \displaystyle{m-1=\frac{8}{n-1}\Rightarrow (m-1)(n-1)=8\Rightarrow [m-1=1, & , n-1=8]}](/forum/ext/geomar/texintegr/latexrender/pictures/fc51e2609ba8c5d57982a7540bce2567.png) ή
ή ![\displaystyle{[m-1=2 , & , n-1=4]} \displaystyle{[m-1=2 , & , n-1=4]}](/forum/ext/geomar/texintegr/latexrender/pictures/adc77f224531ff469f36e2ae7d13d43a.png)
 ή όταν είναι
ή όταν είναι  , τότε το κλάσμα παίρνει την ίδια ρητή τιμή και το ίδιο συμβαίνει και όταν το
, τότε το κλάσμα παίρνει την ίδια ρητή τιμή και το ίδιο συμβαίνει και όταν το  και
και  .
.  στοιχεία του συνόλου, τα δύο από αυτά θα είναι ίδια με δύο άλλα. Απο αυτά συμπεραίνουμε ότι το σύνολο περιέχει
στοιχεία του συνόλου, τα δύο από αυτά θα είναι ίδια με δύο άλλα. Απο αυτά συμπεραίνουμε ότι το σύνολο περιέχει  στοιχεία,
στοιχεία,

 τότε η πιο πάνω σχέση κκαταλήγει σε άτοπο, αφού θα είχαμε ρητός = άρρητος
τότε η πιο πάνω σχέση κκαταλήγει σε άτοπο, αφού θα είχαμε ρητός = άρρητος , οπότε τότε θα είναι υποχρεωτικά και
, οπότε τότε θα είναι υποχρεωτικά και  . Από αυτές τις δύο εξισώσεις, παίρνουμε ότι:
. Από αυτές τις δύο εξισώσεις, παίρνουμε ότι:


 που είναι άτοπο. Άρα δεν υπάρχουν ρητοί αριθμοί που να ικανοποιούν την δοσμένη σχέση.
που είναι άτοπο. Άρα δεν υπάρχουν ρητοί αριθμοί που να ικανοποιούν την δοσμένη σχέση.